Лоґіт-нормальний розподіл
| Лоґіт-нормальний | |
|---|---|
 | |
Функція розподілу ймовірностей 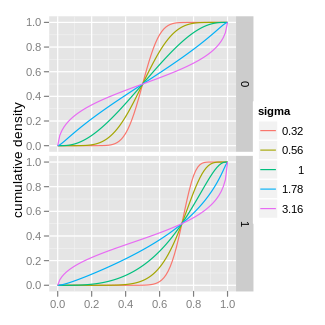 | |
| Параметри | σ2 > 0 — квадрат параметра шкали (дійсне), μ ∈ R — параметр локації |
| Носій функції | x ∈ (0, 1) |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | немає аналітичного вираження |
| Медіана | |
| Мода | немає аналітичного вираження |
| Дисперсія | немає аналітичного вираження |
| Твірна функція моментів (mgf) | немає аналітичного вираження |
У теорії ймовірностей лоґіт-нормальний розподіл — це розподіл ймовірностей випадкової величини, лоґіт якого має нормальний розподіл. Якщо Y — випадкова величина з нормальним розподілом, а t — стандартна логістична функція, то X=t (Y) має лоґіт-нормальний розподіл; так само, якщо X має лоґіт-нормальний розподіл, то має нормальний розподіл. Він також відомий як лоґістичний нормальний розподіл[1], який часто відноситься до поліноміальної лоґіт-версії (наприклад див. [2][3]).
Змінну можна змоделювати як лоґіт-нормальною випадковою величиною, якщо це пропорція, яка обмежена нулем і одиницею, і де значення нуль і одиниця ніколи не зустрічаються.
Функція щільності ймовірності (PDF) лоґіт-нормального розподілу для 0 < x < 1:
де μ і σ є середнім і стандартним відхиленням лоґіту змінної (за визначенням, лоґіт змінної є нормально розподіленим).
Щільність, отримана шляхом зміни знака μ, є симетричною, оскільки вона дорівнює f(1-x;- μ, σ), зсуваючи моду в інший бік 0,5 (середина інтервалу (0,1)).
Моменти лоґіт-нормального розподілу не мають аналітичного розв’язку. Моменти можна оцінити чисельним інтегруванням, однак числове інтегрування може бути непомірним, коли значення такі, що функція густини розбіжна до нескінченності в кінцевих точках нуль і один. Альтернативою є використання спостереження, що лоґіт-нормаль є перетворенням нормальної випадкової змінної. Це дозволяє нам наблизити -й момент через наступну квазіоцінку Монте-Карло
де стандартна логістична функція, і є оберненою кумулятивною функцією розподілу нормального розподілу із середнім і дисперсією .

Коли похідна густини дорівнює 0, то положення моди x задовольняє таке рівняння:
Для деяких значень параметрів існує два розвʼязки, тобто розподіл є бімодальним.
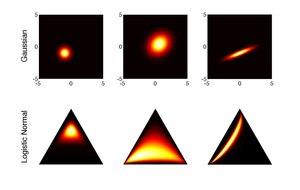
Логістичний нормальний розподіл є узагальненням лоґіт-нормального розподілу у D-вимірні вектори ймовірностей шляхом логістичного перетворення багатовимірного нормального розподілу[1][4][5].
де позначає вектор перших (D-1) компонентів і позначає симплекс D-вимірних векторів ймовірностей. Застосування адитивного логістичного перетворення для відображення багатовимірної нормальної випадкової змінної до симплексу дає:
Унікальне обернене відображення задається:
- .
Це випадок вектора x, сума компонентів якого дорівнює одиниці. У випадку х із сигмоїдальними елементами, тобто коли
отримаємо
де логарифмування і ділення аргументів здійснюється поелементно. Це забезпечується тим, що матриця Якобі перетворення є діагональною з елементами .
Логістичний нормальний розподіл є більш гнучкою альтернативою розподілу Діріхле, оскільки він може фіксувати кореляції між компонентами векторів ймовірностей. Він також має потенціал для спрощення статистичного аналізу композиційних даних, дозволяючи відповідати на запитання про логарифмічні співвідношення компонентів векторів даних. Часто цікавлять в практичних задачах досліджують співвідношення, а не абсолютні значення компонентів.
Симплекс ймовірностей є обмеженим простором, що робить стандартні методи, які зазвичай застосовуються до векторів у менш значущими. Ейтчісон описав проблему несправжніх відʼємних кореляцій при застосуванні таких методів безпосередньо до симплексних векторів[4]. Однак відображення композиційних даних в шляхом зворотного адитивного логістичного перетворення дає дійснозначні дані в . До цього представлення даних можна застосувати стандартні методи. Цей підхід виправдовує використання лоґіт-нормального розподілу, який, отже, можна розглядати як «Ґаусівський симплекс».

Розподіл Діріхле та логіт-нормальний розподіл ніколи не є абсолютно рівними для будь-якого вибору параметрів. Однак Ейчісон описав метод апроксимації Діріхле з логістичною нормаллю, щоб їх розбіжність Кульбака–Лейблера (KL) була мінімімальна:
Мінімум набувається при:
Використовуючи властивості моментів розподілу Діріхле, розв’язок можна записати через дигамму і тригамма функції:
Це наближення особливо точне для великих . Фактично, можна показати, що для , маємо.
- Бета-розподіл і розподіл Кумарасвамі, інші двопараметричні розподіли на обмеженому інтервалі з подібними формами
- ↑ а б Aitchison, J.; Shen, S. M. (1980). Logistic-normal distributions: Some properties and uses. Biometrika. 67 (2): 261. doi:10.2307/2335470. ISSN 0006-3444. JSTOR 2335470.
- ↑ Peter Hoff, 2003. Link
- ↑ Log-normal and logistic-normal terminology - AI and Social Science – Brendan O'Connor. brenocon.com. Процитовано 18 квітня 2018.
- ↑ а б J. Atchison. "The Statistical Analysis of Compositional Data." Monographs on Statistics and Applied Probability, Chapman and Hall, 1986. Book
- ↑ Hinde, John (2011). Logistic Normal Distribution. У Lovric, Miodrag (ред.). International Encyclopedia of Statistical Sciences. Springer. с. 754—755. doi:10.1007/978-3-642-04898-2_342. ISBN 978-3-642-04897-5.
- Frederic, P. & Lad, F. (2008) Two Moments of the Logitnormal Distribution. Communications in Statistics-Simulation and Computation. 37: 1263-1269 (англ.)
- Mead, R. (1965). A Generalised Logit-Normal Distribution. Biometrics. 21 (3): 721—732. doi:10.2307/2528553. JSTOR 2528553. PMID 5858101. (англ.)
- logitnorm package for R


![{\displaystyle {\frac {1}{2}}{\Big [}1+\operatorname {erf} {\Big (}{\frac {\operatorname {logit} (x)-\mu }{\sqrt {2\sigma ^{2}}}}{\Big )}{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f866d537580a7e284ff45c5b6ba44282405d5437)





![{\displaystyle E[X^{n}]\approx {\frac {1}{K-1}}\sum _{i=1}^{K-1}\left(P\left(\Phi _{\mu ,\sigma ^{2}}^{-1}(i/K)\right)\right)^{n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f6194558f091fda796896edd4b1cb390fbf201)








![{\displaystyle \mathbf {x} =\left[{\frac {e^{y_{1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},\dots ,{\frac {e^{y_{D-1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},{\frac {1}{1+\sum _{i=1}^{D-1}e^{y_{i}}}}\right]^{\top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d9c97b2fcf6aa03dd19a3bd83b6ff96f2deb7f7)
![{\displaystyle \mathbf {y} =\left[\log \left({\frac {x_{1}}{x_{D}}}\right),\dots ,\log \left({\frac {x_{D-1}}{x_{D}}}\right)\right]^{\top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd6953a8dc1335421fa50d4956fe959f724590a5)
![{\displaystyle \mathbf {y} =\left[\log \left({\frac {x_{1}}{1-x_{1}}}\right),\dots ,\log \left({\frac {x_{D}}{1-x_{D}}}\right)\right]^{\top }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41624f2bfd185e5111e9d4ec2339495bf420d3ff)





![{\displaystyle {\boldsymbol {\mu }}^{*}=\mathbf {E} _{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]\quad ,\quad {\boldsymbol {\Sigma }}^{*}={\textbf {Var}}_{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b35a2ca21cc73c82be7e6e40e22cc8e3e297d36e)







