Множення матриць

Множе́ння ма́триць — це бінарна операція, яка використовуючи дві матриці, утворює нову матрицю, яка називається доб́утком ма́триць. Дійсні або комплексні числа множаться відповідно до правил елементарної арифметики.
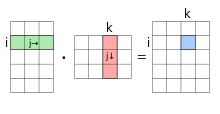
Схема праворуч демонструє обчислення добутку двох матриць A і B. Вона показує як перетини в добутку матриць відповідають рядкам матриці A і стовпцям матриці B. Значення на перетинах відмічених кружечками будуть:
Окрім загально відомого, існують і інші види множення матриць. Ключовими особливостями будь-якого матричного множення є: кількість рядків і стовпців, в початкових матрицях, і правило, як елементи матриць утворюють нову матрицю.

Нехай дано дві прямокутні матриці розміру та розміру :
Тоді матриця розмірністю називається їх добутком:
де:
Операція множення двох матриць здійсненна тільки в тому випадку, якщо число стовпців в першому співмножнику дорівнює числу рядків у другому; в цьому випадку говорять, що форма матриць узгоджена. Зокрема, множення завжди здійснимо, якщо обидва множники — квадратні матриці одного і того ж порядку.
Слід зауважити, що з існування добутку зовсім не випливає існування добутку


Добуток матриць AB складається з усіх можливих комбінацій скалярних добутків вектор-рядків матриці A і вектор-стовпців матриці B. Елемент матриці AB з індексами i, j є скалярним добутком i-го вектор-рядка матриці A і j-го вектор-стовпця матриці B.
У загальному випадку, добуток матриць не є комутативною операцією. Приміром:
Елемент добутку матриць приведених вище, обчислюється таким чином
Перша координата в позначенні матриці позначає рядок, друга координата — стовпець; цей порядок використовують як при індексації, так і при позначенні розміру. Елемент на перетині рядка та стовпця результуючої матриці є скалярним добутком -го рядка першої матриці і -го стовпця другої матриці. Це пояснює чому ширина і висота множимих матриць повинні збігатися: інакше скалярний добуток не визначено.


Описане правило матричного множення прозоріше всього мотивується, виходячи з множення вектора на матрицю.
Останнє звичайно вводиться виходячи з того, що при розкладанні векторів по базису дію (кожного) лінійного оператора A дає вираз компонент вектора v' = Av:
Тобто лінійний оператор виявляється представлений матрицею, вектори — векторами-стовпцями, а дія оператора на вектор — матричним множенням вектора-стовпця зліва на матрицю оператора (це окремий випадок матричного множення, коли одна з матриць — вектор-стовпець — має розмір 1хn).
(Так само перехід до будь-якого нового базису при зміні координат представляється повністю аналогічним виразом, тільки в цьому випадку вже не компоненти нового вектора в старому базисі, а компоненти старого вектора в новому базисі; при цьому — елементи матриці переходу до нового базису).
Розглянувши послідовну дію на вектор двох операторів: спочатку A, а потім B (або перетворення базису A, а потім перетворення базису B), двічі застосувавши формулу, отримуємо:
звідки видно, що композиції BA дії лінійних операторів A і B (або аналогічної композиції перетворень базису) відповідає матриця, що обчислюється за правилом добутку відповідних матриць:
Визначений таким чином добуток матриць виявляється абсолютно звичайним і очевидно корисним (дає простий і універсальний спосіб обчислення композицій довільної кількості лінійних перетворень).
Сполучна властивість, асоціативність:
Розподільна властивість, дистрибутивність щодо додавання:
- .
Добуток матриці на одиничну матрицю того ж порядку дорівнює самій матриці:
Добуток матриці на нульову матрицю тієї ж розмірності дорівнює нульовий матриці:
Якщо і — квадратні матриці одного і того ж порядку, то добуток матриць має ще ряд властивостей.
Множення матриць в загальному випадку є некомутативним:
Якщо , то матриці і називаються перестановочними або комутуючими між собою.
Найпростіші приклади комутуючих матриць:
- будь-яка квадратна матриця — з самою собою: (зведення матриці в квадрат);
- будь-яка квадратна матриця — з одиничною матрицею того ж порядку: ;
- будь-яка квадратна матриця — з нульовою матрицею того ж порядку: ;
- будь-яка невироджена квадратна матриця — зі своєю зворотною матрицею: .
Визначник і слід добутку не залежать від порядку множення матриць:
Ранг добутку не перевищує рангу кожного з множників
Квадратна матриця називається неособливою(невиродженою), якщо вона має єдину обернену матрицю таку, що виконується умова:
Інакше матриця називається особливою (виродженою).
Матриця порядку є невиродженою в тому і лише в тому випадку, якщо в цьому випадку є квадратна матриця того ж порядку
де — алгебраїчне доповнення елементу у визначнику
Складність обчислення добутку матриць за визначенням становить , однак існують більш ефективні алгоритми[1], що застосовуються для великих матриць. Питання про граничну швидкість множення великих матриць, також як і питання про побудову найбільш швидких і стійких практичних алгоритмів множення великих матриць залишається однією з невирішених проблем лінійної алгебри.
- Алгоритм Штрассена (1969): Перший алгоритм швидкого множення великих матриць був розроблений Фолькером Штрассеном[2] в 1969. В основі алгоритму лежить рекурсивне розбиття матриць на блоки 2Х2. Штрассен довів, що матриці 2Х2 можна некомутативно перемножити за допомогою семи множень, тому на кожному етапі рекурсії виконується сім множень замість восьми. В результаті асимптотична складність цього алгоритму складає . Недоліком даного методу є велика складність програмування в порівнянні зі стандартним алгоритмом, слабка чисельна стійкість і більший обсяг використовуваної пам'яті. Розроблено ряд алгоритмів на основі методу Штрассена, які покращують чисельну стійкість, швидкість по константі і інші його характеристики. Проте, в силу простоти алгоритм Штрассена залишається одним з практичних алгоритмів множення великих матриць. Штрассен також висунув наступну гіпотезу Штрассена: для як завгодно малого існує алгоритм, що при досить великих натуральних n гарантує перемножування двох матриць розміру за операцій.
- Подальші поліпшення показника ступеня ω для швидкості матричного множення

- Надалі оцінки швидкості множення великих матриць багаторазово поліпшувалися. Однак ці алгоритми носили теоретичний, в основному наближений характер. В силу нестійкості алгоритмів наближеного множення в даний час вони не використовуються на практиці.
- Алгоритм Пана (1978)
- У 1978 Пан[3] запропонував свій метод множення матриць, складність якого склала Θ(n2.78041).
- Алгоритм Біні (1979)
- У 1979 група італійських учених на чолі з Біні[4] розробила алгоритм множення матриць з використанням тензорів. Його складність становить Θ(n2.7799).
- Алгоритми Шенхаге (1981)
- У 1981 Шенхаге[5] представив метод, який працює зі швидкістю Θ(n2.695). Оцінка отримана за допомогою підходу, названого частковим матричним множенням. Пізніше йому вдалося отримати оцінку Θ(n2.6087).
- Потім Шенхаге на базі методу прямих сум отримав оцінку складності Θ(n2.548). Романі зумів понизити оцінку до Θ(n2.5166), а Пан — до Θ(n2.5161).
- У 1990 Копперсміт і Віноград[en][6] опублікували алгоритм, який в модифікації Вильямс Василевської[7] 2011 року перемножує матриці зі швидкістю O(n2.3727). Цей алгоритм використовує ідеї, схожі з алгоритмом Штрассена. На сьогоднішній день модифікації алгоритму Копперсміта-Винограда є найбільш асимптотично швидкими. Але той факт, що отримані поліпшення нікчемні, дозволяє говорити про існування «бар'єру Копперсміта-Винограда» в асимптотичних оцінках швидкості алгоритмів. Алгоритм Копперсміта-Винограда ефективний тільки на матрицях астрономічного розміру і на практиці застосовуватися не може.
- Зв'язок з теорією груп (2003)
- У 2003 Кох та ін. розглянули в своїх роботах[8] алгоритми Штрассена і Копперсміта-Винограда в контексті теорії груп. Вони показали, що гіпотеза Штрассена справедлива, якщо виконується одна з гіпотез теорії груп[9].
- Скелетний розклад матриці — розклад на 2 прямокутні множники мінімального рангу.
- Розклад матриці — представлення у вигляді добутку 2 чи 3 матриць більш простої структури.
- Гантмахер Ф. Р. Теорія матриць. — 2025. — 757 с.(укр.)
- Ланкастер П.. Теория матриц. — 2. — Москва : Наука, 1982. — 272 с.(рос.)
- Р.Хорн, Ч.Джонсон. Матричный анализ. — М: : Мир, 1989. — 653 с.(рос.)
- Gene H. Golub, Charles F. Van Loan. Matrix Computations. — 4. — М: : The Johns Hopkins University Press, 2013. — 756 с.(англ.)
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — Москва : Наука, 1973. — 832 с.(рос.)
- ↑ Кібернетичний збірник. Нова серія. Вип. 25. Сб. статей 1983–1985 рр .: Пер. з англ. — М .: Мир, 1988 — В. Б. Алексєєв. Складність множення матриць. Огляд.
- ↑ Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354–356, 1969
- ↑ Pan V. Ya, Strassen's algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations. — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
- ↑ Bini D., Capovani M., Lotti G., Romani F. — complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
- ↑ Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251-280, 1990.
- ↑ Williams, Virginia (2011), Multiplying matices in O(n2.3727 time [Архівовано 26 жовтня 2014 у Wayback Machine.]
- ↑ Group-theoretic Algorithms for Matrix Multiplication (PDF). Архів оригіналу (PDF) за 6 серпня 2011. Процитовано 26 жовтня 2014.
- ↑ Toward an Optimal Algorithm for Matrix Multiplication (PDF). Архів оригіналу (PDF) за 31 березня 2010. Процитовано 26 жовтня 2014.

















































![{\displaystyle A=\left[a_{ik}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a01bb07c21110e6da874868082f2529ab616d070)

![{\displaystyle \det A=\det \left[a_{ik}\right]\neq 0;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94de2af97d80f9a3716cc7c115bfd303e550d869)

![{\displaystyle A^{-1}=\left[a_{ik}\right]^{-1}=\left[{\frac {A_{ki}}{\det A}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/728e599f82952094ff4fd506edd088dac1f03ff3)


![{\displaystyle \det \left[a_{ik}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee0470c90d16ae67c8c58ae2f2854741f59b156)





