Модулярна ґратка

Модулярна ґратка — ґратка, яка задовольняє наступний самодвоїстий закон:
- із слідує ,
де ≤ є відношення нестрогого порядку, ∨ та ∧ (бінарні операції об'єднання та перетину). Модулярні ґратки природно виникають в алгебрі та в багатьох інших галузях математики. Наприклад, підмножини векторного простору (модуль над кільцем) утворюють модулярні ґратки.
Кожна дистрибутивна ґратка є модулярною.
Не обов'язково в модулярній ґратці може бути елемент b, модульний закон виконується для довільного елемента a та x (≤ b). Такий елемент називається модулярним елементом. Загалом, модульний закон може існувати для фіксованої пари (a, b). Така пара називається модулярною парою.
Модулярний закон можна спостерігати як обмежений асоціативний закон, який з'єднує дві операції:
- λ(μx) = (λμ)x.
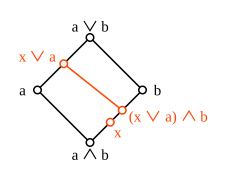
Модулярний закон:
- x ≤ b слідує x ∨ (a ∧ b) ≥ (x ∨ a) ∧ b.
Підставляючи замість x вираз x ∧ b, модульний закон може бути виражений у вигляді рівняння наступним чином:
- (x ∧ b) ∨ (a ∧ b) = [(x ∧ b) ∨ a] ∧ b.
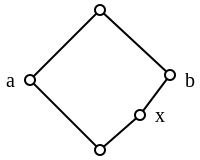
Це показує, що, використовуючи термінологію з універсальної алгебри, модулярні ґратки утворюють різноманіття решіток. Найменша немодулярна ґратка — це «Пентагон»(N5), що складається з п'яти елементів 0,1,x,a,b, таких що
- 0 < x < b < 1, 0 < a < 1.
Для цієї ґратки справедливо:
- x ∨ (a ∧ b) = x ∨ 0 = x < b = 1 ∧ b = (x ∨ a) ∧ b, що суперечить модульному закону.
Кожна немодулярна ґратка містить копію N5.
Модулярні ґратки іноді називають дедекіндовими структурами на честь Ріхарда Дедекінда, який відкрив модулярні ідентичності.
Для будь-яких двох елементів a,b модулярної ґратки, можна розглядати інтервали [a ∧ b, b] та [a, a ∨ b]. Вони пов'язані та зберігають порядок:
- φ: [a ∧ b, b] → [a, a ∨ b] та
- ψ: [a, a ∨ b] → [a ∧ b, b]
які визначаються φ(x) = x ∨ a та ψ(x) = x ∧ b.
-
В модулярній ґратці, відображення φ і ψ, що вказані стрілками є взаємно зворотним ізоморфізмом.
-
Суперечність теоремі ізоморфізму алмазів в немодулярній ґратці.
Композиція ψφ зберігає порядок відображення на інтервалі [a ∧ b, b] та задовольняє нерівності ψ(φ(x)) = (x ∨ a) ∧ b ≥ x. Аналогічно φψ тотожно [a, a ∨ b]. Отже спостерігаємо ізоморфізм двох відображень φ та ψ.
Цей результат іноді називають теоремою алмазів ізоморфізму для модулярних ґраток. Ґратка є модулярною тоді і тільки тоді, коли теорема алмазів ізоморфізму існує для будь-якої пари елементів.
Теорема алмазів ізоморфізму для модулярних ґраток аналогічна третій теоремі про ізоморфізми в алгебрі.

У будь-якій ґратці, модулярна пара являє собою пару ( a, b ) елементів, таких що для всіх х виконується a ∧ b ≤ x ≤ b, то (x ∨ a) ∧ b = x. Елемент b ґратки називається правим модулярним елементом, якщо (a, b ) являє собою модулярну пару для всіх елементів a.
Ґратка має властивість таку що, якщо (a, b) являє собою модулярну пару, то ( b, a ) також є модулярною парою, та називається M-симетричною ґраткою. У ґратках N5 , описаних вище, пара ( b, a ) є модульною, але пари (a, b) немає. Тому N5 не є M-симетричною. Центрова ґратка шестикутника S7 М-симетрична, але не модулярна. З того, що N5 є підґраткою S7 випливає, що M-симетричні ґратки не утворюють різноманіття ґраток.
M-симетрія не є поняттям самодвоїстості. Двоїсті модулярні пари являють собою пару, яка має подвійне відношення порядку, а ґратка називається двоїстою M-симетричною або M*-симетричною (подвійна M-симетричність ). Отже ґратка може бути модулярною тоді й тільки тоді, коли вона M-симетрична і M*-симетрична. Це еквівалентно і для нескінченних ґраток, які задовольняють умову максимальності (або низхідний ланцюжковий стан).
Ґратки навхрест симетричні тоді, коли для кожної модулярної пари ( a, b ) пара ( b, a ) є двічі модулярною. Симетрія навхрест означає, що виконується M-симетрія, але не виконується M*-симетрія. Тому вона не еквівалентна подвійній симетрії навхрест. Ґратка з найменшим елементом 0 є ⊥-симетричною, якщо для кожної модулярної пари ( a, b ), що задовольняє a ∧ b = 0, пара (b, a) також є модулярною.
Термін «модулярність» пов'язаний з ім’ям німецького математика Ріхарда Дедекінда. Він опублікував велику частину документів після його виходу на пенсію. У статті, опублікованій в 1894 році, він вивчав ґратки, які назвав подвійними групами (нім. Dualgruppen). Він також зазначив, що для ґраток загалом модулярний закон є еквівалентним двоїстому.
Дедекінд також зазначив, що будь-яка ґратка комутативного кільця задовольняє наступній формі модулярної ідентичності, яка також є самодвоїстою:
- (x ∧ b) ∨ (a ∧ b) = [x ∨ a] ∧ b.
Він називав ґратки, які задовольняють цій тотожності, подвійною групою ідеального типу (нім. Dualgruppen vom Idealtypus). У сучасній літературі їх частіше називають дистрибутивними ґратками.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
- Corry, Leo, Modern algebra and the rise of mathematical structures (вид. 2nd), с. 121—129, ISBN 978-3-7643-7002-2
- Dedekind, Richard (1897), Ueber Zerlegungen von Zahlen durch ihre grössten gemeinsamen Teiler, Braunschweiger Festschrift: 1—40
- Dedekind, Richard (1900), Ueber die von drei Moduln erzeugte Dualgruppe, Mathematische Annalen, 53 (3): 371—403, doi:10.1007/BF01448979
- Fofanova, T. S. (2001), lattice Semi-modular lattice, у Hazewinkel, Michiel (ред.), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
- Maeda, Shûichirô (1965), On the symmetry of the modular relation in atomic lattices, Journal of Science of the Hiroshima University, 29: 165—170
- Rota, Gian-Carlo (1997), The many lives of lattice theory (PDF), Notices of the American Mathematical Society, 44 (11): 1440—1445, ISSN 0002-9920
- Skornyakov, L. A. (2001), lattice Modular lattice, у Hazewinkel, Michiel (ред.), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
- Stern, Manfred (1999), Semimodular lattices, Cambridge University Press, ISBN 978-0-521-46105-4