Векторний простір
| Алгебричні структури |
|---|
Ве́кторний (ліні́йний) про́стір — основне поняття лінійної алгебри, узагальнення множини всіх векторів на площині чи в просторі з операціями додавання векторів та множення вектора на скаляр.
Прикладом векторного простору є Евклідові вектори. Вони відображають фізичні величини такі як сили: будь-які дві сили (однакової природи) можна додавати між собою і отримати в результаті третю, а множення вектору сили на дійсний множник дає інший вектор сили. Аналогічним чином, але в більш геометричному сенсі, вектори що відображають переміщення в площині або у тривимірному просторі також утворюють векторні простори. Вектори у векторному просторі не обов'язково повинні бути об'єктами у вигляді стрілок, як їх часто наведено в прикладах: вектори слід розглядати як абстрактні математичні об'єкти із певними властивостями, які в деяких випадках можна зобразити у вигляді направлених відрізків (стрілок).
Елементи лінійного простору називаються векторами, але не робиться ніяких припущень стосовно природи чи походження цих елементів. Наприклад, у функціональному аналізі розглядаються топологічні векторні простори, утворені з функцій однієї чи кількох змінних, а вектори стану в квантовій механіці описують стан квантової системи. Матриці заданого розміру також утворюють векторний простір. Зміст наведених нижче аксіом полягає у тому, що незалежно від природи елементів векторного простору, їхнє додавання і множення на скаляр задовольняють правила «шкільної алгебри».
У довільному векторному просторі не визначені операції скалярного, векторного добутку; норми чи метрики. Ці операції можуть вводитись як додаткові структури. Проте векторні простори із скалярним або ермітовим скалярним добутком відіграють важливу роль як у лінійній алгебрі, так і поза її межами, див. напр. гільбертів простір.
Поняття векторного простору можна спершу пояснити за допомогою двох окремих прикладів:
У першому прикладі векторний простір складається із «стрілок» на площині, що беруть початок із однієї фіксованої точки, що є початком відліку. У фізиці їх використовують аби описати сили або швидкості. Нехай дано дві такі стрілки, v і w, і паралелограм, що утворений двома цими направленими відрізками містить діагональ, що бере початок з тієї ж точки. Ця нова побудована стрілка є сумою двох попередніх стрілок — v + w. В особливому випадку коли стрілки знаходяться на одній прямій, їхньою сумою буде стрілка на цій прямій, довжина якої дорівнювати сумі або різниці довжин, і залежності від того чи мали стрілки однаковий напрям чи ні. Іншою операцією яку можна виконати над стрілками є масштабування: для будь-якого даного додатного дійсного числа a, стрілка що має такий самий напрямок як v, але його довжина збільшена або зменшена множенням на a, називається добутком вектора v на скаляр a. Він позначається як av. Якщо a від'ємне, av результатом буде стрілка, що вказує в протилежному напрямку.
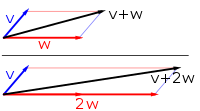
На наступних зображеннях наведено два приклади: якщо a = 2, результуючий вектор aw має спільний напрямок із w, але збільшену вдвічі довжину відносно w (зображення праворуч знизу). Аналогічно, 2w є сумою w + w. Крім того, (−1)v = −v має протилежний напрям і однакову довжину з v (вектор, що вказує вниз і показаний синім на зображенні праворуч).
-
Додавання векторів: сума v + w (чорним) векторів v (синім) і w (червоним).
-
Скалярний добуток: множення −v і 2w.
У другому ключовому прикладі векторний простір задано парами дійсних чисел x і y. (Важливим є порядок входження компонент x і y, тому така пара ще називається впорядкованою парою.) Записується вона наступним чином — (x, y). Сума двох таких пар і множення пари чисел на число визначатиметься таким чином:
- (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2)
і
- a (x, y) = (ax, ay).
Перший приклад зводиться до даного прикладу, якщо направлені відрізки буде представлено парою декартових координат їх кінцевих точок.
Лінійний простір над полем — це множина елементи якої називаються векторами, у якій визначені:
- бінарна операція додавання векторів:
- унарна операція множення вектора на скаляр:
що задовільняють наступну систему аксіом[1]:
- — комутативна група відносно операції додавання векторів:
- (комутативність додавання)
- (асоціативність додавання)
- (існування нульового вектора)
- (існування протилежного вектора)
- асоціативність та унітарність множення на скаляри:
- (асоціативність множення на скаляри)
- (де це одиниця поля )
- дистрибутивність додавання і множення на скаляр:
Найпоширеніші лінійні простори над полем дійсних чисел або комплексних чисел.
- Основними поняттями в лінійному просторі є: лінійна незалежність векторів, базис, підпростір.
- Пізніше за векторний простір було введено загальніше поняття модуля над кільцем, у визначенні якого поле замінено на кільце . Але в лінійній алгебрі воно не розглядається через проблеми з існуванням базиса.
Векторні простори беруть початок із афінної геометрії після запровадження координат на площині і в тривимірному просторі. Приблизно в 1636, Декарт і Ферма започатковують аналітичну геометрію, коли починають вирішувати рівняння із двома змінними, що є точками на кривій в площині.[2] В 1804, аби отримати геометричні рішення без використання координат, Больцано запропонував певні операції над точками, прямими і площинами, що були попередниками векторів.[3] Його роботу згодом використав Мебіус в 1827 при введені поняття барицентричних координат.[4] В 1828 Мурей[en] припустив існування алгебри, що перевершує не тільки звичайну алгебру, але також і двовимірну алгебру, яку він створив в пошуках геометричної інтерпретації комплексних чисел.[5]
Визначення векторів було засновано на понятті пари точок (англ. bipoint) Беллавітіса, що є орієнтованим сегментом, в якому один кінець є початком, а другий ціллю. Згодом його було опрацьовано Арганом і Гамільтоном із представленням у вигляді Комплексних чисел і згодом при введені понять кватерніонів і бікватерніонів.[6] Вони є елементами у R2, R4, і R8; ставлення до них як до лінійних комбінацій ввів Едмон Лагерр ще у 1867, який також дав визначення системам лінійних рівнянь.
В 1857, Артур Кейлі запропонував матричну нотацію, що дозволяє гармонізувати та спростити лінійні перетворення. Близько в той самий час, Герман Грассман вивчав барицентричні розрахунки, які започаткував Мебіус. Він уявляв множини із абстрактних об'єктів, над якими виконувалися операції.[7] В його роботі фігурували поняття лінійної незалежності і розмірність, а також скалярний добуток. Першим хто дав сучасне визначення векторному простору і лінійним відображенням в 1888 р. був Джузеппе Пеано.[8]
Важливим фактором розвитку векторних просторів була побудова Лебегом функціональних просторів. Близько 1920 це поняття формалізували Стефан Банах і Давид Гільберт.[9] В той час, алгебра почала взаємодіяти із новою областю - функціональним аналізом, зокрема, за допомогою таких ключових понять як простір p-інтегрованих функцій і Гільбертіві простори.[10] Векторні простори, в тому числі нескінченно-вимірні, стали тоді добре вкоріненим поняттям, і багато галузей математики почали використовувати його.

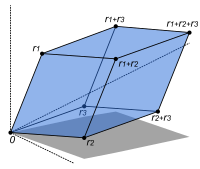
Різні базиси дозволяють задати вектор за допомогою послідовності скалярів, що називаються координатами або компонентами вектора. Базис це (скінченна або нескінченна) множина B = {bi}i ∈ I векторів bi, для зручності вона часто може індексуватися за допомогою деякої множини індексів I, що охоплює весь простір і є лінійно незалежним. Під поширенням на весь простір розуміють, що будь-який вектор v можна задати як скінченну суму (що називається лінійною комбінацією) із базових елементів:
-
(1)
де ak це скаляри, що називаються координатами (або компонентами) вектора v відповідно до базису B, і bik (k = 1, ..., n) елементів із B. Під лінійною незалежністю розуміють, що координати ak є однозначно визначені для будь-якого вектору у векторному просторі.
Наприклад, вектори координат e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), до en = (0, 0, ..., 0, 1), утворюють базис із Fn, що називається стандартним базисом, оскільки будь-який вектор (x1, x2, ..., xn) може бути унікально представлений як лінійна комбінація цих векторів:
- (x1, x2, ..., xn) = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
Відповідні координати x1, x2, ..., xn є декартовими координатами вектора.
Кожен векторний простір має базис. Це випливає із леми Цорна, що є еквівалентним формулюванням Аксіоми вибору.[11] У інші аксіомах із теорії множин Цермело — Френкеля, існування базису також еквівалентне аксіомі вибору.[12] лема про ультрафільтр, що є слабшою за аксіому вибору, покладається на те, що всі вектори векторного простору мають однакову кількість елементів, або потужність (див. Теорема про вимір векторних просторів[en]).[13] Це називають розмірністю векторного простору. Якщо простір складається із нескінченної множини векторів, вищезгадане твердження можливо довести без настільки фундаментального введення в теорію множин.[14]
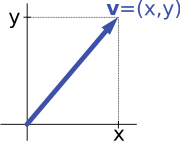
Співвідношення двох векторних просторів можна задати за допомогою лінійного відображення або лінійного перетворення. Це такі функції, які відображають структуру векторного простору — тобто, вони зберігають суми і скалярний добуток:
- f(x + y) = f(x) + f(y) і f(a · x) = a · f(x) для всіх x і y в V, всіх a в F.[15]
Ізоморфізм — лінійне відображення f : V → W для якого існує обернене відображення g : W → V, що є таким відображенням, для якого дві можливі композиції f ∘ g : W → W і g ∘ f : V → V є тотожними відображеннями. Відповідно, f буде одночасно ін'єкцією і сюр'єкцією.[16] Якщо існує ізоморфізм між V і W, ці два простори називають ізоморфними; тоді по суті як векторні простори вони будуть ідентичними, оскільки всі тотожності, що виконуються для V за допомогою f, перетворюються на подібні в W, і навпаки, за допомогою g.
Наприклад, якщо векторні простори «направлених відрізків на площині» і «впорядкованих пар чисел» є ізоморфними: направлений відрізок v на площині, що виходить із початку координат деякої (фіксованої) системи координат можна задати за допомогою впорядкованої пари x- і y-компонент, як показано на малюнку праворуч. І навпаки, для даної пари (x, y), напрям відрізку праворуч (або ліворуч, якщо x є від'ємним) буде задавати значення x , а y — вгору (вниз, якщо y є від'ємним), що дозволяє повернутися назад до направленого відрізку v.

Матриці є зручною нотацію, для описання лінійних відображень.[17] Вони записуються у вигляді впорядкованого прямокутного масиву скалярів як показано на малюнку праворуч. Будь-яка матриця A розміром m-на-n збільшує лінійне відображення із Fn до Fm, наступним чином
- , де позначає суму, або, використовуючи матричне множення матриці A на вектор координат x:
- x ↦ Ax.
Крім того, якщо обрати базиси для V і W, будь-яке лінійне відображення f : V → W однозначно можна задати за допомогою цього рівняння.[18]
Детермінант det (A) квадратної матриці A є скаляром, який вказує чи є це відображення ізоморфізмом чи ні: аби це було так достатньо і необхідно аби детермінант не дорівнював нулю.[19] Лінійне перетворення Rn, що відповідає дійсній матриці n-на-n зберігає орієнтацію тоді і лише тоді, коли детермінант є додатнім.
- ↑ А. И. Кострикин, Ю. И. Манин. Линейная алгебра и геометрия.
- ↑ Bourbaki 1969, ch. "Algèbre linéaire et algèbre multilinéaire", pp. 78–91
- ↑ Bolzano 1804
- ↑ Möbius 1827
- ↑ Crowe, Michel J. (1994), A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, Dover, с. 11 and 16, ISBN 0-486-67910-1
- ↑ Hamilton 1853
- ↑ Grassmann 1844
- ↑ Peano 1888, ch. IX
- ↑ Banach 1922
- ↑ Dorier 1995, Moore 1995
- ↑ Roman 2005, Theorem 1.9, p. 43
- ↑ Blass 1984
- ↑ Halpern 1966, pp. 670–673
- ↑ Artin 1991, Theorem 3.3.13
- ↑ Roman 2005, ch. 2, p. 45
- ↑ Lang 1987, ch. IV.4, Corollary, p. 106
- ↑ Lang 1987, ch. V.1
- ↑ Lang 1987, ch. V.3., Corollary, p. 106
- ↑ Lang 1987, Theorem VII.9.8, p. 198
- Гельфанд І. М. Лекції з лінійної алгебри. — 2025. — 248 с.(укр.)
- Гантмахер Ф. Р. Теорія матриць. — 2025. — 757 с.(укр.)
- Банах С. Курс функціонального аналізу (лінійні операції). — К. : Радянська школа, 1948. — 216 с.(укр.)
- Березанський Ю. М., Ус Г. Ф., Шефтель З. Г. Функціональний аналіз : [укр.] = Functional Analysis, Vol. I, Kyiv : Institute of Mathematics, 2010. : [пер. з англ.] : підручник. — Л. : Видавець Чижиков І. Е., 2014. — С. 559. — (Університетська бібліотека). — ISBN 978-966-2645-12-5.
- Ляшко І.І., Ємельянов В.Ф., Боярчук О.К. Математичний аналіз. Частина 1. — К. : Вища школа, 1992. — 496 с. — ISBN 5-11-003757-4.(укр.)
























