Мангеттенська метрика

У Мангеттенській метриці довжини червоної, жовтої і синьої ліній рівні між собою (12). У геометрії Евкліда зелена лінія має довжину 12/√2 ≈ 8.48 і являє собою єдиний найкоротший шлях.

Мангеттенська метрика (метрика прямокутного міста, метрика L₁) — метрика, запроваджена Германом Мінковським. За цією метрикою, відстань між двома точками дорівнює сумі модулів різниць їх координат.

У цієї метрики багато назв. Мангеттенська метрика відома як мангеттенська відстань, відстань міських кварталів, метрика прямокутного міста, метрика L1, вулична метрика або норма $\ell _{1}$ (див. простір L^p), метрика міського кварталу, метрика таксі, прямокутна метрика, метрика прямого кута; на $\mathbb {Z} ^{2}$ її називають метрикою гріди та 4-метрикою.

Назва «мангеттенська відстань» пов'язана з вуличним плануванням Мангеттена, де вулиці перетинаються під прямими кутами.

Кола в дискретній і неперервній геометрії міських кварталів.

Формальне визначення

Мангеттенська метрика $d_{1}$ між двома векторами $\mathbf {p} ,\mathbf {q}$ в n-вимірному дійсному просторі з заданою прямокутною системою координат — сума довжин проєкцій відрізка між точками на осі координат. Більш формально

$d_{1}(\mathbf {p} ,\mathbf {q} )=\|\mathbf {p} -\mathbf {q} \|_{1}=\sum _{i=1}^{n}|p_{i}-q_{i}|,$

де

$\mathbf {p} =(p_{1},p_{2},\dots ,p_{n})$ і $\mathbf {q} =(q_{1},q_{2},\dots ,q_{n})\,$ — вектори.

Наприклад, на площині відстань міських кварталів між точками $(p_{1},p_{2})$ і $(q_{1},q_{2})$ дорівнює $|p_{1}-q_{1}|+|p_{2}-q_{2}|.$

Властивості

Мангеттенська відстань залежить від обертання системи координат, але не залежить від відбиття відносно осі координат або паралельного перенесення. В геометрії, заснованій на мангеттенській метриці, виконуються всі аксіоми Гільберта, окрім аксіоми про конгруентні трикутники.

Куля в цій метриці має форму октаедру, вершини якого лежать на осях координат.

Приклади

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Мангеттенська відстань між двома полями шахової дошки дорівнює мінімальній кількості ходів, яке необхідне візиру, щоб з одного поля перейти в інше.

Відстань в шахах

Відстань між полями шахової дошки для візиру (або тури, якщо відстань рахувати в клітинах) дорівнює мангеттенській відстані; король і ферзь користуються відстанню Чебишова, а слон — мангеттенською відстанню на дошці, повернутій на 45°.

П'ятнашки

Сума мангеттенських відстаней між кісточками і позиціями, в яких вони знаходяться у вирішеній головоломці «П'ятнашки», використовується як евристична функція для пошуку оптимального вирішення.

Клітинні автомати

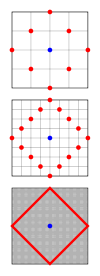
Множина клітин на двовимірному квадратному паркеті, мангеттенська відстань до яких від даної клітини не перевищує r, називається околом фон Неймана діапазону (радіуса) r.

Див. також

• Нормований простір
• Метрика
• Відстань Геммінга
• Відстань Чебишова
• Французька залізнична метрика
• П'ятнашки
• Випадкове блукання

Література

• Eugene F. Krause (1987). Taxicab Geometry. Dover. ISBN 0-486-25202-7.

Посилання

• city-block metric [Архівовано 1 липня 2007 у Wayback Machine.] on PlanetMath
• Weisstein, Eric W. Taxicab Metric(англ.) на сайті Wolfram MathWorld.
• Manhattan distance [Архівовано 12 листопада 2006 у Wayback Machine.]. Paul E. Black, Dictionary of Algorithms and Data Structures [Архівовано 24 червня 2005 у Wayback Machine.], NIST
• Taxi! [Архівовано 19 липня 2008 у Wayback Machine.] — AMS column about Taxicab geometry
• TaxicabGeometry.net — a website dedicated to taxicab geometry research and information