Проєктивний модуль
Зовнішній вигляд
Проєктивний модуль — важливий тип модулів, що є узагальненням вільних модулів. З точки зору теорії категорій, проєктивні модулі є окремим випадком проєктивних об'єктів.
Проєктивний модуль можна визначити кількома еквівалентними способами.
- Модуль над кільцем (як правило, вважається асоціативним з одиничним елементом), називається проєктивним, якщо для будь-якого гомоморфізма і епіморфізма існує такий гомоморфізм , що , тобто дана діаграма є комутативною:
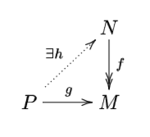
- Модуль є проєктивним тоді і тільки тоді, коли існує такий модуль , що пряма сума є вільним модулем.
- Справді, нехай є компонентою прямої суми , яка є вільним модулем, і — гомоморфізм, a — епіморфізм. Тоді теж є гомоморфізмом ( — проєкція прямої суми на перший доданок ), а так як вільні модулі є проєктивними, то існує гомоморфізм , такий, що , звідси , де — гомоморфізм включення , звідси
- Справді, нехай є компонентою прямої суми , яка є вільним модулем, і — гомоморфізм, a — епіморфізм. Тоді теж є гомоморфізмом ( — проєкція прямої суми на перший доданок ), а так як вільні модулі є проєктивними, то існує гомоморфізм , такий, що , звідси , де — гомоморфізм включення , звідси
- Навпаки, нехай — проєктивний модуль. Кожен модуль є гомоморфним образом вільного. Нехай — відповідний епіморфізм. Тоді тотожний ізоморфізм буде рівним для деякого , так як є проєктивним. Будь-який елемент тоді можна записати як
- ,
- де є ізоморфним .
- Навпаки, нехай — проєктивний модуль. Кожен модуль є гомоморфним образом вільного. Нехай — відповідний епіморфізм. Тоді тотожний ізоморфізм буде рівним для деякого , так як є проєктивним. Будь-який елемент тоді можна записати як
- є проєктивним тоді і тільки тоді, коли для будь-якого епіморфізма індукований гомоморфізм теж є епіморфізмом.
- є проєктивним тоді і тільки тоді, коли він переводить будь-яку коротку точну послідовність в точну послідовність .
- Модуль є проєктивним тоді і тільки тоді, коли кожна коротка точна послідовність модулів виду
- розщеплюється. Тобто для відображення f : B ↠ P на діаграмі існує відображення h : P → B, таке що f ∘ h = idP. У цьому випадку h(P) є прямим доданком модуля B, h є ізоморфізмом із P на h(P), а h ∘ f є проєкцією на h(P). Це також можна записати як
- Модуль над кільцем є проєктивним тоді і тільки тоді, коли існує множина і множина гомоморфізмів таких що для кожного виконується рівність і fi(x) не рівне нулю лише для скінченної кількості індексів i.
- Модуль над кільцем є проєктивним тоді і тільки тоді, коли для всіх R-модулів T функтор Ext задовольняє умову (і тому )
- Пряма сума модулів є проєктивним модулем тоді і тільки тоді, коли кожен доданок є проєктивним.
- Будь-який проєктивний модуль над кільцем головних ідеалів або локальним комутативним кільцем є вільним модулем.
- Будь-який проєктивний модуль є плоским.
- Локалізація проєктивного модуля над комутативним кільцем є проєктивним модулем над локалізованим кільцем. Оскільки проєктивний модуль над локальним кільцем є вільним то локалізація кільця модуля по всіх простих ідеалах є вільним модулем. Також ця властивість описується так, що проєктивний модуль є локально вільним.
- Найпростіший приклад проєктивного модуля — вільний модуль .
- Справді, нехай — елементи базису модуля і . Оскільки — епіморфізм, можна знайти такі , що . Тоді можна визначити, задавши його значення на векторах базису як .
- Для кілець многочленів від кількох змінних над полем будь-який проєктивний модуль є вільним.
- У кільці Дедекінда кожен ідеал, що не є головним є проєктивним модулем і не є вільним модулем.
- Абелева група є проєктивним модулем тоді і тільки тоді, коли вона є вільною.
- Ленг С. Алгебра. — Москва : Мир, 1968. — 564 с. — ISBN 5458320840.(рос.)









































