Робота (фізика)
| робота | ||||
| Бейсбольний гравець виконує роботу над м'ячем, прикладаючи до нього силу протягом руху того у руці. | ||||
| Символи: | A або W | |||
|---|---|---|---|---|
| Одиниці вимірювання | ||||
| SI | 1 Дж = 1 Н·м | |||
| СГС | 1 ерг = 1 г⋅см2⋅с−2 | |||
| У базових величинах SI: | 1 кг⋅м2⋅с−2 | |||
| Розмірність: | M L2 T−2 | |||
|
| ||||
| Класична механіка |
|---|
| Історія класичної механіки |
Робо́та у фізиці — скалярна фізична величина, що характеризує перетворення енергії одного виду на інший, яке відбувається в даній фізичній системі.
У механіці робота (механічна робота) — є мірою дії сили і залежить від величини, напряму цієї сили та переміщення точки її прикладання тобто вона визначає енергетичні витрати на переміщення фізичного тіла, чи його деформацію. Поняття «робота» широко застосовують також у термодинаміці та інших розділах фізики і у техніці.
Робота зазвичай позначається латинською літерою A (від нім. Arbeit), в англомовній літературі — W (від англ. Work), і має розмірність енергії. У системі SI робота вимірюється в джоулях, у системі СГС — у ергах.
При малому переміщенні фізичного тіла під дією сили говорять, що над тілом здійснюється робота
- ,
де — кут між напрямком сили й напрямком переміщення.
Згідно з цією формулою роботу здійснює тільки складник сили, що паралельний переміщенню. Сила, яка перпендикулярна переміщенню, роботи не здійснює.
У випадку, коли тіло рухається по криволінійному контуру C, для знаходження роботи потрібно проінтегрувати наведений вище вираз вздовж контуру:
Якщо сила потенціальна, то робота залежить лише від різниці значень потенціалу в початковій і кінцевій точках і не залежить від форми траєкторії, по якій тіло рухалося між цими двома точками.
У термодинаміці при зміні об'єму тіла на величину під дією тиску над тілом виконується робота
- .
Давньогрецьке розуміння фізики обмежувалося статикою простих механізмів (рівновагою сил) і не включало динаміку чи поняття роботи. В епоху Відродження динаміку механічних сил, як називали прості механізми, почали вивчати з точки зору того, наскільки високо вони можуть підняти вантаж, на додаток до сили, яку вони можуть розвинути, що зрештою привело до нової концепції механічної роботи. Повну динамічну теорію простих механізмів розробив 1600 року італійський учений Галілео Галілей у праці Про механіку (Le Meccaniche), в якій він показав математичну подібність машин як підсилювачів сили.[1][2] Галілей першим пояснив, що прості механізми не створюють енергію, а лише перетворюють її.[1]
Хоча термін робота не використовували до 1826 року, подібні концепції існували й раніше. Це саме поняття називали момент дії, кількість дії, прихована жива сила, динамічний ефект, ефективність і навіть сила.[3] 1637 року французький філософ Рене Декарт писав:[4]
Підняти 100 фунтів на один фут двічі – це те ж саме, що підняти 200 фунтів на один фут або 100 фунтів на два фути.— Рене Декарт, Лист до Гюйгенса
1686 року німецький філософ Готфрід Лейбніц писав:[5]
Однакова сила [«робота» за сучасною термінологією] необхідна, щоб підняти тіло A вагою 1 фунт (libra) на висоту 4 ярди (ulnae), як і для підняття тіла B вагою 4 фунти на висоту 1 ярд.— Готфрід Лейбніц, Brevis demonstratio
1759 року Джон Смітон описав величину, яку він назвав «потужністю» «для позначення напруги сили, гравітації, імпульсу або тиску, щоб викликати рух» (англ. to signify the exertion of strength, gravitation, impulse, or pressure, as to produce motion). Смітон продовжує, що цю величину можна обчислити, якщо «підняту вагу помножити на висоту, на яку її можна підняти за певний час», що робить це визначення надзвичайно схожим на визначення Коріоліса.[6]
Термін робота (або механічна робота) і використання принципу роботи-енергії в механіці започаткували наприкінці 1820-х років незалежно французький математик Гаспар-Гюстав Коріоліс і французький професор прикладної механіки Жан-Віктор Понселе.[7][8][9] Обидва вчені дотримувалися механічного підходу, придатного для вивчення динаміки та потужності машин, наприклад, парових двигунів, які піднімають відра з водою із затоплених рудних шахт. За словами Рене Дюґа[fr], французького інженера та історика, «ми завдячуємо терміном „робота“ в тому значенні, в якому він зараз використовується в механіці» Соломону де Косу[en].[10] Поняття віртуальної роботи та використання варіаційних методів у механіці передувало введенню поняття «механічна робота», але спочатку мало назву «віртуальний момент». Його перейменовано із прийняттям термінології Понселе й Коріоліса.[11][12]
Одиницею роботи в SI є джоуль (Дж), названий на честь англійського фізика Джеймса Прескотта Джоуля (1818—1889), визначений як робота, яку виконує сила 1 Н під час переміщення на 1 м у напрямку сили.
Іноді як одиницю вимірювання роботи використовують розмірнісно еквівалентний ньютон-метр (Н⋅м), але його можна сплутати з одиницею вимірювання моменту сили. Генеральна конференція мір і ваг не рекомендує використовувати Н⋅м, оскільки це може призвести до плутанини щодо того, чи величина, виражена в ньютон-метрах, характеризує момент сили, чи роботу.[13]
Іншою одиницею вимірювання роботи є фут-фунт[en], який походить із англійської системи мір. Як видно з назви одиниці, це добуток фунта як одиниці сили та фут як одиниці переміщення. Один джоуль приблизно дорівнює 0,7376 фут-фунтів.[14][15]
До одиниць роботи, що не належать до SI, належать ньютон-метр, ерг, фут-фунт, фут-паундаль[en], кіловат-година, літр-атмосфера та кінська сила-година[en]. Оскільки робота вимірюється в тих самих одиницях, що й кількість теплоти, іноді для роботи використовують одиниці вимірювання, зазвичай застосвувані для кількості теплоти або енергії, такі як терм[en], британська теплова одиниця і калорія.
Робота A виконана постійною силою величини F над точкою, яка здійснила переміщення s в напрямі дії сили, дорівнює добутку
Наприклад, якщо сила 10 ньютонів (F = 10 Н) діє на точку, яка проходить 2 метри (s = 2 м), тоді A = Fs = (10 Н) (2 м) = 20 Дж. Це приблизно дорівнює роботі проти сили тяжіння, яку виконує людина, щоб підняти над головою від рівня землі тіло масою 1 кг.
Робота подвоюється, якщо підняти подвійний вантаж на ту саму висоту, або підяти той самий вантаж на вдвічі більшу висоту.
Робота тісно пов'язана з енергією. Енергія має ту саму одиницю вимірювання, що й робота (джоуль), оскільки енергія від тіла, яке виконує роботу, передається іншим тілам, з якими воно взаємодіє під час виконання роботи.[15] Принцип роботи-енергії стверджує, що збільшення кінетичної енергії твердого тіла дорівнює величині додатної роботи рівнодійної сил, що діють на це тіло. І навпаки, зменшення кінетичної енергії дорівнює рівній за величиною від'ємній роботі рівнодійної сил, що діють на тіло. Таким чином, якщо сумарна робота додатна, то кінетична енергія тіла збільшується на величину роботи. Якщо сумарна виконана робота від'ємна, то кінетична енергія тіла зменшується на величину роботи.[16]
З другого закону Ньютона можна показати, що робота над вільним (без полів), твердим (без внутрішніх ступенів вільності) тілом дорівнює зміні кінетичної енергії K, що відповідає лінійній швидкості та кутовій швидкості цього тіла, Робота сил, породжена потенціальною функцією, відома як потенціальна енергія, а сили називають консервативними. Отже, робота над тілом, яке переміщується в полі консервативних сил без зміни швидкості чи обертання, дорівнює взятій із протилежним знаком зміні потенціальної енергії U тіла, Ці формули показують, що робота дорівнює енергії, пов'язаній із дією сили, тому робота має фізичну розмірність та одиниці енергії.
Розглянутий принципи роботи/енергії ідентичний принципу електричної роботи/енергії.
Сили реакції визначають можливі переміщення тіла в системі, певним чином обмежуючи його. Наприклад, на похилій площині під дією сили тяжіння тіло притискається до поверхні, а тіло, надягнуте на натягнуту струну, не може рухатися перпендикулярно до неї, щоб зробити струну «натягнутішою».
У механічній системі[17] в'язі унеможливлюють рух у напрямках сил реакції. Отже, віртуальна робота сил реакції дорівнює нулю. Це виконується лише за відсутності сил тертя.[18]
Незмінні сили реакції без тертя не виконують роботи над системою[19] оскільки кут між напрямами руху і сили реакції завжди становить 90°.[19] Прикладами в'язей без виконання роботи є: жорсткі взаємозв'язки між частинками, ковзання по поверхні без тертя та кочення без ковзання.[20]
Наприклад, у системі шківів, як-от машина Атвуда, внутрішні сили між мотузкою та опорним шківом не виконують роботи в системі. Тому роботу обчислюють лише для сил тяжіння, які діють на тіла. Іншим прикладом є доцентрова сила, яка діє на кульку до центра вздовж нитки і змушує її рівномірно рухатися по колу, обмежуючи її рух від центра кола. Ця сила виконує нульову роботу, оскільки вона перпендикулярна до швидкості кульки.
Сила Лоренца, що діє на заряджену частинку, дорівнює F = qv × B, де q — заряд, v — швидкість частинки, B — магнітна індукція. Значення векторного добутку — вектор, завжди перпендикулярний до обох початкових векторів, тому F ⊥ v. Скалярний добуток двох перпендикулярних векторів завжди дорівнює нулю, тому робота A = F ⋅ v = 0, а сила Лоренца не виконує роботи. Вона може змінити напрямок руху частинки, але ніколи не змінює швидкості.
Для рухомих тіл величина робота/час (потужність) інтегрується вздовж траєкторії точки прикладання сили. Таким чином, у будь-який момент швидкість виконання роботи силою (вимірюється в джоулях за секунду або ватах), є скалярним добутком вектора сили і вектора швидкості точки її прикладання. Цей скалярний добуток сили та швидкості називають миттєвою потужністю. Подібно до того, як швидкості можна інтегрувати за часом, щоб отримати загальний шлях, згідно з формулою Ньютона — Ляйбніца, загальна робота вздовж шляху так само є інтегралом за часом миттєвої потужності, прикладеної вздовж траєкторії точки прикладання сили.
Робота є результатом дії сили на точку, яка рухається вздовж кривої X зі швидкістю v в кожен момент. Малу роботу δA, яка виконується протягом часу dt, розраховують як де F ⋅ v — потужність протягом часу dt. Сума цих малих значень роботи за траєкторією точки дає роботу, де C — траєкторія від x(t1) до x(t2). Цей інтеграл обчислюється вздовж траєкторії частинки, і тому кажуть, що він залежить від форми траєкторії.
Якщо сила завжди спрямована вздовж цієї лінії, а величина сили F, то цей інтеграл спрощується до де s — переміщення. Якщо F постійна, крім того, що вона спрямована вздовж прямої, то інтеграл спрощується далі де s — переміщення точки.
Цей розрахунок можна узагальнити для постійної сили, яка не напрямлена вздовж прямої, якою рухається частинка. У цьому випадку скалярний добуток F ⋅ ds = F cos θ ds, де θ — кут між вектором сили та напрямком руху, тобто
Складова сили, перпендикулярна до переміщення тіла (наприклад, коли тіло рухається по коловій траєкторії під дією центральної сили), роботи не виконує, оскільки косинус 90° дорівнює нулю.[16] Таким чином, гравітаційна сила не виконує роботи під час руху планети коловою орбітою (це ідеальний випадок, оскільки практично всі орбіти злегка еліптичні). Крім того, над тілом, яке рухається по колу з постійною швидкістю і обмежене механічною силою, робота не виконується (приклад — рух із постійною швидкістю в ідеальній центрифузі без тертя).
Розрахунок роботи як «добутка сили й переміщення» застосовний лише в найпростіших обставинах, як зазначено вище. Якщо ж сила змінюється або якщо тіло рухається вздовж криволінійної траєкторії, наприклад, обертається, то для розрахунку виконаної роботи слід враховувати траєкторію точки прикладання сили, і лише складова сили, паралельна швидкості точки прикладання виконує роботу (додатна робота, коли напрямки збігаються, і від'ємна, коли протилежні). Цю складову сили можна описати скалярною величиною, яку називають скалярною тангенціальною складовою (F cos(θ), де θ — кут між силою та швидкістю). І тоді найзагальніше визначення роботи можна сформулювати так:

Таким чином, роботу змінної сили, можна виразити як визначений інтеграл сили за переміщенням.[21]
Якщо залежність переміщення від часу задано як ∆x(t), то робота змінної сили за час від t1 до t2 дорівнює:
- де — потужність.
Отже, роботу змінної сили можна виразити як визначений інтеграл потужності за часом.
Пара сил виникає внаслідок дії рівних протилежних сил на дві різні точки твердого тіла. Сума (рівнодійна) цих сил дорівнює нулю, але їх дія на тіло створює крутний момент M. Робота крутного моменту обчислюється як де M ⋅ ω — потужність протягом часу dt. Сума цих малих робіт за траєкторією руху твердого тіла дає роботу, Цей інтеграл обчислюється за траєкторією твердого тіла з кутовою швидкістю ω, яка змінюється з часом, тобто він залежить від форми траєкторії.
Якщо вектор кутової швидкості зберігає постійний напрямок, то він набуває вигляду де — кут повороту навколо постійного одиничного вектора S. У цьому випадку робота крутного моменту стає де C — траєкторія з до . Цей інтеграл залежить від форми траєкторії обертання .
Якщо крутний момент узгоджується з вектором кутової швидкості так, що і як крутний момент, так і кутова швидкість постійні, тоді робота набуває вигляду,[22]
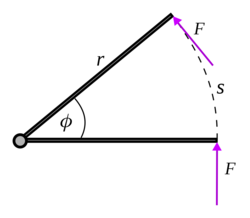
Цей результат легше зрозуміти, розглядаючи крутний момент як такий, що виникає від сили постійної величини F, прикладеної перпендикулярно до плеча важеля довжиною , як показано на малюнку. Ця сила діятиме на шляху, рівному довжині дуги кола , тому виконана робота Введемо крутний момент τ = Fr, щоб отримати як показано вище.
Зверніть увагу, що в роботу робить внесок лише складова крутного моменту в напрямку вектора кутової швидкості.
Скалярний добуток сили F і швидкості v точки її прикладання визначає миттєву потужність, яка надходить у систему. Інтеграл цієї потужності за траєкторією точки прикладання, C = x(t), визначає роботу, яку вносить у систему сила.
Отже, робота, яку виконує сила F над тілом, яке рухається вздовж кривої C визначається криволінійним інтегралом: де dx(t) визначає траєкторію C, а v — швидкість уздовж цієї траєкторії. Цей інтеграл враховує траєкторію, уздовж якої рухається тіло, тобто, робота залежить від форми траєкторії.
Похідна за часом від інтеграла для роботи дає миттєву потужність,
Якщо робота прикладеної сили не залежить від шляху, то робота, виконана силою, відповідно до градієнтної теореми, визначає потенціальну функцію, яка обчислюється на початку та в кінці траєкторії точки прикладання. Це означає, що існує потенціальна функція U(x), яку можна обчислити в двох точках x(t1) і x(t2) щоб отримати роботу за будь-якою траєкторією між цими двома точками. Традиційно цю функцію визначати зі знаком «мінус», так що додатна робота означає зменшення потенціалу, тобто
Функцію U(x) називають потенціальною енергією, пов'язаною з прикладеною силою. Силу, пов'язану з такою потенціальною функцією, називають консервативною. Прикладами сил, які мають потенціальну енергію, є сила тяжіння та сила пружності.
У цьому випадку градієнт роботи має вигляд і кажуть, що сила F є «похідною потенціалу».[23]
Оскільки потенціал U визначає силу F у кожній точці x простору, сукупність сил називають силовим полем. Потужність, прикладена до тіла з боку силового поля, визначається градієнтом роботи або потенціалу в напрямку швидкості v тіла, тобто
За відсутності інших сил сила тяжіння спричиняє постійне прискорення вниз кожного вільно рухомого тіла. Біля поверхні Землі прискорення сили тяжіння становить g = 9.8 м⋅с−2, а сила тяжіння на тіло масою m дорівнює Fg = mg . Зручно уявляти, що сила тяжіння прикладена в центрі мас об'єкта.
Якщо тіло вагою mg зміщується вгору або вниз на вертикальну відстань y2 − y1, робота A, виконана над тілом, дорівнює: де — вага (в ньютонах у SI), а — зміна висоти . Зауважте, що робота сили тяжіння залежить лише від вертикального руху тіла. Наявність тертя не впливає на роботу, яку виконує над тілом сила тяжіння.
Сила тяжіння, з якою маса M діє на іншу масу m визначається як де r — радіус-вектор від M до m, а r̂ — одиничний вектор у напрямі r.
Нехай тіло масою m рухається зі швидкістю v; тоді робота сили тяжіння над цією масою під час її переміщення з положення r(t1) до r(t2) визначається як Зауважте, що положення та швидкість маси m визначаються як де er і et — радіальний і тангенціальний одиничні вектори, напрямлені відносно вектора[прояснити] від M до m; крім того Використаємо це, щоб спростити формулу для роботи сили тяжіння: Цей розрахунок використовує той факт, що Функція гравітаційна потенціальна функція, також відома як гравітаційна потенціальна енергія. Знак «мінус» відповідає домовленості про те, що робота виконується за рахунок втрати потенціальної енергії.

Розглянемо пружину, в якій виникає горизонтальна сила F = (−kx, 0, 0), пропорційна її видовженню в напрямку незалежно від того, як рухається тіло. Роботу цієї пружини над тілом, що рухається в просторі вздовж кривої X(t) = (x(t), y(t), z(t)), розраховують за її швидкістю v = (vx, vy, vz): Для зручності вважайте, що контакт із пружиною відбувається в момент часу t = 0, тоді інтеграл від добутку відстані x і проєкції швидкості на вісь x, xvxdt, за часом t дорівнює 1/2x2. Робота дорівнює добутку відстані на силу пружності, яка також залежить від відстані; отже маємо x2.
Робота дії газу на його оточення: де p — тиск, V — об'єм, a і b — початковий і кінцевий об'єми.
Принцип роботи та кінетичної енергії (також відомий як принцип роботи–енергії) стверджує, що робота, виконана всіма силами, які діють на частинку (робота рівнодійної сил), дорівнює зміні кінетичної енергії частинки.[24] Тобто робота А, яку виконує рівнодійна сил на частинку, дорівнює зміні кінетичної енергії частинки ,[22] де і — швидкості частинки до і після виконання роботи, m — її маса.
Виведення принципу роботи-енергії починається з другого закону руху Ньютона та рівнодійної сил, що діють на частинку. Обчислення скалярного добутку сили на швидкість частинки оцінює миттєву потужність, надану системі.[25] (Обмеження визначають напрямок руху частинки, гарантуючи відсутність компонента швидкості в напрямку реакцій в'язей. Це також означає, що реакції не додають миттєвої потужності.) Інтеграл за часом цього скалярного рівняння дає роботу, а кінетичну енергію за скалярним добутком прискорення та швидкості[прояснити]. Той факт, що принцип роботи-енергії усуває реакції, лежить в основі механіки Лагранжа.[26]
У цьому розділі зосереджено увагу на принципі роботи–енергії стосовно динаміки частинок. У загальніших системах робота може змінювати потенціальну енергію механічного пристрою, теплову енергію в тепловій системі або електричну енергію в електричному пристрої. Робота переносить енергію з одного місця в інше або переводить її з однієї форми в іншу.
У випадку, коли рівнодійна F постійна як за величиною, так і за напрямом і паралельна швидкості частинки, частинка рухається з постійним прискоренням вздовж прямої лінії.[27] Співвідношення між рівнодійною та прискоренням визначається рівнянням F = ma (другий закон Ньютона), а переміщення частинки s можна виразити рівнянням що випливає з (див. Рівняння руху).
Робота рівнодійної сил обчислюється як добуток її величини на зміщення частинки. Підставляючи наведені вище рівняння, отримуємо:
Інше виведення:
У загальному випадку прямолінійного руху, коли рівнодійна F не постійна за величиною, але постійна за напрямом і паралельна швидкості частинки, роботу слід інтегрувати за траєкторією частинки:
Для будь-якої рівнодійної, що діє на частинку, яка рухається вздовж будь-якої криволінійної траєкторії, за допомогою простого виведення, аналогічного наведеному вище рівнянню, можна продемонструвати, що робота дорівнює зміні кінетичної енергії частинки. У цьому полягає принцип роботи-енергії :
Рівність випливає з рівності і визначення :
У динаміці частинок формулу рівності роботи, виконуваної над системою, зміні її кінетичної енергії отримуємо інтегруванням другого закону руху Ньютона. Зауважимо, що рівнодійну, використовувану в законах Ньютона, можна розкласти на сили, прикладені до частинки, і реакції в'язей, які обмежують рух частини. Важливо, що робота реакцій є нульовою, тому принцип роботи-енергії враховує лише роботу прикладених сил.
Щоб побачити це, розглянемо частинку P, яка рухається траєкторією X(t) під дією сили F. Ізолюймо частинку від її оточення, щоб виявити силу реакції R, тоді другий закон Ньютона набуде вигляду де m — маса частинки.
Зверніть увагу, що n крапок над вектором означає його n-ну похідну за часом. Скалярний добуток кожної з частин рівняння другого закону Ньютона на вектор швидкості дає оскільки реакції перпендикулярні до швидкості частинки. Проінтегруймо це рівняння вздовж траєкторії від точки X(t1) до точки X(t2):
Ліва частина цього рівняння є роботою сили, яка діє на частинку вздовж траєкторії від моменту часу t1 до моменту часу t2. Це також можна записати як Цей інтеграл обчислюється вздовж траєкторії X(t) частинки, отже, залежить від форми траєкторії.
Праву частину інтеграла можна спростити за допомогою такої тотожності (див. правило добутку). Тепер воно інтегрується явно і дає зміну кінетичної енергії, де кінетична енергія частинки визначається скалярною величиною,
Корисно розділити вектори швидкості та прискорення на тангенціальну та нормальну складові вздовж траєкторії X(t), так що де Тоді скалярний добуток швидкості на прискорення у другому законі Ньютона набуває вигляду де кінетична енергія частинки визначається скалярною величиною,
Результатом є принцип роботи-енергії для динаміки частинок, Цей висновок можна узагальнити на довільні системи твердих тіл.
Розглянемо випадок, коли транспортний засіб рухається по прямій горизонтальній траєкторії під дією рушійної сили та сили тяжіння, які в сумі дорівнюють F. Сила реакції між транспортним засобом і дорогою R, отже, Для зручності спрямуємо вісь X уздовж траєкторії, тоді X = (d, 0), а швидкість V = (v, 0), звідки R ⋅ V = 0 і F ⋅ V = Fxv, де — проєкція F на вісь X, отже Інтегрування обох частин дає Якщо Fx постійна вздовж траєкторії, то інтеграл швидкості дає переміщення, отже
Як приклад розглянемо автомобіль, який гальмує до зупинки, де k — коефіцієнт тертя, а P — вага автомобіля. Тоді проєкція сили на траєкторію Fx = −kP. Швидкість автомобіля можна визначити за гальмівним шляхом s за принципом роботи-енергії, У цій формулі використано той факт, що маса транспортного засобу дорівнює m = P/g.


Розглянемо транспортний засіб, який рушає з місця та рухається вниз по похилій площині (наприклад, гірській дорозі). Принцип роботи-енергії дає змогу обчислити найменшу відстань, яку має пройти транспортний засіб, щоб досягти швидкості V, скажімо, 54 км/год (15 м/с). Тертя кочення та опір повітря сповільнять транспортний засіб, тому фактична відстань буде більшою, ніж якщо цими силами знехтувати.
Нехай траєкторія транспортного засобу, що рухається дорогою, буде крива в тривимірному просторі X(t). Рухатися транспортний засіб змушує постійна сила тяжіння F = (0, 0, W), тоді як обмежує рух реакція дороги R. Другий закон Ньютона дає, Скалярний добуток цього рівняння на швидкість V = (vx, vy, vz) дає де V — величина V. Сила реакції з боку дороги зникає з цього рівняння, оскільки R ⋅ V = 0, що означає, що вона не виконує роботи. Проінтегрувавши обидві частини, маємо Вага P постійна вздовж траєкторії, а інтеграл вертикальної швидкості дає вертикальне зміщення, тому Нагадаємо, що . Зауважте, що цей результат не залежить від форми дороги, якою рухається транспортний засіб.
Щоб визначити відстань уздовж дороги, припустимо, що похил становить 6 %, що є доволі крутим схилом. Це означає, що висота зменшується на 6 метрі на кожні 100 пройдених метрів — для таких малих кутів значення синуса і тангенса приблизно рівні. Отже, відстань s у метрах униз уздовж схилу 6 % для досягнення швидкості V становить принаймні У розрахунку використано той факт, що вага транспортного засобу становить P = mg.
Роботу сил, що діють у різних точках на одне тверде тіло, можна обчислити за роботою рівнодійних сили та крутного моменту[en].
Нехай сили F1, F2, … , Fn діють на точки твердого тіла X1, X2, …, Xn.
Траєкторії Xi, i = 1, … , n визначаються рухом твердого тіла. Цей рух задано набором обертань [A(t)] і траєкторією d(t) опорної точки в тілі. Нехай координати xi, i = 1, … , n визначають ці точки в системі відліку M рухомого твердого тіла, так що траєкторії, спостережувані в нерухомій системі F, задані як
Швидкості точок Xi вздовж їхніх траєкторій становлять де ω — вектор кутової швидкості, отриманий з кососиметричної матриці відомої як матриця кутової швидкості.
Роботу сил на малому переміщенні δri можна визначити апроксимації переміщення δr = vδt, отже або
Після перетворень маємо де F і М — рівнодійні сила та крутний момент, що діють у точці відліку d рухомої сиситеми відліку М у твердому тілі[прояснити].
- ↑ а б Krebs, Robert E. (2004). Groundbreaking Experiments, Inventions, and Discoveries of the Middle Ages. Greenwood Publishing Group. с. 163. ISBN 978-0-313-32433-8. Процитовано 21 травня 2008.
- ↑ Stephen, Donald; Lowell Cardwell (2001). Wheels, clocks, and rockets: a history of technology. US: W.W. Norton & Company. с. 85—87. ISBN 978-0-393-32175-3.
- ↑ Mendelson, Kenneth S. (13 лютого 2003). Physical and colloquial meanings of the term "work". American Journal of Physics (англ.). 71 (3): 279—281. Bibcode:2003AmJPh..71..279M. doi:10.1119/1.1522707. ISSN 0002-9505.
- ↑ Descartes, R. (2013). Bennett, J. (ред.). Selected correspondence of Descartes (PDF). с. 50.
- ↑ Iltis, C. (1971). Leibniz and the vis viva controversy (PDF). Isis. 62 (1): 21–35 (specifically p. 24). doi:10.1086/350705.
- ↑ Smeaton, John (1759). Experimental Enquiry Concerning the Natural Powers of Water and Wind to Turn Mills and Other Machines Depending on a Circular Motion. Philosophical Transactions of the Royal Society. 51: 105. doi:10.1098/rstl.1759.0019.
- ↑ Coriolis, Gustave (1829). Calculation of the Effect of Machines, or Considerations on the Use of Engines and their Evaluation. Carilian-Goeury, Libraire (Paris).
- ↑ Poncelet, Jean-Victor (1839). Introduction a la mécanique industrielle, physique ou expérimentale.
- ↑ Grattan-Guinness, Ivor (1984). Work for the workers: Advances in engineering mechanics and instruction in France, 1800–1830. Annals of Science. 41 (1): 1—33. doi:10.1080/00033798400200101. Процитовано 21 грудня 2024.
- ↑ Dugas, R. (1955). A History of Mechanics. Switzerland: Éditions du Griffon. с. 128.
- ↑ Poncelet, Jean Victor (1826). Cours de mécanique appliquée aux machines.
- ↑ Coriolis, Gustave (1829). Calculation of the Effect of Machines, or Considerations on the Use of Engines and their Evaluation. Carilian-Goeury, Libraire (Paris).
- ↑ Units with special names and symbols; units that incorporate special names and symbols. The International System of Units (SI) (вид. 8th). International Bureau of Weights and Measures. 2006. Архів оригіналу за 20 квітня 2013. Процитовано 27 жовтня 2012.
- ↑ Elements of Physics: For Students of Science and Engineering. ISBN 978-0-13-268375-3.
- ↑ а б McGrath, Kimberley A., ред. (5 травня 2010). World of physics (English) (вид. 1st). Detroit: Gale. Work and potential energy. ISBN 978-0-7876-3651-7.
- ↑ а б Walker, Jearl; Halliday, David; Resnick, Robert (2011). Fundamentals of physics (вид. 9th). Hoboken, NJ: Wiley. с. 154. ISBN 9780470469118.
- ↑ Goldstein, Herbert (2002). Classical mechanics (вид. 3rd). Addison Wesley. ISBN 978-0-201-65702-9. OCLC 47056311.
- ↑ Rogalski, Mircea S. (2018). Advanced University Physics (вид. 2nd). Boca Raton: Chapman and Hall/CRC. ISBN 9781351991988.
- ↑ а б The Feynman Lectures on Physics Vol. I Ch. 14: Work and Potential Energy (conclusion). feynmanlectures.caltech.edu.
- ↑ Greenwood, Donald T. (1997). Classical dynamics. Mineola, N.Y.: Dover Publications. ISBN 9780486138794.
- ↑ MindTap - Cengage Learning. ng.cengage.com. Процитовано 16 жовтня 2023.
- ↑ а б Hugh D. Young & Roger A. Freedman (2008). University Physics (вид. 12th). Addison-Wesley. с. 329. ISBN 978-0-321-50130-1.
- ↑ Taylor, John R. (2005). Classical Mechanics (англ.). University Science Books. ISBN 978-1-891389-22-1.
- ↑ Andrew Pytel; Jaan Kiusalaas (2010). Engineering Mechanics: Dynamics – SI Version, Volume 2 (вид. 3rd). Cengage Learning. с. 654. ISBN 9780495295631.
- ↑ Paul, Burton (1979). Kinematics and Dynamics of Planar Machinery (англ.). Prentice-Hall. ISBN 978-0-13-516062-6.
- ↑ Whittaker, E. T. (1904). A treatise on the analytical dynamics of particles and rigid bodies (англ.). Cambridge University Press.
- ↑ Work–energy principle. www.wwu.edu. Архів оригіналу за 30 травня 2012. Процитовано 6 серпня 2012.
- Єжов С. М., Макарець М. В., Романенко О. В. Класична механіка. — К. : ВПЦ "Київський університет", 2008. — 480 с.
- Федорченко А. М. Теоретична механіка. — К. : Вища школа, 1975. — 516 с.
- Зв'язок між роботою і енергією у випадку системи частинок
- Робота // Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.






























































































![{\displaystyle \mathbf {X} _{i}(t)=[A(t)]\mathbf {x} _{i}+\mathbf {d} (t)\quad i=1,\ldots ,n.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/007f113cb9f2c64f292276ef03331e590deddaca)

![{\displaystyle [\Omega ]={\dot {A}}A^{\mathsf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f944ca8607581db78ecdfff09726268f85986c90)


