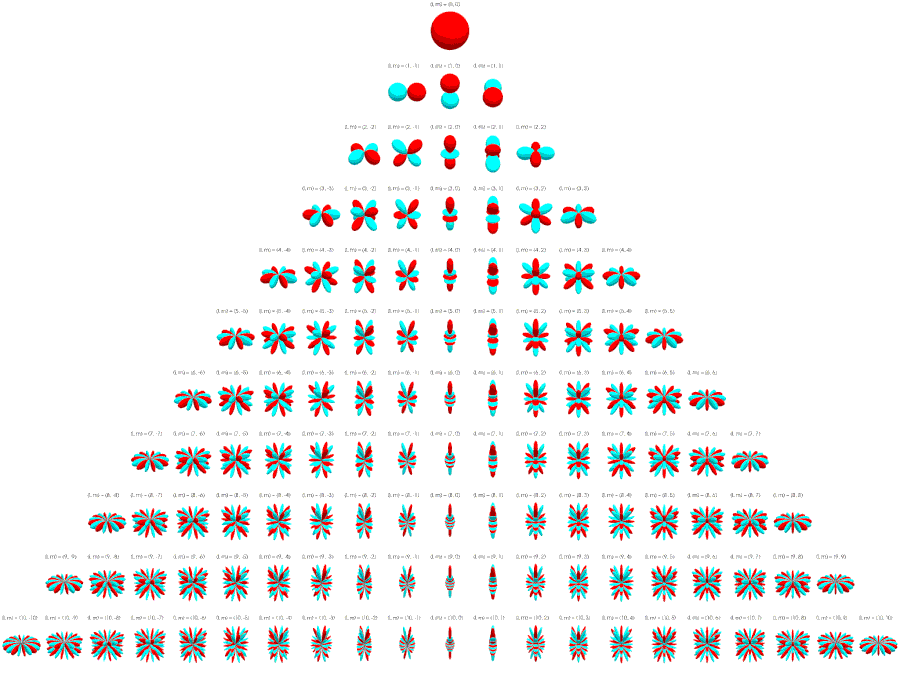
Візуальне представлення перших декількох дійсних сферичних гармонік. Голубий колір відповідає області, де функції додатні, а жовтий -- де від'ємні. Відстань від початку координат відповідає абсолютній величні гармоніки
Y
ℓ
m
(
θ
,
φ
)
{\displaystyle Y_{\ell }^{m}(\theta ,\varphi )}
(
θ
,
φ
)
{\displaystyle (\theta ,\varphi )}
Дана стаття містить перелік ортонормованих сферичних гармонік
ℓ
=
10
{\displaystyle \ell =10}
сферичній системі координат
r
,
φ
,
θ
{\displaystyle r,\varphi ,\theta }
декартових координатах
x
,
y
,
z
{\displaystyle x,y,z}
, та
r
{\displaystyle r}
r
=
x
2
+
y
2
+
z
2
{\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
{
cos
(
θ
)
=
z
/
r
e
±
i
φ
⋅
sin
(
θ
)
=
(
x
±
i
y
)
/
r
{\displaystyle {\begin{cases}\cos(\theta )&=z/r\\e^{\pm i\varphi }\cdot \sin(\theta )&=(x\pm iy)/r\end{cases}}}
власні коливання тривимірного сферичного об'єму (кулі ).
Для
l
=
0
,
1
,
…
,
5
{\displaystyle l=0,1,\ldots ,5}
[ 1]
Y
0
0
(
θ
,
φ
)
=
1
2
1
π
{\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}
Y
1
−
1
(
θ
,
φ
)
=
1
2
3
2
π
⋅
e
−
i
φ
⋅
sin
θ
=
1
2
3
2
π
⋅
(
x
−
i
y
)
r
Y
1
0
(
θ
,
φ
)
=
1
2
3
π
⋅
cos
θ
=
1
2
3
π
⋅
z
r
Y
1
1
(
θ
,
φ
)
=
−
1
2
3
2
π
⋅
e
i
φ
⋅
sin
θ
=
−
1
2
3
2
π
⋅
(
x
+
i
y
)
r
{\displaystyle {\begin{aligned}Y_{1}^{-1}(\theta ,\varphi )&=&&{1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta &&=&&{1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x-iy) \over r}\\Y_{1}^{0}(\theta ,\varphi )&=&&{1 \over 2}{\sqrt {3 \over \pi }}\cdot \cos \theta &&=&&{1 \over 2}{\sqrt {3 \over \pi }}\cdot {z \over r}\\Y_{1}^{1}(\theta ,\varphi )&=&-&{1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta &&=&-&{1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x+iy) \over r}\end{aligned}}}
Y
2
−
2
(
θ
,
φ
)
=
1
4
15
2
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
=
1
4
15
2
π
⋅
(
x
−
i
y
)
2
r
2
Y
2
−
1
(
θ
,
φ
)
=
1
2
15
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
cos
θ
=
1
2
15
2
π
⋅
(
x
−
i
y
)
⋅
z
r
2
Y
2
0
(
θ
,
φ
)
=
1
4
5
π
⋅
(
3
cos
2
θ
−
1
)
=
1
4
5
π
⋅
(
3
z
2
−
r
2
)
r
2
Y
2
1
(
θ
,
φ
)
=
−
1
2
15
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
cos
θ
=
−
1
2
15
2
π
⋅
(
x
+
i
y
)
⋅
z
r
2
Y
2
2
(
θ
,
φ
)
=
1
4
15
2
π
⋅
e
2
i
φ
⋅
sin
2
θ
=
1
4
15
2
π
⋅
(
x
+
i
y
)
2
r
2
{\displaystyle {\begin{aligned}Y_{2}^{-2}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \quad &&=&&{1 \over 4}{\sqrt {15 \over 2\pi }}\cdot {(x-iy)^{2} \over r^{2}}&\\Y_{2}^{-1}(\theta ,\varphi )&=&&{1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot \cos \theta \quad &&=&&{1 \over 2}{\sqrt {15 \over 2\pi }}\cdot {(x-iy)\cdot z \over r^{2}}&\\Y_{2}^{0}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {5 \over \pi }}\cdot (3\cos ^{2}\theta -1)\quad &&=&&{1 \over 4}{\sqrt {5 \over \pi }}\cdot {(3z^{2}-r^{2}) \over r^{2}}&\\Y_{2}^{1}(\theta ,\varphi )&=&-&{1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot \cos \theta \quad &&=&-&{1 \over 2}{\sqrt {15 \over 2\pi }}\cdot {(x+iy)\cdot z \over r^{2}}&\\Y_{2}^{2}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \quad &&=&&{1 \over 4}{\sqrt {15 \over 2\pi }}\cdot {(x+iy)^{2} \over r^{2}}&\\{}\end{aligned}}}
Y
3
−
3
(
θ
,
φ
)
=
1
8
35
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
=
1
8
35
π
⋅
(
x
−
i
y
)
3
r
3
Y
3
−
2
(
θ
,
φ
)
=
1
4
105
2
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
cos
θ
=
1
4
105
2
π
⋅
(
x
−
i
y
)
2
⋅
z
r
3
Y
3
−
1
(
θ
,
φ
)
=
1
8
21
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
5
cos
2
θ
−
1
)
=
1
8
21
π
⋅
(
x
−
i
y
)
⋅
(
5
z
2
−
r
2
)
r
3
Y
3
0
(
θ
,
φ
)
=
1
4
7
π
⋅
(
5
cos
3
θ
−
3
cos
θ
)
=
1
4
7
π
⋅
(
5
z
3
−
3
z
r
2
)
r
3
Y
3
1
(
θ
,
φ
)
=
−
1
8
21
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
5
cos
2
θ
−
1
)
=
−
1
8
21
π
⋅
(
x
+
i
y
)
⋅
(
5
z
2
−
r
2
)
r
3
Y
3
2
(
θ
,
φ
)
=
1
4
105
2
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
cos
θ
=
1
4
105
2
π
⋅
(
x
+
i
y
)
2
⋅
z
r
3
Y
3
3
(
θ
,
φ
)
=
−
1
8
35
π
⋅
e
3
i
φ
⋅
sin
3
θ
=
−
1
8
35
π
⋅
(
x
+
i
y
)
3
r
3
{\displaystyle {\begin{aligned}Y_{3}^{-3}(\theta ,\varphi )&=&&{1 \over 8}{\sqrt {35 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \quad &&=&&{1 \over 8}{\sqrt {35 \over \pi }}\cdot {(x-iy)^{3} \over r^{3}}&\\Y_{3}^{-2}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {105 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot \cos \theta \quad &&=&&{1 \over 4}{\sqrt {105 \over 2\pi }}\cdot {(x-iy)^{2}\cdot z \over r^{3}}&\\Y_{3}^{-1}(\theta ,\varphi )&=&&{1 \over 8}{\sqrt {21 \over \pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (5\cos ^{2}\theta -1)\quad &&=&&{1 \over 8}{\sqrt {21 \over \pi }}\cdot {(x-iy)\cdot (5z^{2}-r^{2}) \over r^{3}}&\\Y_{3}^{0}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {7 \over \pi }}\cdot (5\cos ^{3}\theta -3\cos \theta )\quad &&=&&{1 \over 4}{\sqrt {7 \over \pi }}\cdot {(5z^{3}-3zr^{2}) \over r^{3}}&\\Y_{3}^{1}(\theta ,\varphi )&=&-&{1 \over 8}{\sqrt {21 \over \pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (5\cos ^{2}\theta -1)\quad &&=&&{-1 \over 8}{\sqrt {21 \over \pi }}\cdot {(x+iy)\cdot (5z^{2}-r^{2}) \over r^{3}}&\\Y_{3}^{2}(\theta ,\varphi )&=&&{1 \over 4}{\sqrt {105 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot \cos \theta \quad &&=&&{1 \over 4}{\sqrt {105 \over 2\pi }}\cdot {(x+iy)^{2}\cdot z \over r^{3}}&\\Y_{3}^{3}(\theta ,\varphi )&=&-&{1 \over 8}{\sqrt {35 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \quad &&=&&{-1 \over 8}{\sqrt {35 \over \pi }}\cdot {(x+iy)^{3} \over r^{3}}&\end{aligned}}}
Y
4
−
4
(
θ
,
φ
)
=
3
16
35
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
=
3
16
35
2
π
⋅
(
x
−
i
y
)
4
r
4
Y
4
−
3
(
θ
,
φ
)
=
3
8
35
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
cos
θ
=
3
8
35
π
⋅
(
x
−
i
y
)
3
z
r
4
Y
4
−
2
(
θ
,
φ
)
=
3
8
5
2
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
7
cos
2
θ
−
1
)
=
3
8
5
2
π
⋅
(
x
−
i
y
)
2
⋅
(
7
z
2
−
r
2
)
r
4
Y
4
−
1
(
θ
,
φ
)
=
3
8
5
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
7
cos
3
θ
−
3
cos
θ
)
=
3
8
5
π
⋅
(
x
−
i
y
)
⋅
(
7
z
3
−
3
z
r
2
)
r
4
Y
4
0
(
θ
,
φ
)
=
3
16
1
π
⋅
(
35
cos
4
θ
−
30
cos
2
θ
+
3
)
=
3
16
1
π
⋅
(
35
z
4
−
30
z
2
r
2
+
3
r
4
)
r
4
Y
4
1
(
θ
,
φ
)
=
−
3
8
5
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
7
cos
3
θ
−
3
cos
θ
)
=
−
3
8
5
π
⋅
(
x
+
i
y
)
⋅
(
7
z
3
−
3
z
r
2
)
r
4
Y
4
2
(
θ
,
φ
)
=
3
8
5
2
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
7
cos
2
θ
−
1
)
=
3
8
5
2
π
⋅
(
x
+
i
y
)
2
⋅
(
7
z
2
−
r
2
)
r
4
Y
4
3
(
θ
,
φ
)
=
−
3
8
35
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
cos
θ
=
−
3
8
35
π
⋅
(
x
+
i
y
)
3
z
r
4
Y
4
4
(
θ
,
φ
)
=
3
16
35
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
=
3
16
35
2
π
⋅
(
x
+
i
y
)
4
r
4
{\displaystyle {\begin{aligned}Y_{4}^{-4}(\theta ,\varphi )&={3 \over 16}{\sqrt {35 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta ={\frac {3}{16}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {(x-iy)^{4}}{r^{4}}}\\Y_{4}^{-3}(\theta ,\varphi )&={3 \over 8}{\sqrt {35 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot \cos \theta ={\frac {3}{8}}{\sqrt {\frac {35}{\pi }}}\cdot {\frac {(x-iy)^{3}z}{r^{4}}}\\Y_{4}^{-2}(\theta ,\varphi )&={3 \over 8}{\sqrt {5 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (7\cos ^{2}\theta -1)={\frac {3}{8}}{\sqrt {\frac {5}{2\pi }}}\cdot {\frac {(x-iy)^{2}\cdot (7z^{2}-r^{2})}{r^{4}}}\\Y_{4}^{-1}(\theta ,\varphi )&={3 \over 8}{\sqrt {5 \over \pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (7\cos ^{3}\theta -3\cos \theta )={\frac {3}{8}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {(x-iy)\cdot (7z^{3}-3zr^{2})}{r^{4}}}\\Y_{4}^{0}(\theta ,\varphi )&={3 \over 16}{\sqrt {1 \over \pi }}\cdot (35\cos ^{4}\theta -30\cos ^{2}\theta +3)={\frac {3}{16}}{\sqrt {\frac {1}{\pi }}}\cdot {\frac {(35z^{4}-30z^{2}r^{2}+3r^{4})}{r^{4}}}\\Y_{4}^{1}(\theta ,\varphi )&={-3 \over 8}{\sqrt {5 \over \pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (7\cos ^{3}\theta -3\cos \theta )={\frac {-3}{8}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {(x+iy)\cdot (7z^{3}-3zr^{2})}{r^{4}}}\\Y_{4}^{2}(\theta ,\varphi )&={3 \over 8}{\sqrt {5 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (7\cos ^{2}\theta -1)={\frac {3}{8}}{\sqrt {\frac {5}{2\pi }}}\cdot {\frac {(x+iy)^{2}\cdot (7z^{2}-r^{2})}{r^{4}}}\\Y_{4}^{3}(\theta ,\varphi )&={-3 \over 8}{\sqrt {35 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot \cos \theta ={\frac {-3}{8}}{\sqrt {\frac {35}{\pi }}}\cdot {\frac {(x+iy)^{3}z}{r^{4}}}\\Y_{4}^{4}(\theta ,\varphi )&={3 \over 16}{\sqrt {35 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta ={\frac {3}{16}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {(x+iy)^{4}}{r^{4}}}\end{aligned}}}
Y
5
−
5
(
θ
,
φ
)
=
3
32
77
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
Y
5
−
4
(
θ
,
φ
)
=
3
16
385
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
cos
θ
Y
5
−
3
(
θ
,
φ
)
=
1
32
385
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
9
cos
2
θ
−
1
)
Y
5
−
2
(
θ
,
φ
)
=
1
8
1155
2
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
3
cos
3
θ
−
cos
θ
)
Y
5
−
1
(
θ
,
φ
)
=
1
16
165
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
21
cos
4
θ
−
14
cos
2
θ
+
1
)
Y
5
0
(
θ
,
φ
)
=
1
16
11
π
⋅
(
63
cos
5
θ
−
70
cos
3
θ
+
15
cos
θ
)
Y
5
1
(
θ
,
φ
)
=
−
1
16
165
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
21
cos
4
θ
−
14
cos
2
θ
+
1
)
Y
5
2
(
θ
,
φ
)
=
1
8
1155
2
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
3
cos
3
θ
−
cos
θ
)
Y
5
3
(
θ
,
φ
)
=
−
1
32
385
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
9
cos
2
θ
−
1
)
Y
5
4
(
θ
,
φ
)
=
3
16
385
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
cos
θ
Y
5
5
(
θ
,
φ
)
=
−
3
32
77
π
⋅
e
5
i
φ
⋅
sin
5
θ
{\displaystyle {\begin{aligned}Y_{5}^{-5}(\theta ,\varphi )&={3 \over 32}{\sqrt {77 \over \pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \\Y_{5}^{-4}(\theta ,\varphi )&={3 \over 16}{\sqrt {385 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot \cos \theta \\Y_{5}^{-3}(\theta ,\varphi )&={1 \over 32}{\sqrt {385 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (9\cos ^{2}\theta -1)\\Y_{5}^{-2}(\theta ,\varphi )&={1 \over 8}{\sqrt {1155 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (3\cos ^{3}\theta -\cos \theta )\\Y_{5}^{-1}(\theta ,\varphi )&={1 \over 16}{\sqrt {165 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (21\cos ^{4}\theta -14\cos ^{2}\theta +1)\\Y_{5}^{0}(\theta ,\varphi )&={1 \over 16}{\sqrt {11 \over \pi }}\cdot (63\cos ^{5}\theta -70\cos ^{3}\theta +15\cos \theta )\\Y_{5}^{1}(\theta ,\varphi )&={-1 \over 16}{\sqrt {165 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (21\cos ^{4}\theta -14\cos ^{2}\theta +1)\\Y_{5}^{2}(\theta ,\varphi )&={1 \over 8}{\sqrt {1155 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (3\cos ^{3}\theta -\cos \theta )\\Y_{5}^{3}(\theta ,\varphi )&={-1 \over 32}{\sqrt {385 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (9\cos ^{2}\theta -1)\\Y_{5}^{4}(\theta ,\varphi )&={3 \over 16}{\sqrt {385 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot \cos \theta \\Y_{5}^{5}(\theta ,\varphi )&={-3 \over 32}{\sqrt {77 \over \pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \end{aligned}}}
Y
6
−
6
(
θ
,
φ
)
=
1
64
3003
π
⋅
e
−
6
i
φ
⋅
sin
6
θ
Y
6
−
5
(
θ
,
φ
)
=
3
32
1001
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
⋅
cos
θ
Y
6
−
4
(
θ
,
φ
)
=
3
32
91
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
(
11
cos
2
θ
−
1
)
Y
6
−
3
(
θ
,
φ
)
=
1
32
1365
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
11
cos
3
θ
−
3
cos
θ
)
Y
6
−
2
(
θ
,
φ
)
=
1
64
1365
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
33
cos
4
θ
−
18
cos
2
θ
+
1
)
Y
6
−
1
(
θ
,
φ
)
=
1
16
273
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
33
cos
5
θ
−
30
cos
3
θ
+
5
cos
θ
)
Y
6
0
(
θ
,
φ
)
=
1
32
13
π
⋅
(
231
cos
6
θ
−
315
cos
4
θ
+
105
cos
2
θ
−
5
)
Y
6
1
(
θ
,
φ
)
=
−
1
16
273
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
33
cos
5
θ
−
30
cos
3
θ
+
5
cos
θ
)
Y
6
2
(
θ
,
φ
)
=
1
64
1365
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
33
cos
4
θ
−
18
cos
2
θ
+
1
)
Y
6
3
(
θ
,
φ
)
=
−
1
32
1365
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
11
cos
3
θ
−
3
cos
θ
)
Y
6
4
(
θ
,
φ
)
=
3
32
91
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
(
11
cos
2
θ
−
1
)
Y
6
5
(
θ
,
φ
)
=
−
3
32
1001
π
⋅
e
5
i
φ
⋅
sin
5
θ
⋅
cos
θ
Y
6
6
(
θ
,
φ
)
=
1
64
3003
π
⋅
e
6
i
φ
⋅
sin
6
θ
{\displaystyle {\begin{aligned}Y_{6}^{-6}(\theta ,\varphi )&={1 \over 64}{\sqrt {3003 \over \pi }}\cdot e^{-6i\varphi }\cdot \sin ^{6}\theta \\Y_{6}^{-5}(\theta ,\varphi )&={3 \over 32}{\sqrt {1001 \over \pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \cdot \cos \theta \\Y_{6}^{-4}(\theta ,\varphi )&={3 \over 32}{\sqrt {91 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot (11\cos ^{2}\theta -1)\\Y_{6}^{-3}(\theta ,\varphi )&={1 \over 32}{\sqrt {1365 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (11\cos ^{3}\theta -3\cos \theta )\\Y_{6}^{-2}(\theta ,\varphi )&={1 \over 64}{\sqrt {1365 \over \pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (33\cos ^{4}\theta -18\cos ^{2}\theta +1)\\Y_{6}^{-1}(\theta ,\varphi )&={1 \over 16}{\sqrt {273 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (33\cos ^{5}\theta -30\cos ^{3}\theta +5\cos \theta )\\Y_{6}^{0}(\theta ,\varphi )&={1 \over 32}{\sqrt {13 \over \pi }}\cdot (231\cos ^{6}\theta -315\cos ^{4}\theta +105\cos ^{2}\theta -5)\\Y_{6}^{1}(\theta ,\varphi )&=-{1 \over 16}{\sqrt {273 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (33\cos ^{5}\theta -30\cos ^{3}\theta +5\cos \theta )\\Y_{6}^{2}(\theta ,\varphi )&={1 \over 64}{\sqrt {1365 \over \pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (33\cos ^{4}\theta -18\cos ^{2}\theta +1)\\Y_{6}^{3}(\theta ,\varphi )&=-{1 \over 32}{\sqrt {1365 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (11\cos ^{3}\theta -3\cos \theta )\\Y_{6}^{4}(\theta ,\varphi )&={3 \over 32}{\sqrt {91 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot (11\cos ^{2}\theta -1)\\Y_{6}^{5}(\theta ,\varphi )&=-{3 \over 32}{\sqrt {1001 \over \pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \cdot \cos \theta \\Y_{6}^{6}(\theta ,\varphi )&={1 \over 64}{\sqrt {3003 \over \pi }}\cdot e^{6i\varphi }\cdot \sin ^{6}\theta \end{aligned}}}
Y
7
−
7
(
θ
,
φ
)
=
3
64
715
2
π
⋅
e
−
7
i
φ
⋅
sin
7
θ
Y
7
−
6
(
θ
,
φ
)
=
3
64
5005
π
⋅
e
−
6
i
φ
⋅
sin
6
θ
⋅
cos
θ
Y
7
−
5
(
θ
,
φ
)
=
3
64
385
2
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
⋅
(
13
cos
2
θ
−
1
)
Y
7
−
4
(
θ
,
φ
)
=
3
32
385
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
(
13
cos
3
θ
−
3
cos
θ
)
Y
7
−
3
(
θ
,
φ
)
=
3
64
35
2
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
143
cos
4
θ
−
66
cos
2
θ
+
3
)
Y
7
−
2
(
θ
,
φ
)
=
3
64
35
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
143
cos
5
θ
−
110
cos
3
θ
+
15
cos
θ
)
Y
7
−
1
(
θ
,
φ
)
=
1
64
105
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
429
cos
6
θ
−
495
cos
4
θ
+
135
cos
2
θ
−
5
)
Y
7
0
(
θ
,
φ
)
=
1
32
15
π
⋅
(
429
cos
7
θ
−
693
cos
5
θ
+
315
cos
3
θ
−
35
cos
θ
)
Y
7
1
(
θ
,
φ
)
=
−
1
64
105
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
429
cos
6
θ
−
495
cos
4
θ
+
135
cos
2
θ
−
5
)
Y
7
2
(
θ
,
φ
)
=
3
64
35
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
143
cos
5
θ
−
110
cos
3
θ
+
15
cos
θ
)
Y
7
3
(
θ
,
φ
)
=
−
3
64
35
2
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
143
cos
4
θ
−
66
cos
2
θ
+
3
)
Y
7
4
(
θ
,
φ
)
=
3
32
385
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
(
13
cos
3
θ
−
3
cos
θ
)
Y
7
5
(
θ
,
φ
)
=
−
3
64
385
2
π
⋅
e
5
i
φ
⋅
sin
5
θ
⋅
(
13
cos
2
θ
−
1
)
Y
7
6
(
θ
,
φ
)
=
3
64
5005
π
⋅
e
6
i
φ
⋅
sin
6
θ
⋅
cos
θ
Y
7
7
(
θ
,
φ
)
=
−
3
64
715
2
π
⋅
e
7
i
φ
⋅
sin
7
θ
{\displaystyle {\begin{aligned}Y_{7}^{-7}(\theta ,\varphi )&={3 \over 64}{\sqrt {715 \over 2\pi }}\cdot e^{-7i\varphi }\cdot \sin ^{7}\theta \\Y_{7}^{-6}(\theta ,\varphi )&={3 \over 64}{\sqrt {5005 \over \pi }}\cdot e^{-6i\varphi }\cdot \sin ^{6}\theta \cdot \cos \theta \\Y_{7}^{-5}(\theta ,\varphi )&={3 \over 64}{\sqrt {385 \over 2\pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \cdot (13\cos ^{2}\theta -1)\\Y_{7}^{-4}(\theta ,\varphi )&={3 \over 32}{\sqrt {385 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot (13\cos ^{3}\theta -3\cos \theta )\\Y_{7}^{-3}(\theta ,\varphi )&={3 \over 64}{\sqrt {35 \over 2\pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (143\cos ^{4}\theta -66\cos ^{2}\theta +3)\\Y_{7}^{-2}(\theta ,\varphi )&={3 \over 64}{\sqrt {35 \over \pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (143\cos ^{5}\theta -110\cos ^{3}\theta +15\cos \theta )\\Y_{7}^{-1}(\theta ,\varphi )&={1 \over 64}{\sqrt {105 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (429\cos ^{6}\theta -495\cos ^{4}\theta +135\cos ^{2}\theta -5)\\Y_{7}^{0}(\theta ,\varphi )&={1 \over 32}{\sqrt {15 \over \pi }}\cdot (429\cos ^{7}\theta -693\cos ^{5}\theta +315\cos ^{3}\theta -35\cos \theta )\\Y_{7}^{1}(\theta ,\varphi )&=-{1 \over 64}{\sqrt {105 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (429\cos ^{6}\theta -495\cos ^{4}\theta +135\cos ^{2}\theta -5)\\Y_{7}^{2}(\theta ,\varphi )&={3 \over 64}{\sqrt {35 \over \pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (143\cos ^{5}\theta -110\cos ^{3}\theta +15\cos \theta )\\Y_{7}^{3}(\theta ,\varphi )&=-{3 \over 64}{\sqrt {35 \over 2\pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (143\cos ^{4}\theta -66\cos ^{2}\theta +3)\\Y_{7}^{4}(\theta ,\varphi )&={3 \over 32}{\sqrt {385 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot (13\cos ^{3}\theta -3\cos \theta )\\Y_{7}^{5}(\theta ,\varphi )&=-{3 \over 64}{\sqrt {385 \over 2\pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \cdot (13\cos ^{2}\theta -1)\\Y_{7}^{6}(\theta ,\varphi )&={3 \over 64}{\sqrt {5005 \over \pi }}\cdot e^{6i\varphi }\cdot \sin ^{6}\theta \cdot \cos \theta \\Y_{7}^{7}(\theta ,\varphi )&=-{3 \over 64}{\sqrt {715 \over 2\pi }}\cdot e^{7i\varphi }\cdot \sin ^{7}\theta \end{aligned}}}
Y
8
−
8
(
θ
,
φ
)
=
3
256
12155
2
π
⋅
e
−
8
i
φ
⋅
sin
8
θ
Y
8
−
7
(
θ
,
φ
)
=
3
64
12155
2
π
⋅
e
−
7
i
φ
⋅
sin
7
θ
⋅
cos
θ
Y
8
−
6
(
θ
,
φ
)
=
1
128
7293
π
⋅
e
−
6
i
φ
⋅
sin
6
θ
⋅
(
15
cos
2
θ
−
1
)
Y
8
−
5
(
θ
,
φ
)
=
3
64
17017
2
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
⋅
(
5
cos
3
θ
−
cos
θ
)
Y
8
−
4
(
θ
,
φ
)
=
3
128
1309
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
(
65
cos
4
θ
−
26
cos
2
θ
+
1
)
Y
8
−
3
(
θ
,
φ
)
=
1
64
19635
2
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
39
cos
5
θ
−
26
cos
3
θ
+
3
cos
θ
)
Y
8
−
2
(
θ
,
φ
)
=
3
128
595
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
143
cos
6
θ
−
143
cos
4
θ
+
33
cos
2
θ
−
1
)
Y
8
−
1
(
θ
,
φ
)
=
3
64
17
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
715
cos
7
θ
−
1001
cos
5
θ
+
385
cos
3
θ
−
35
cos
θ
)
Y
8
0
(
θ
,
φ
)
=
1
256
17
π
⋅
(
6435
cos
8
θ
−
12012
cos
6
θ
+
6930
cos
4
θ
−
1260
cos
2
θ
+
35
)
Y
8
1
(
θ
,
φ
)
=
−
3
64
17
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
715
cos
7
θ
−
1001
cos
5
θ
+
385
cos
3
θ
−
35
cos
θ
)
Y
8
2
(
θ
,
φ
)
=
3
128
595
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
143
cos
6
θ
−
143
cos
4
θ
+
33
cos
2
θ
−
1
)
Y
8
3
(
θ
,
φ
)
=
−
1
64
19635
2
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
39
cos
5
θ
−
26
cos
3
θ
+
3
cos
θ
)
Y
8
4
(
θ
,
φ
)
=
3
128
1309
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
(
65
cos
4
θ
−
26
cos
2
θ
+
1
)
Y
8
5
(
θ
,
φ
)
=
−
3
64
17017
2
π
⋅
e
5
i
φ
⋅
sin
5
θ
⋅
(
5
cos
3
θ
−
cos
θ
)
Y
8
6
(
θ
,
φ
)
=
1
128
7293
π
⋅
e
6
i
φ
⋅
sin
6
θ
⋅
(
15
cos
2
θ
−
1
)
Y
8
7
(
θ
,
φ
)
=
−
3
64
12155
2
π
⋅
e
7
i
φ
⋅
sin
7
θ
⋅
cos
θ
Y
8
8
(
θ
,
φ
)
=
3
256
12155
2
π
⋅
e
8
i
φ
⋅
sin
8
θ
{\displaystyle {\begin{aligned}Y_{8}^{-8}(\theta ,\varphi )&={3 \over 256}{\sqrt {12155 \over 2\pi }}\cdot e^{-8i\varphi }\cdot \sin ^{8}\theta \\Y_{8}^{-7}(\theta ,\varphi )&={3 \over 64}{\sqrt {12155 \over 2\pi }}\cdot e^{-7i\varphi }\cdot \sin ^{7}\theta \cdot \cos \theta \\Y_{8}^{-6}(\theta ,\varphi )&={1 \over 128}{\sqrt {7293 \over \pi }}\cdot e^{-6i\varphi }\cdot \sin ^{6}\theta \cdot (15\cos ^{2}\theta -1)\\Y_{8}^{-5}(\theta ,\varphi )&={3 \over 64}{\sqrt {17017 \over 2\pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \cdot (5\cos ^{3}\theta -\cos \theta )\\Y_{8}^{-4}(\theta ,\varphi )&={3 \over 128}{\sqrt {1309 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot (65\cos ^{4}\theta -26\cos ^{2}\theta +1)\\Y_{8}^{-3}(\theta ,\varphi )&={1 \over 64}{\sqrt {19635 \over 2\pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (39\cos ^{5}\theta -26\cos ^{3}\theta +3\cos \theta )\\Y_{8}^{-2}(\theta ,\varphi )&={3 \over 128}{\sqrt {595 \over \pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (143\cos ^{6}\theta -143\cos ^{4}\theta +33\cos ^{2}\theta -1)\\Y_{8}^{-1}(\theta ,\varphi )&={3 \over 64}{\sqrt {17 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (715\cos ^{7}\theta -1001\cos ^{5}\theta +385\cos ^{3}\theta -35\cos \theta )\\Y_{8}^{0}(\theta ,\varphi )&={1 \over 256}{\sqrt {17 \over \pi }}\cdot (6435\cos ^{8}\theta -12012\cos ^{6}\theta +6930\cos ^{4}\theta -1260\cos ^{2}\theta +35)\\Y_{8}^{1}(\theta ,\varphi )&={-3 \over 64}{\sqrt {17 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (715\cos ^{7}\theta -1001\cos ^{5}\theta +385\cos ^{3}\theta -35\cos \theta )\\Y_{8}^{2}(\theta ,\varphi )&={3 \over 128}{\sqrt {595 \over \pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (143\cos ^{6}\theta -143\cos ^{4}\theta +33\cos ^{2}\theta -1)\\Y_{8}^{3}(\theta ,\varphi )&={-1 \over 64}{\sqrt {19635 \over 2\pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (39\cos ^{5}\theta -26\cos ^{3}\theta +3\cos \theta )\\Y_{8}^{4}(\theta ,\varphi )&={3 \over 128}{\sqrt {1309 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot (65\cos ^{4}\theta -26\cos ^{2}\theta +1)\\Y_{8}^{5}(\theta ,\varphi )&={-3 \over 64}{\sqrt {17017 \over 2\pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \cdot (5\cos ^{3}\theta -\cos \theta )\\Y_{8}^{6}(\theta ,\varphi )&={1 \over 128}{\sqrt {7293 \over \pi }}\cdot e^{6i\varphi }\cdot \sin ^{6}\theta \cdot (15\cos ^{2}\theta -1)\\Y_{8}^{7}(\theta ,\varphi )&={-3 \over 64}{\sqrt {12155 \over 2\pi }}\cdot e^{7i\varphi }\cdot \sin ^{7}\theta \cdot \cos \theta \\Y_{8}^{8}(\theta ,\varphi )&={3 \over 256}{\sqrt {12155 \over 2\pi }}\cdot e^{8i\varphi }\cdot \sin ^{8}\theta \end{aligned}}}
Y
9
−
9
(
θ
,
φ
)
=
1
512
230945
π
⋅
e
−
9
i
φ
⋅
sin
9
θ
Y
9
−
8
(
θ
,
φ
)
=
3
256
230945
2
π
⋅
e
−
8
i
φ
⋅
sin
8
θ
⋅
cos
θ
Y
9
−
7
(
θ
,
φ
)
=
3
512
13585
π
⋅
e
−
7
i
φ
⋅
sin
7
θ
⋅
(
17
cos
2
θ
−
1
)
Y
9
−
6
(
θ
,
φ
)
=
1
128
40755
π
⋅
e
−
6
i
φ
⋅
sin
6
θ
⋅
(
17
cos
3
θ
−
3
cos
θ
)
Y
9
−
5
(
θ
,
φ
)
=
3
256
2717
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
⋅
(
85
cos
4
θ
−
30
cos
2
θ
+
1
)
Y
9
−
4
(
θ
,
φ
)
=
3
128
95095
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
(
17
cos
5
θ
−
10
cos
3
θ
+
cos
θ
)
Y
9
−
3
(
θ
,
φ
)
=
1
256
21945
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
221
cos
6
θ
−
195
cos
4
θ
+
39
cos
2
θ
−
1
)
Y
9
−
2
(
θ
,
φ
)
=
3
128
1045
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
221
cos
7
θ
−
273
cos
5
θ
+
91
cos
3
θ
−
7
cos
θ
)
Y
9
−
1
(
θ
,
φ
)
=
3
256
95
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
2431
cos
8
θ
−
4004
cos
6
θ
+
2002
cos
4
θ
−
308
cos
2
θ
+
7
)
Y
9
0
(
θ
,
φ
)
=
1
256
19
π
⋅
(
12155
cos
9
θ
−
25740
cos
7
θ
+
18018
cos
5
θ
−
4620
cos
3
θ
+
315
cos
θ
)
Y
9
1
(
θ
,
φ
)
=
−
3
256
95
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
2431
cos
8
θ
−
4004
cos
6
θ
+
2002
cos
4
θ
−
308
cos
2
θ
+
7
)
Y
9
2
(
θ
,
φ
)
=
3
128
1045
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
221
cos
7
θ
−
273
cos
5
θ
+
91
cos
3
θ
−
7
cos
θ
)
Y
9
3
(
θ
,
φ
)
=
−
1
256
21945
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
221
cos
6
θ
−
195
cos
4
θ
+
39
cos
2
θ
−
1
)
Y
9
4
(
θ
,
φ
)
=
3
128
95095
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
(
17
cos
5
θ
−
10
cos
3
θ
+
cos
θ
)
Y
9
5
(
θ
,
φ
)
=
−
3
256
2717
π
⋅
e
5
i
φ
⋅
sin
5
θ
⋅
(
85
cos
4
θ
−
30
cos
2
θ
+
1
)
Y
9
6
(
θ
,
φ
)
=
1
128
40755
π
⋅
e
6
i
φ
⋅
sin
6
θ
⋅
(
17
cos
3
θ
−
3
cos
θ
)
Y
9
7
(
θ
,
φ
)
=
−
3
512
13585
π
⋅
e
7
i
φ
⋅
sin
7
θ
⋅
(
17
cos
2
θ
−
1
)
Y
9
8
(
θ
,
φ
)
=
3
256
230945
2
π
⋅
e
8
i
φ
⋅
sin
8
θ
⋅
cos
θ
Y
9
9
(
θ
,
φ
)
=
−
1
512
230945
π
⋅
e
9
i
φ
⋅
sin
9
θ
{\displaystyle {\begin{aligned}Y_{9}^{-9}(\theta ,\varphi )&={1 \over 512}{\sqrt {230945 \over \pi }}\cdot e^{-9i\varphi }\cdot \sin ^{9}\theta \\Y_{9}^{-8}(\theta ,\varphi )&={3 \over 256}{\sqrt {230945 \over 2\pi }}\cdot e^{-8i\varphi }\cdot \sin ^{8}\theta \cdot \cos \theta \\Y_{9}^{-7}(\theta ,\varphi )&={3 \over 512}{\sqrt {13585 \over \pi }}\cdot e^{-7i\varphi }\cdot \sin ^{7}\theta \cdot (17\cos ^{2}\theta -1)\\Y_{9}^{-6}(\theta ,\varphi )&={1 \over 128}{\sqrt {40755 \over \pi }}\cdot e^{-6i\varphi }\cdot \sin ^{6}\theta \cdot (17\cos ^{3}\theta -3\cos \theta )\\Y_{9}^{-5}(\theta ,\varphi )&={3 \over 256}{\sqrt {2717 \over \pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \cdot (85\cos ^{4}\theta -30\cos ^{2}\theta +1)\\Y_{9}^{-4}(\theta ,\varphi )&={3 \over 128}{\sqrt {95095 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot (17\cos ^{5}\theta -10\cos ^{3}\theta +\cos \theta )\\Y_{9}^{-3}(\theta ,\varphi )&={1 \over 256}{\sqrt {21945 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (221\cos ^{6}\theta -195\cos ^{4}\theta +39\cos ^{2}\theta -1)\\Y_{9}^{-2}(\theta ,\varphi )&={3 \over 128}{\sqrt {1045 \over \pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (221\cos ^{7}\theta -273\cos ^{5}\theta +91\cos ^{3}\theta -7\cos \theta )\\Y_{9}^{-1}(\theta ,\varphi )&={3 \over 256}{\sqrt {95 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (2431\cos ^{8}\theta -4004\cos ^{6}\theta +2002\cos ^{4}\theta -308\cos ^{2}\theta +7)\\Y_{9}^{0}(\theta ,\varphi )&={1 \over 256}{\sqrt {19 \over \pi }}\cdot (12155\cos ^{9}\theta -25740\cos ^{7}\theta +18018\cos ^{5}\theta -4620\cos ^{3}\theta +315\cos \theta )\\Y_{9}^{1}(\theta ,\varphi )&={-3 \over 256}{\sqrt {95 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (2431\cos ^{8}\theta -4004\cos ^{6}\theta +2002\cos ^{4}\theta -308\cos ^{2}\theta +7)\\Y_{9}^{2}(\theta ,\varphi )&={3 \over 128}{\sqrt {1045 \over \pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (221\cos ^{7}\theta -273\cos ^{5}\theta +91\cos ^{3}\theta -7\cos \theta )\\Y_{9}^{3}(\theta ,\varphi )&={-1 \over 256}{\sqrt {21945 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (221\cos ^{6}\theta -195\cos ^{4}\theta +39\cos ^{2}\theta -1)\\Y_{9}^{4}(\theta ,\varphi )&={3 \over 128}{\sqrt {95095 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot (17\cos ^{5}\theta -10\cos ^{3}\theta +\cos \theta )\\Y_{9}^{5}(\theta ,\varphi )&={-3 \over 256}{\sqrt {2717 \over \pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \cdot (85\cos ^{4}\theta -30\cos ^{2}\theta +1)\\Y_{9}^{6}(\theta ,\varphi )&={1 \over 128}{\sqrt {40755 \over \pi }}\cdot e^{6i\varphi }\cdot \sin ^{6}\theta \cdot (17\cos ^{3}\theta -3\cos \theta )\\Y_{9}^{7}(\theta ,\varphi )&={-3 \over 512}{\sqrt {13585 \over \pi }}\cdot e^{7i\varphi }\cdot \sin ^{7}\theta \cdot (17\cos ^{2}\theta -1)\\Y_{9}^{8}(\theta ,\varphi )&={3 \over 256}{\sqrt {230945 \over 2\pi }}\cdot e^{8i\varphi }\cdot \sin ^{8}\theta \cdot \cos \theta \\Y_{9}^{9}(\theta ,\varphi )&={-1 \over 512}{\sqrt {230945 \over \pi }}\cdot e^{9i\varphi }\cdot \sin ^{9}\theta \end{aligned}}}
Y
10
−
10
(
θ
,
φ
)
=
1
1024
969969
π
⋅
e
−
10
i
φ
⋅
sin
10
θ
Y
10
−
9
(
θ
,
φ
)
=
1
512
4849845
π
⋅
e
−
9
i
φ
⋅
sin
9
θ
⋅
cos
θ
Y
10
−
8
(
θ
,
φ
)
=
1
512
255255
2
π
⋅
e
−
8
i
φ
⋅
sin
8
θ
⋅
(
19
cos
2
θ
−
1
)
Y
10
−
7
(
θ
,
φ
)
=
3
512
85085
π
⋅
e
−
7
i
φ
⋅
sin
7
θ
⋅
(
19
cos
3
θ
−
3
cos
θ
)
Y
10
−
6
(
θ
,
φ
)
=
3
1024
5005
π
⋅
e
−
6
i
φ
⋅
sin
6
θ
⋅
(
323
cos
4
θ
−
102
cos
2
θ
+
3
)
Y
10
−
5
(
θ
,
φ
)
=
3
256
1001
π
⋅
e
−
5
i
φ
⋅
sin
5
θ
⋅
(
323
cos
5
θ
−
170
cos
3
θ
+
15
cos
θ
)
Y
10
−
4
(
θ
,
φ
)
=
3
256
5005
2
π
⋅
e
−
4
i
φ
⋅
sin
4
θ
⋅
(
323
cos
6
θ
−
255
cos
4
θ
+
45
cos
2
θ
−
1
)
Y
10
−
3
(
θ
,
φ
)
=
3
256
5005
π
⋅
e
−
3
i
φ
⋅
sin
3
θ
⋅
(
323
cos
7
θ
−
357
cos
5
θ
+
105
cos
3
θ
−
7
cos
θ
)
Y
10
−
2
(
θ
,
φ
)
=
3
512
385
2
π
⋅
e
−
2
i
φ
⋅
sin
2
θ
⋅
(
4199
cos
8
θ
−
6188
cos
6
θ
+
2730
cos
4
θ
−
364
cos
2
θ
+
7
)
Y
10
−
1
(
θ
,
φ
)
=
1
256
1155
2
π
⋅
e
−
i
φ
⋅
sin
θ
⋅
(
4199
cos
9
θ
−
7956
cos
7
θ
+
4914
cos
5
θ
−
1092
cos
3
θ
+
63
cos
θ
)
Y
10
0
(
θ
,
φ
)
=
1
512
21
π
⋅
(
46189
cos
10
θ
−
109395
cos
8
θ
+
90090
cos
6
θ
−
30030
cos
4
θ
+
3465
cos
2
θ
−
63
)
Y
10
1
(
θ
,
φ
)
=
−
1
256
1155
2
π
⋅
e
i
φ
⋅
sin
θ
⋅
(
4199
cos
9
θ
−
7956
cos
7
θ
+
4914
cos
5
θ
−
1092
cos
3
θ
+
63
cos
θ
)
Y
10
2
(
θ
,
φ
)
=
3
512
385
2
π
⋅
e
2
i
φ
⋅
sin
2
θ
⋅
(
4199
cos
8
θ
−
6188
cos
6
θ
+
2730
cos
4
θ
−
364
cos
2
θ
+
7
)
Y
10
3
(
θ
,
φ
)
=
−
3
256
5005
π
⋅
e
3
i
φ
⋅
sin
3
θ
⋅
(
323
cos
7
θ
−
357
cos
5
θ
+
105
cos
3
θ
−
7
cos
θ
)
Y
10
4
(
θ
,
φ
)
=
3
256
5005
2
π
⋅
e
4
i
φ
⋅
sin
4
θ
⋅
(
323
cos
6
θ
−
255
cos
4
θ
+
45
cos
2
θ
−
1
)
Y
10
5
(
θ
,
φ
)
=
−
3
256
1001
π
⋅
e
5
i
φ
⋅
sin
5
θ
⋅
(
323
cos
5
θ
−
170
cos
3
θ
+
15
cos
θ
)
Y
10
6
(
θ
,
φ
)
=
3
1024
5005
π
⋅
e
6
i
φ
⋅
sin
6
θ
⋅
(
323
cos
4
θ
−
102
cos
2
θ
+
3
)
Y
10
7
(
θ
,
φ
)
=
−
3
512
85085
π
⋅
e
7
i
φ
⋅
sin
7
θ
⋅
(
19
cos
3
θ
−
3
cos
θ
)
Y
10
8
(
θ
,
φ
)
=
1
512
255255
2
π
⋅
e
8
i
φ
⋅
sin
8
θ
⋅
(
19
cos
2
θ
−
1
)
Y
10
9
(
θ
,
φ
)
=
−
1
512
4849845
π
⋅
e
9
i
φ
⋅
sin
9
θ
⋅
cos
θ
Y
10
10
(
θ
,
φ
)
=
1
1024
969969
π
⋅
e
10
i
φ
⋅
sin
10
θ
{\displaystyle {\begin{aligned}Y_{10}^{-10}(\theta ,\varphi )&={1 \over 1024}{\sqrt {969969 \over \pi }}\cdot e^{-10i\varphi }\cdot \sin ^{10}\theta \\Y_{10}^{-9}(\theta ,\varphi )&={1 \over 512}{\sqrt {4849845 \over \pi }}\cdot e^{-9i\varphi }\cdot \sin ^{9}\theta \cdot \cos \theta \\Y_{10}^{-8}(\theta ,\varphi )&={1 \over 512}{\sqrt {255255 \over 2\pi }}\cdot e^{-8i\varphi }\cdot \sin ^{8}\theta \cdot (19\cos ^{2}\theta -1)\\Y_{10}^{-7}(\theta ,\varphi )&={3 \over 512}{\sqrt {85085 \over \pi }}\cdot e^{-7i\varphi }\cdot \sin ^{7}\theta \cdot (19\cos ^{3}\theta -3\cos \theta )\\Y_{10}^{-6}(\theta ,\varphi )&={3 \over 1024}{\sqrt {5005 \over \pi }}\cdot e^{-6i\varphi }\cdot \sin ^{6}\theta \cdot (323\cos ^{4}\theta -102\cos ^{2}\theta +3)\\Y_{10}^{-5}(\theta ,\varphi )&={3 \over 256}{\sqrt {1001 \over \pi }}\cdot e^{-5i\varphi }\cdot \sin ^{5}\theta \cdot (323\cos ^{5}\theta -170\cos ^{3}\theta +15\cos \theta )\\Y_{10}^{-4}(\theta ,\varphi )&={3 \over 256}{\sqrt {5005 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta \cdot (323\cos ^{6}\theta -255\cos ^{4}\theta +45\cos ^{2}\theta -1)\\Y_{10}^{-3}(\theta ,\varphi )&={3 \over 256}{\sqrt {5005 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot (323\cos ^{7}\theta -357\cos ^{5}\theta +105\cos ^{3}\theta -7\cos \theta )\\Y_{10}^{-2}(\theta ,\varphi )&={3 \over 512}{\sqrt {385 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (4199\cos ^{8}\theta -6188\cos ^{6}\theta +2730\cos ^{4}\theta -364\cos ^{2}\theta +7)\\Y_{10}^{-1}(\theta ,\varphi )&={1 \over 256}{\sqrt {1155 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (4199\cos ^{9}\theta -7956\cos ^{7}\theta +4914\cos ^{5}\theta -1092\cos ^{3}\theta +63\cos \theta )\\Y_{10}^{0}(\theta ,\varphi )&={1 \over 512}{\sqrt {21 \over \pi }}\cdot (46189\cos ^{10}\theta -109395\cos ^{8}\theta +90090\cos ^{6}\theta -30030\cos ^{4}\theta +3465\cos ^{2}\theta -63)\\Y_{10}^{1}(\theta ,\varphi )&={-1 \over 256}{\sqrt {1155 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (4199\cos ^{9}\theta -7956\cos ^{7}\theta +4914\cos ^{5}\theta -1092\cos ^{3}\theta +63\cos \theta )\\Y_{10}^{2}(\theta ,\varphi )&={3 \over 512}{\sqrt {385 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot (4199\cos ^{8}\theta -6188\cos ^{6}\theta +2730\cos ^{4}\theta -364\cos ^{2}\theta +7)\\Y_{10}^{3}(\theta ,\varphi )&={-3 \over 256}{\sqrt {5005 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \cdot (323\cos ^{7}\theta -357\cos ^{5}\theta +105\cos ^{3}\theta -7\cos \theta )\\Y_{10}^{4}(\theta ,\varphi )&={3 \over 256}{\sqrt {5005 \over 2\pi }}\cdot e^{4i\varphi }\cdot \sin ^{4}\theta \cdot (323\cos ^{6}\theta -255\cos ^{4}\theta +45\cos ^{2}\theta -1)\\Y_{10}^{5}(\theta ,\varphi )&={-3 \over 256}{\sqrt {1001 \over \pi }}\cdot e^{5i\varphi }\cdot \sin ^{5}\theta \cdot (323\cos ^{5}\theta -170\cos ^{3}\theta +15\cos \theta )\\Y_{10}^{6}(\theta ,\varphi )&={3 \over 1024}{\sqrt {5005 \over \pi }}\cdot e^{6i\varphi }\cdot \sin ^{6}\theta \cdot (323\cos ^{4}\theta -102\cos ^{2}\theta +3)\\Y_{10}^{7}(\theta ,\varphi )&={-3 \over 512}{\sqrt {85085 \over \pi }}\cdot e^{7i\varphi }\cdot \sin ^{7}\theta \cdot (19\cos ^{3}\theta -3\cos \theta )\\Y_{10}^{8}(\theta ,\varphi )&={1 \over 512}{\sqrt {255255 \over 2\pi }}\cdot e^{8i\varphi }\cdot \sin ^{8}\theta \cdot (19\cos ^{2}\theta -1)\\Y_{10}^{9}(\theta ,\varphi )&={-1 \over 512}{\sqrt {4849845 \over \pi }}\cdot e^{9i\varphi }\cdot \sin ^{9}\theta \cdot \cos \theta \\Y_{10}^{10}(\theta ,\varphi )&={1 \over 1024}{\sqrt {969969 \over \pi }}\cdot e^{10i\varphi }\cdot \sin ^{10}\theta \end{aligned}}}
[ ред. | ред. код ] Нижче комплекснозначні сферичні гармоніки представлені на 2D графіках з азимутальним кутом,
φ
{\displaystyle \varphi }
θ
{\displaystyle \theta }
амплітуді сферичної гармоніки, а сам колір представляє собою фазу .
Набір зображень комплекснозначних сферичних гармонік, представлених у вигляді двовимірних карт по
θ
,
φ
{\displaystyle \theta ,\varphi }
Нижче комплексні сферичні гармоніки представлені у вигляді двовимірної карти на сфері. Величина сферичної гармоніки при певних полярних і азимутальних кутах представлена насиченістю кольору в цій точці, а фаза представлена кольором у цій точці.
Набір зображень комплексних сферичних гармонік на сфері [ ред. | ред. код ] Нижче на графіках амплітуді сферичної гармоніки під конкретним полярним і азимутальним кутами відповідає відстань від центру умовної сфери (радіус), а фазі гармоніки відповідає колір у цій точці.
Набір графіків комплексних сферичних гармонік, представлених на сфері із амплітудою, як радіусом точки Для кожної дійсної сферичної гармоніки також наведено відповідний атомний орбітальний символ (s , p , d , f ).[ 2] [ 3]
Для ℓ = 0, …, 3 див. також[ 4] [ 5]
Y
00
=
s
=
Y
0
0
=
1
2
1
π
{\displaystyle Y_{00}=s=Y_{0}^{0}={\frac {1}{2}}{\sqrt {\frac {1}{\pi }}}}
Y
1
,
−
1
=
p
y
=
i
1
2
(
Y
1
−
1
+
Y
1
1
)
=
3
4
π
⋅
y
r
Y
1
,
0
=
p
z
=
Y
1
0
=
3
4
π
⋅
z
r
Y
1
,
1
=
p
x
=
1
2
(
Y
1
−
1
−
Y
1
1
)
=
3
4
π
⋅
x
r
{\displaystyle {\begin{aligned}Y_{1,-1}&=p_{y}=i{\sqrt {\frac {1}{2}}}\left(Y_{1}^{-1}+Y_{1}^{1}\right)={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {y}{r}}\\Y_{1,0}&=p_{z}=Y_{1}^{0}={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {z}{r}}\\Y_{1,1}&=p_{x}={\sqrt {\frac {1}{2}}}\left(Y_{1}^{-1}-Y_{1}^{1}\right)={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {x}{r}}\end{aligned}}}
Y
2
,
−
2
=
d
x
y
=
i
1
2
(
Y
2
−
2
−
Y
2
2
)
=
1
2
15
π
⋅
x
y
r
2
Y
2
,
−
1
=
d
y
z
=
i
1
2
(
Y
2
−
1
+
Y
2
1
)
=
1
2
15
π
⋅
y
⋅
z
r
2
Y
2
,
0
=
d
z
2
=
Y
2
0
=
1
4
5
π
⋅
3
z
2
−
r
2
r
2
Y
2
,
1
=
d
x
z
=
1
2
(
Y
2
−
1
−
Y
2
1
)
=
1
2
15
π
⋅
x
⋅
z
r
2
Y
2
,
2
=
d
x
2
−
y
2
=
1
2
(
Y
2
−
2
+
Y
2
2
)
=
1
4
15
π
⋅
x
2
−
y
2
r
2
{\displaystyle {\begin{aligned}Y_{2,-2}&=d_{xy}=i{\sqrt {\frac {1}{2}}}\left(Y_{2}^{-2}-Y_{2}^{2}\right)={\frac {1}{2}}{\sqrt {\frac {15}{\pi }}}\cdot {\frac {xy}{r^{2}}}\\Y_{2,-1}&=d_{yz}=i{\sqrt {\frac {1}{2}}}\left(Y_{2}^{-1}+Y_{2}^{1}\right)={\frac {1}{2}}{\sqrt {\frac {15}{\pi }}}\cdot {\frac {y\cdot z}{r^{2}}}\\Y_{2,0}&=d_{z^{2}}=Y_{2}^{0}={\frac {1}{4}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {3z^{2}-r^{2}}{r^{2}}}\\Y_{2,1}&=d_{xz}={\sqrt {\frac {1}{2}}}\left(Y_{2}^{-1}-Y_{2}^{1}\right)={\frac {1}{2}}{\sqrt {\frac {15}{\pi }}}\cdot {\frac {x\cdot z}{r^{2}}}\\Y_{2,2}&=d_{x^{2}-y^{2}}={\sqrt {\frac {1}{2}}}\left(Y_{2}^{-2}+Y_{2}^{2}\right)={\frac {1}{4}}{\sqrt {\frac {15}{\pi }}}\cdot {\frac {x^{2}-y^{2}}{r^{2}}}\end{aligned}}}
Y
3
,
−
3
=
f
y
(
3
x
2
−
y
2
)
=
i
1
2
(
Y
3
−
3
+
Y
3
3
)
=
1
4
35
2
π
⋅
y
(
3
x
2
−
y
2
)
r
3
Y
3
,
−
2
=
f
x
y
z
=
i
1
2
(
Y
3
−
2
−
Y
3
2
)
=
1
2
105
π
⋅
x
y
⋅
z
r
3
Y
3
,
−
1
=
f
y
z
2
=
i
1
2
(
Y
3
−
1
+
Y
3
1
)
=
1
4
21
2
π
⋅
y
⋅
(
5
z
2
−
r
2
)
r
3
Y
3
,
0
=
f
z
3
=
Y
3
0
=
1
4
7
π
⋅
5
z
3
−
3
z
r
2
r
3
Y
3
,
1
=
f
x
z
2
=
1
2
(
Y
3
−
1
−
Y
3
1
)
=
1
4
21
2
π
⋅
x
⋅
(
5
z
2
−
r
2
)
r
3
Y
3
,
2
=
f
z
(
x
2
−
y
2
)
=
1
2
(
Y
3
−
2
+
Y
3
2
)
=
1
4
105
π
⋅
(
x
2
−
y
2
)
⋅
z
r
3
Y
3
,
3
=
f
x
(
x
2
−
3
y
2
)
=
1
2
(
Y
3
−
3
−
Y
3
3
)
=
1
4
35
2
π
⋅
x
(
x
2
−
3
y
2
)
r
3
{\displaystyle {\begin{aligned}Y_{3,-3}&=f_{y(3x^{2}-y^{2})}=i{\sqrt {\frac {1}{2}}}\left(Y_{3}^{-3}+Y_{3}^{3}\right)={\frac {1}{4}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {y\left(3x^{2}-y^{2}\right)}{r^{3}}}\\Y_{3,-2}&=f_{xyz}=i{\sqrt {\frac {1}{2}}}\left(Y_{3}^{-2}-Y_{3}^{2}\right)={\frac {1}{2}}{\sqrt {\frac {105}{\pi }}}\cdot {\frac {xy\cdot z}{r^{3}}}\\Y_{3,-1}&=f_{yz^{2}}=i{\sqrt {\frac {1}{2}}}\left(Y_{3}^{-1}+Y_{3}^{1}\right)={\frac {1}{4}}{\sqrt {\frac {21}{2\pi }}}\cdot {\frac {y\cdot (5z^{2}-r^{2})}{r^{3}}}\\Y_{3,0}&=f_{z^{3}}=Y_{3}^{0}={\frac {1}{4}}{\sqrt {\frac {7}{\pi }}}\cdot {\frac {5z^{3}-3zr^{2}}{r^{3}}}\\Y_{3,1}&=f_{xz^{2}}={\sqrt {\frac {1}{2}}}\left(Y_{3}^{-1}-Y_{3}^{1}\right)={\frac {1}{4}}{\sqrt {\frac {21}{2\pi }}}\cdot {\frac {x\cdot (5z^{2}-r^{2})}{r^{3}}}\\Y_{3,2}&=f_{z(x^{2}-y^{2})}={\sqrt {\frac {1}{2}}}\left(Y_{3}^{-2}+Y_{3}^{2}\right)={\frac {1}{4}}{\sqrt {\frac {105}{\pi }}}\cdot {\frac {\left(x^{2}-y^{2}\right)\cdot z}{r^{3}}}\\Y_{3,3}&=f_{x(x^{2}-3y^{2})}={\sqrt {\frac {1}{2}}}\left(Y_{3}^{-3}-Y_{3}^{3}\right)={\frac {1}{4}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {x\left(x^{2}-3y^{2}\right)}{r^{3}}}\end{aligned}}}
Y
4
,
−
4
=
i
1
2
(
Y
4
−
4
−
Y
4
4
)
=
3
4
35
π
⋅
x
y
(
x
2
−
y
2
)
r
4
Y
4
,
−
3
=
i
1
2
(
Y
4
−
3
+
Y
4
3
)
=
3
4
35
2
π
⋅
y
(
3
x
2
−
y
2
)
⋅
z
r
4
Y
4
,
−
2
=
i
1
2
(
Y
4
−
2
−
Y
4
2
)
=
3
4
5
π
⋅
x
y
⋅
(
7
z
2
−
r
2
)
r
4
Y
4
,
−
1
=
i
1
2
(
Y
4
−
1
+
Y
4
1
)
=
3
4
5
2
π
⋅
y
⋅
(
7
z
3
−
3
z
r
2
)
r
4
Y
4
,
0
=
Y
4
0
=
3
16
1
π
⋅
35
z
4
−
30
z
2
r
2
+
3
r
4
r
4
Y
4
,
1
=
1
2
(
Y
4
−
1
−
Y
4
1
)
=
3
4
5
2
π
⋅
x
⋅
(
7
z
3
−
3
z
r
2
)
r
4
Y
4
,
2
=
1
2
(
Y
4
−
2
+
Y
4
2
)
=
3
8
5
π
⋅
(
x
2
−
y
2
)
⋅
(
7
z
2
−
r
2
)
r
4
Y
4
,
3
=
1
2
(
Y
4
−
3
−
Y
4
3
)
=
3
4
35
2
π
⋅
x
(
x
2
−
3
y
2
)
⋅
z
r
4
Y
4
,
4
=
1
2
(
Y
4
−
4
+
Y
4
4
)
=
3
16
35
π
⋅
x
2
(
x
2
−
3
y
2
)
−
y
2
(
3
x
2
−
y
2
)
r
4
{\displaystyle {\begin{aligned}Y_{4,-4}&=i{\sqrt {\frac {1}{2}}}\left(Y_{4}^{-4}-Y_{4}^{4}\right)={\frac {3}{4}}{\sqrt {\frac {35}{\pi }}}\cdot {\frac {xy\left(x^{2}-y^{2}\right)}{r^{4}}}\\Y_{4,-3}&=i{\sqrt {\frac {1}{2}}}\left(Y_{4}^{-3}+Y_{4}^{3}\right)={\frac {3}{4}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {y(3x^{2}-y^{2})\cdot z}{r^{4}}}\\Y_{4,-2}&=i{\sqrt {\frac {1}{2}}}\left(Y_{4}^{-2}-Y_{4}^{2}\right)={\frac {3}{4}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {xy\cdot (7z^{2}-r^{2})}{r^{4}}}\\Y_{4,-1}&=i{\sqrt {\frac {1}{2}}}\left(Y_{4}^{-1}+Y_{4}^{1}\right)={\frac {3}{4}}{\sqrt {\frac {5}{2\pi }}}\cdot {\frac {y\cdot (7z^{3}-3zr^{2})}{r^{4}}}\\Y_{4,0}&=Y_{4}^{0}={\frac {3}{16}}{\sqrt {\frac {1}{\pi }}}\cdot {\frac {35z^{4}-30z^{2}r^{2}+3r^{4}}{r^{4}}}\\Y_{4,1}&={\sqrt {\frac {1}{2}}}\left(Y_{4}^{-1}-Y_{4}^{1}\right)={\frac {3}{4}}{\sqrt {\frac {5}{2\pi }}}\cdot {\frac {x\cdot (7z^{3}-3zr^{2})}{r^{4}}}\\Y_{4,2}&={\sqrt {\frac {1}{2}}}\left(Y_{4}^{-2}+Y_{4}^{2}\right)={\frac {3}{8}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {(x^{2}-y^{2})\cdot (7z^{2}-r^{2})}{r^{4}}}\\Y_{4,3}&={\sqrt {\frac {1}{2}}}\left(Y_{4}^{-3}-Y_{4}^{3}\right)={\frac {3}{4}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {x(x^{2}-3y^{2})\cdot z}{r^{4}}}\\Y_{4,4}&={\sqrt {\frac {1}{2}}}\left(Y_{4}^{-4}+Y_{4}^{4}\right)={\frac {3}{16}}{\sqrt {\frac {35}{\pi }}}\cdot {\frac {x^{2}\left(x^{2}-3y^{2}\right)-y^{2}\left(3x^{2}-y^{2}\right)}{r^{4}}}\\{}\end{aligned}}}
Нижче дійснозначні сферичні гармоніки представлені на 2D графіках з азимутальним кутом,
φ
{\displaystyle \varphi }
θ
{\displaystyle \theta }
Набір зображень дійсних сферичних гармонік, представлених у вигляді двовимірних карт від кутових змінних Нижче дійсні сферичні гармоніки зображені на сфері. Амплітуді сферичної гармоніки при певних полярних і азимутальних кутах відповідає насиченість кольору в цій точці, а фаза — кольору у цій точці.
Набір графіків сферичних гармонік, зображений на двовимірній сфері Нижче дійсні сферичні гармоніки зображені на сфері, причому амплітуді сферичної гармоніки під конкретним полярним і азимутальним кутами відповідає відстань від центру умовної сфери, а фаза зображена кольором у цій точці.
Набір графіків дійсних сферичних гармонік, представлених на сфері з амплітудою як радіусом [ ред. | ред. код ] Нижче дійсні сферичні гармоніки представлені на сфері, де амплітуді сферичної гармоніки (величині і знаку) під певним полярним і азимутальним кутом відповідає висота графіка в цій точці відносно поверхні сфери фіксованого радіуса (над або під поверхнею сфери в залежності від знаку амплітуди). Додатково амплітуді відповідає насиченість кольору в даній точці. Фаза зображена кольором.
Набір графіків дійсних сферичних гармонік, представлених на сфері з амплітудою, як висотою від поверхні сфери і насиченістю кольору