Тестові функції для оптимізації

Тестові функції для оптимізації

Тестові функції для оптимізації у Вікісховищі

У прикладній математиці тестові функції для оптимізації (штучні ландшафти) — нелінійні функції, які використовують для оцінки характеристик алгоритмів оптимізації, таких як: швидкість збіжності; точність; грубість; загальні характеристики.

Нижче наведені деякі функції тестування оптимізаційних алгоритмів, що дозволяють отримати уявлення про різні характерні ситуації, з якими стикаються алгоритми оптимізації при вирішенні задач такого роду. У першій частині наведені функції для тестування алгоритмів пошуку глобального мінімуму (максимуму). У другій частині функції з відповідними фронтами для алгоритмів багатокритеріальної оптимізації.

Штучні ландшафти, наведені для тестування оптимізаційних алгоритмів, взяті з декількох джерел (див. Посилання).

Загальний вигляд рівняння, графік цільової функції, межі змінних об'єкта і координати глобального мінімуму наведені в таблиці.

Функції для алгоритмів пошуку глобального мінімуму

Назва / Рисунок	Формула	Мінімум	Область пошуку
Ackley's function	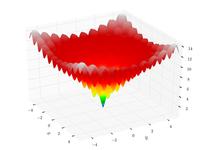$f(x,y)=-20\exp \left(-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right)$ $-\exp \left(0.5\left(\cos \left(2\pi x\right)+\cos \left(2\pi y\right)\right)\right)+e+20$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Sphere function	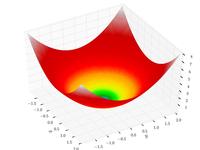$f({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}$	$f(0,\dots ,0)=0$	$-\infty \leq x_{i}\leq \infty$, $1\leq i\leq n$
Функція Розенброка	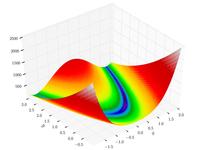$f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right]$	${\text{Min}}={\begin{cases}n=2&\rightarrow \quad f(1,1)=0,\\n=3&\rightarrow \quad f(1,1,1)=0,\\n>3&\rightarrow \quad f\left(\underbrace {1,\dots ,1} _{(n){\text{ times}}}\right)=0\\\end{cases}}$	$-\infty \leq x_{i}\leq \infty$, $1\leq i\leq n$
Beale's function	$f(x,y)=\left(1.5-x+xy\right)^{2}+\left(2.25-x+xy^{2}\right)^{2}$ $+\left(2.625-x+xy^{3}\right)^{2}$	$f(3,0.5)=0$	$-4.5\leq x,y\leq 4.5$
Goldstein–Price function	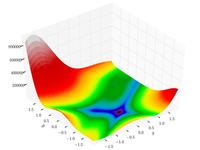$f(x,y)=$ $\left(1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right)$ $\left(30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right)$	$f(0,-1)=3$	$-2\leq x,y\leq 2$
Booth's function	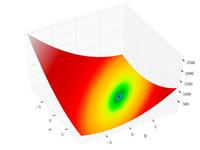$f(x,y)=\left(x+2y-7\right)^{2}+\left(2x+y-5\right)^{2}$	$f(1,3)=0$	$-10\leq x,y\leq 10$
Bukin function N.6	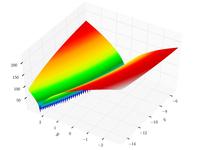$f(x,y)=100{\sqrt {\left|y-0.01x^{2}\right|}}+0.01\left|x+10\right|.\quad$	$f(-10,1)=0$	$-15\leq x\leq -5$, $-3\leq y\leq 3$
Matyas function	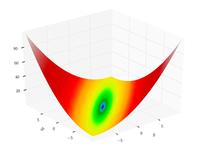$f(x,y)=0.26\left(x^{2}+y^{2}\right)-0.48xy$	$f(0,0)=0$	$-10\leq x,y\leq 10$
Lévi function N.13	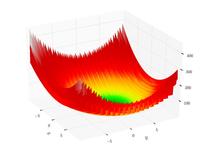$f(x,y)=\sin ^{2}\left(3\pi x\right)+\left(x-1\right)^{2}\left(1+\sin ^{2}\left(3\pi y\right)\right)$ $+\left(y-1\right)^{2}\left(1+\sin ^{2}\left(2\pi y\right)\right)$	$f(1,1)=0$	$-10\leq x,y\leq 10$
Three-hump camel function	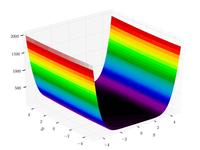$f(x,y)=2x^{2}-1.05x^{4}+{\frac {x^{6}}{6}}+xy+y^{2}$	$f(0,0)=0$	$-5\leq x,y\leq 5$
Easom function	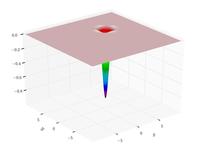$f(x,y)=-\cos \left(x\right)\cos \left(y\right)$ $\exp \left(-\left(\left(x-\pi \right)^{2}+\left(y-\pi \right)^{2}\right)\right)$	$f(\pi ,\pi )=-1$	$-100\leq x,y\leq 100$
Cross-in-tray function	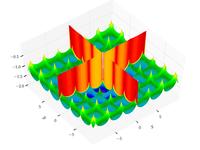$f(x,y)=-0.0001$ $\left(\left|\sin \left(x\right)\sin \left(y\right)\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right)^{0.1}$	${\text{Min}}={\begin{cases}f\left(1.34941,-1.34941\right)&=-2.06261\\f\left(1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,-1.34941\right)&=-2.06261\\\end{cases}}$	$-10\leq x,y\leq 10$
Eggholder function	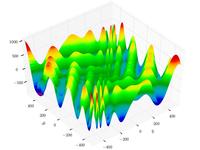$f(x,y)=-\left(y+47\right)\sin \left({\sqrt {\left|{\frac {x}{2}}+\left(y+47\right)\right|}}\right)$ $-x\sin \left({\sqrt {\left|x-\left(y+47\right)\right|}}\right)$	$f(512,404.2319)=-959.6407$	$-512\leq x,y\leq 512$
Hölder table function	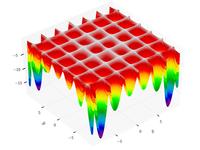$f(x,y)=-\left|\sin \left(x\right)\cos \left(y\right)\exp \left(\left|1-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|$	${\text{Min}}={\begin{cases}f\left(8.05502,9.66459\right)&=-19.2085\\f\left(-8.05502,9.66459\right)&=-19.2085\\f\left(8.05502,-9.66459\right)&=-19.2085\\f\left(-8.05502,-9.66459\right)&=-19.2085\end{cases}}$	$-10\leq x,y\leq 10$
McCormick function	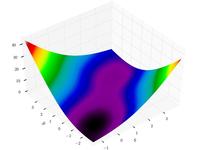$f(x,y)=\sin \left(x+y\right)+\left(x-y\right)^{2}-1.5x+2.5y+1$	$f(-0.54719,-1.54719)=-1.9133$	$-1.5\leq x\leq 4$, $-3\leq y\leq 4$
Schaffer function N. 2	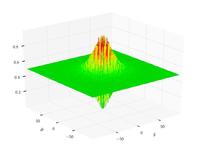$f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left(1+0.001\left(x^{2}+y^{2}\right)\right)^{2}}}$	$f(0,0)=0$	$-100\leq x,y\leq 100$
Schaffer function N. 4	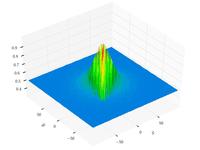$f(x,y)=0.5+{\frac {\cos ^{2}\left(\sin \left(\left|x^{2}-y^{2}\right|\right)\right)-0.5}{\left(1+0.001\left(x^{2}+y^{2}\right)\right)^{2}}}$	$f(0,1.25313)=0.292579$	$-100\leq x,y\leq 100$
Styblinski–Tang function	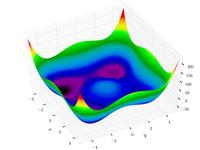$f({\boldsymbol {x}})={\frac {\sum _{i=1}^{n}x_{i}^{4}-16x_{i}^{2}+5x_{i}}{2}}$	$X=\underbrace {-2.903534,\ldots ,-2.903534} _{(n){\text{ times}}}$ $-39.16617n<f(X)<-39.16616n$	$-5\leq x_{i}\leq 5$, $1\leq i\leq n$.
Simionescu function	$f(x,y)=0.1xy$, ${\text{subjected to: }}x^{2}+y^{2}\leq \left(r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right)^{2}$ ${\text{where: }}r_{T}=1,r_{S}=0.2{\text{ and }}n=8$	$f(\pm 0.85586214,\mp 0.85586214)=-0.072625$	$-1.25\leq x,y\leq 1.25$

Функції для алгоритмів багатокритеріальної оптимізації

Назва / Рисунок	Формула	Мінімум	Область пошуку
Binh and Korn function	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=4x^{2}+4y^{2}\\f_{2}\left(x,y\right)&=\left(x-5\right)^{2}+\left(y-5\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=\left(x-5\right)^{2}+y^{2}\leq 25\\g_{2}\left(x,y\right)&=\left(x-8\right)^{2}+\left(y+3\right)^{2}\geq 7.7\\\end{cases}}$	$0\leq x\leq 5$, $0\leq y\leq 3$
Chakong and Haimes function	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=2+\left(x-2\right)^{2}+\left(y-1\right)^{2}\\f_{2}\left(x,y\right)&=9x-\left(y-1\right)^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=x^{2}+y^{2}\leq 225\\g_{2}\left(x,y\right)&=x-3y+10\leq 0\\\end{cases}}$	$-20\leq x,y\leq 20$
Fonseca and Fleming function	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=1-\exp \left(-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right)\\\end{cases}}$		$-4\leq x_{i}\leq 4$, $1\leq i\leq n$
Test function 4	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x^{2}-y\\f_{2}\left(x,y\right)&=-0.5x-y-1\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=6.5-{\frac {x}{6}}-y\geq 0\\g_{2}\left(x,y\right)&=7.5-0.5x-y\geq 0\\g_{3}\left(x,y\right)&=30-5x-y\geq 0\\\end{cases}}$	$-7\leq x,y\leq 4$
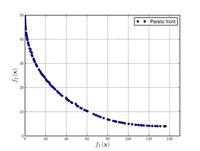
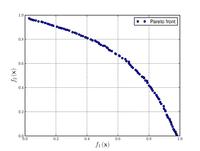
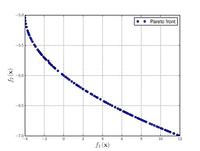
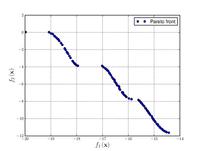
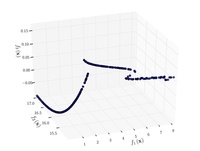
Kursawe function	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}$		$-5\leq x_{i}\leq 5$, $1\leq i\leq 3$.
Schaffer function N. 1	${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)&=x^{2}\\f_{2}\left(x\right)&=\left(x-2\right)^{2}\\\end{cases}}$		$-A\leq x\leq A$. Values of $A$ form $10$ to $10^{5}$ have been used successfully. Higher values of $A$ increase the difficulty of the problem.
Schaffer function N. 2	${\text{Minimize}}={\begin{cases}f_{1}\left(x\right)&={\begin{cases}-x,&{\text{if }}x\leq 1\\x-2,&{\text{if }}1<x\leq 3\\4-x,&{\text{if }}3<x\leq 4\\x-4,&{\text{if }}x>4\\\end{cases}}\\f_{2}\left(x\right)&=\left(x-5\right)^{2}\\\end{cases}}$		$-5\leq x\leq 10$.
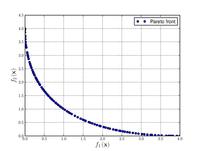
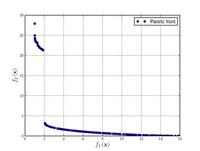
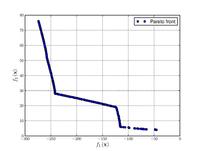
Poloni's two objective function	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)&=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}$ ${\text{where}}={\begin{cases}A_{1}&=0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\A_{2}&=1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\B_{1}\left(x,y\right)&=0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\B_{2}\left(x,y\right)&=1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{cases}}$		$-\pi \leq x,y\leq \pi$
Zitzler–Deb–Thiele's function N. 1	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\\\end{cases}}$		$0\leq x_{i}\leq 1$, $1\leq i\leq 30$.
Zitzler–Deb–Thiele's function N. 2	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$, $1\leq i\leq 30$.
Zitzler–Deb–Thiele's function N. 3	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)\sin \left(10\pi f_{1}\left({\boldsymbol {x}}\right)\right)\end{cases}}$		$0\leq x_{i}\leq 1$, $1\leq i\leq 30$.
Zitzler–Deb–Thiele's function N. 4	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=91+\sum _{i=2}^{10}\left(x_{i}^{2}-10\cos \left(4\pi x_{i}\right)\right)\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\end{cases}}$		$0\leq x_{1}\leq 1$, $-5\leq x_{i}\leq 5$, $2\leq i\leq 10$
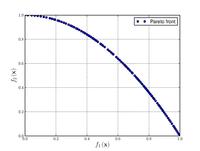
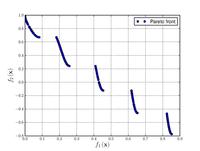
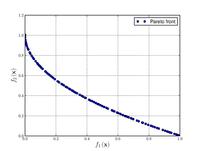
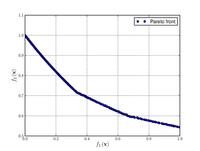
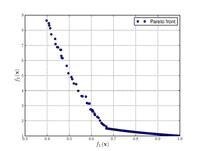
Zitzler–Deb–Thiele's function N. 6	${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}$		$0\leq x_{i}\leq 1$, $1\leq i\leq 10$.
Viennet function	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=0.5\left(x^{2}+y^{2}\right)+\sin \left(x^{2}+y^{2}\right)\\f_{2}\left(x,y\right)&={\frac {\left(3x-2y+4\right)^{2}}{8}}+{\frac {\left(x-y+1\right)^{2}}{27}}+15\\f_{3}\left(x,y\right)&={\frac {1}{x^{2}+y^{2}+1}}-1.1\exp \left(-\left(x^{2}+y^{2}\right)\right)\\\end{cases}}$		$-3\leq x,y\leq 3$.
Osyczka and Kundu function	$F_{1}(x)=-25\left(x_{1}-2\right)^{2}-\left(x_{2}-2\right)^{2}$ $-\left(x_{3}-1\right)^{2}-\left(x_{4}-4\right)^{2}-\left(x_{5}-1\right)^{2}$ ${\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=F_{1}(x)\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{6}x_{i}^{2}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left({\boldsymbol {x}}\right)&=x_{1}+x_{2}-2\geq 0\\g_{2}\left({\boldsymbol {x}}\right)&=6-x_{1}-x_{2}\geq 0\\g_{3}\left({\boldsymbol {x}}\right)&=2-x_{2}+x_{1}\geq 0\\g_{4}\left({\boldsymbol {x}}\right)&=2-x_{1}+3x_{2}\geq 0\\g_{5}\left({\boldsymbol {x}}\right)&=4-\left(x_{3}-3\right)^{2}-x_{4}\geq 0\\g_{6}\left({\boldsymbol {x}}\right)&=\left(x_{5}-3\right)^{2}+x_{6}-4\geq 0\end{cases}}$	$0\leq x_{1},x_{2},x_{6}\leq 10$, $1\leq x_{3},x_{5}\leq 5$, $0\leq x_{4}\leq 6$.
CTP1 function (2 variables)	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x\\f_{2}\left(x,y\right)&=\left(1+y\right)\exp \left(-{\frac {x}{1+y}}\right)\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&={\frac {f_{2}\left(x,y\right)}{0.858\exp \left(-0.541f_{1}\left(x,y\right)\right)}}\geq 1\\g_{1}\left(x,y\right)&={\frac {f_{2}\left(x,y\right)}{0.728\exp \left(-0.295f_{1}\left(x,y\right)\right)}}\geq 1\end{cases}}$	$0\leq x,y\leq 1$.
Constr-Ex problem	${\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=x\\f_{2}\left(x,y\right)&={\frac {1+y}{x}}\\\end{cases}}$	${\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)&=y+9x\geq 6\\g_{1}\left(x,y\right)&=-y+9x\geq 1\\\end{cases}}$	$0.1\leq x\leq 1$, $0\leq y\leq 5$

Посилання

• Optimization Test Problems (англ.)
• 3D Function Grapher (англ.)

Джерела

• Bäck, Thomas. Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. — 1995. p. 328. ISBN 0-19-509971-0.
• Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN 0-471-87339-X.
• Binh T. and Korn U. MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. — 1997. pp. 176—182
• Binh T. A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany. — 1999.