Чотирнадцятикутник

Чотирнадцятикутник

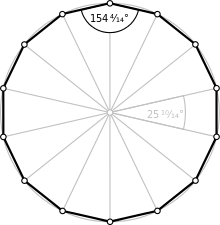
Чотирнадцятикутник - це многокутник з чотирнадцятьма сторонами.

Правильний чотирнадцятикутник

Площа правильного чотирнадцятикутника зі стороною a задається формулою

${\begin{aligned}A&={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}={\frac {14}{4}}a^{2}\left({\frac {{\sqrt {7}}+4{\sqrt {7}}\cos \left({{\frac {2}{3}}\arctan {\frac {\sqrt {3}}{9}}}\right)}{3}}\right)\\&\simeq 15,3345a^{2}\end{aligned}}$

Побудова чотирнадцятикутника

Правильний чотирнадцятикутник не можна побудувати за за допомогою циркуля і лінійки. Однак, його можна побудувати за допомогою методу невсіса, якщо використовувати його разом з трисекцією кута, або з лінійкою з мітками як показано на наведених двох прикладах.

Чотирнадцятикутник в заданому колі:
Анімація (1 хв 47 с) побудови чотирнадцятикутника в колі радіуса ${\overline {OA}}=6$ за допомогою методу невсіса, спираючись на трисекцію кута за допомогою томагавка.

Чотирнадцятикутник з заданою довжиною сторони:
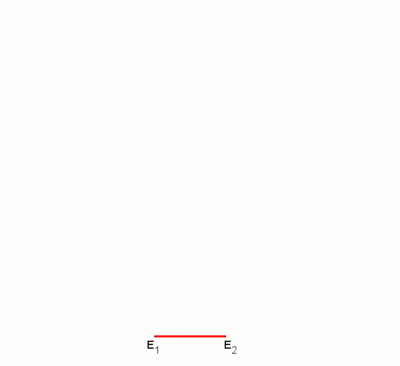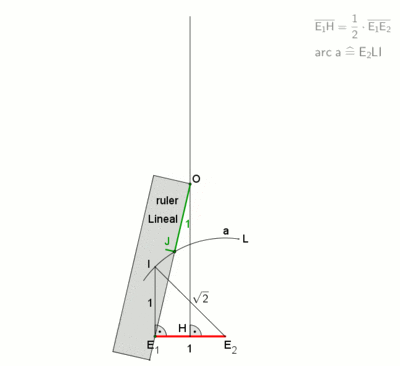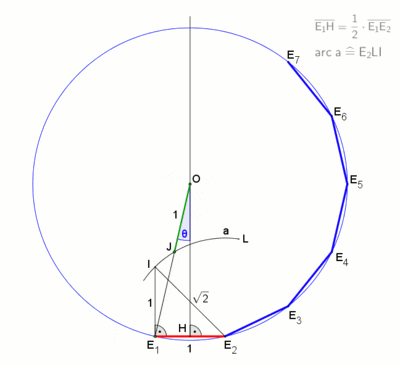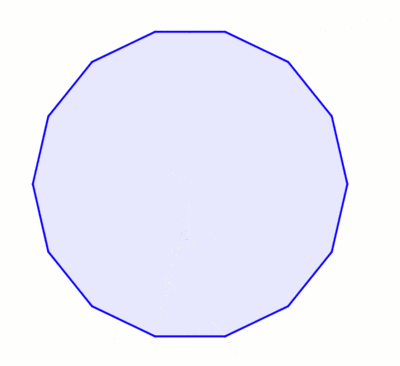
Анімація (1 хв 20 с) побудови за допомогою методу невсіса із застосуванням розміченої лінійки (за Девідом Джонсоном Лейсікцом)

Приблизна побудова чотирнадцятикутника.

Чотирнадцятикутник Петрі

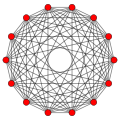
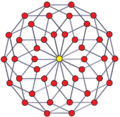
Просторові чотирнадцятикутники існують у вигляді багатокутників Петрі для багатьох багатогранників більш високої розмірності. Приклади наведено в ортогональних проєкціях:

• 
  Гептеракт
• 
  7-ортоплекс
• 
  7-7 дуопірамида
• 
  7-7 дуопризма
• 
  7-7 сімплекс

Література

• Pierre Wantzel.  // Journal de Mathématiques. — 1837.
• Andrew Mattei Gleason. [1] // The American Mathematical Monthly. — 1988.