Зрізання (геометрія)
| Приклади операції «зрізання» | |||
|---|---|---|---|
 Зрізаний квадрат є правильним восьмикутником з двома типами ребер |
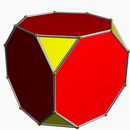 Зрізаний куб |
 Стільник зі зрізаних кубів[en] та октаедрів | |
| Символ Шлефлі | t{4} = {8} | t{4,3} | t{4,3,4} |
| Діаграми Коксетера — Динкіна | |||
У геометрії зріза́ння (або зріза́ння вершин, трунка́ція, англ. truncation) — це операція в просторі будь-якого виміру, унаслідок якої вершини політопа відсікаються, а на місці кожної відсіченої вершини створюється нова фасета.
Термін походить від назв архімедових тіл, що дав їм Кеплер.
Загалом операція «зрізання» застосовується до многогранника (політопа) з певним ступенем свободи щодо вибору глибини зрізання вершини, що можна побачити в статті Нотація Конвея для многогранників[en].

Окремий випадок операції «зрізання«, який зазвичай мається на увазі, є однорідне зрізання, коли оператор зрізання застосовується до правильного многогранника (або правильного політопа), унаслідок чого утворюється однорідний многогранник (однорідний політоп) з рівними довжинами ребер. У цьому разі немає свободи вибору глибини зрізання; вона є однозначною для кожного політопа. Однорідне зрізання вершин многогранника передбачає, що операція «зрізання» проводиться до моменту, коли грані вихідного многогранника стають правильними многокутниками з подвоєним числом сторін.
Загалом усі однорідні політопи з одним кільцевим вузлом (у діаграмі Коксетера — Динкіна) можуть бути однорідно зрізані. Наприклад, ікосододекаедр, який позначається символом Шлефлі як r{5,3} або та діаграмою Коксетера — Динкіна як ![]()
![]()
![]()
![]()
![]() , або
, або ![]()
![]()
![]() має однорідно зрізаний многогранник — зрізаний ікосододекаедр, для якого символ Шлефлі tr{5,3} або та діаграма Коксетера — Динкіна
має однорідно зрізаний многогранник — зрізаний ікосододекаедр, для якого символ Шлефлі tr{5,3} або та діаграма Коксетера — Динкіна ![]()
![]()
![]() .
.
У діаграмі Коксетера — Динкіна результат зрізання вершин проявляється в тому, що всі вузли, суміжні з кільцевим вузлом початкового многогранника, стають також кільцевими вузлами.
Однорідне зрізання правильного трикутного паркету {3,6} утворює правильний шестикутний паркет {6,3}.
Зрізаний n-кутник має 2n сторін (ребер).
Однорідно зрізаний правильний n-кутник є правильним 2n-кутником: t{n} = {2n}.
Повне зрізання[en] (ректифікація) правильного многокутника, r{n}, утворює також правильний многокутник, двоїстий до початкового.
Правильний n-кутник позначається діаграмою Коксетера Динкіна як ![]()
![]()
![]() , а його однорідно зрізаний многокутник — як
, а його однорідно зрізаний многокутник — як ![]()
![]()
![]() . У разі повного зрізання правильного n-кутника отримаємо многокутник
. У разі повного зрізання правильного n-кутника отримаємо многокутник ![]()
![]()
![]() (двоїстий до початкового).
(двоїстий до початкового).
Граф ![]()
![]()
![]() являє собою групу Коксетера I2(n), у якій кожен вузол є дзеркальним, а кожне ребро представляє кут між дзеркалами, а кільця навколо одного чи обох дзеркал показують які з них активні.
являє собою групу Коксетера I2(n), у якій кожен вузол є дзеркальним, а кожне ребро представляє кут між дзеркалами, а кільця навколо одного чи обох дзеркал показують які з них активні.
 {3} {3}
|

|
 t{3} = {6} t{3} = {6}
|

|
 r{3} = {3} r{3} = {3}
|
Зірчасті многокутники також можуть бути зрізані. Зрізана пентаграма {5/2} має вигляд п'ятикутника, але насправді є подвійно-накритим (виродженим) десятикутником ({10/2}) із двома множинами вершин і ребер, що накладені одне на одне.
Зрізана велика гептаграма {7/3} являє собою чотирнадцятикутну зірку (тетрадекаграму) {14/3}.
Під час застосування операції «зрізання» до правильних многогранників Платона або паркетів з правильних многокутників[en] зазвичай використовується однорідне зрізання, що передбачає зрізання вершин до моменту, коли грані вихідного многогранника стають правильними многокутниками з подвоєним числом сторін.

Приклад на малюнку показує послідовний процес зрізання вершин куба до моменту повного зрізання. Кінцевий многогранник — кубооктаедр. Середнє зображення — рівномірно зрізаний куб (напівправильний архімедів многогранник); він має позначення символом Шлефлі t {p,q,...}.

Глибоке зрізання[en] (бітрункація) — це продовження процесу зрізання після повного зрізання[en] вершин, коли всі ребра вихідного многогранника зникають (у процесі зрізання), але залишається внутрішня частина граней вихідного многогранника.
Приклад: зрізаний октаедр є глибоко зрізаним кубом: t{3,4} = 2t{4,3}.
Повне глибоке зрізання, коли процес зрізання продовжується до повного зникнення граней вихідного многогранника (вони стягуються в точку), називається біректифікацією.
Унаслідок операції біректифікації, застосованої до многогранника, утворюється його двоїстий многогранник.
Приклад: октаедр є повним глибоким зрізанням куба (біректифікованим кубом): {3,4} = 2r{4,3}.
Інший тип зрізання, зрізання вершин та ребер[en] (кантеляція), унаслідок якого зрізаються вершини та ребра; водночас на місці зрізаних ребер вихідного многогранника утворюються прямокутники, а на місці зрізаних вершин утворюються нові грані. Повний процес цього зрізання призводить до утворення двоїстого многогранника (чи паркету).

Політопи в просторах з розмірністю вище 3, мають також зрізання фасетів вищої розмірності. Наприклад, операція ранцинація[en] в просторах розмірності вище 3, зрізає вершини, ребра та двовимірні грані політопа; операція стерікація в просторах розмірності вище 4, зрізає вершини, ребра, грані та тривімірні грані (комірки) політопа.
Операція «зрізання ребер» (ско́шування, або зняття́ фа́ски[en]) — подібна до кантеляції , але зберігає оригінальні вершини та замінює ребра на шестикутники.
У 4-вимірному політопі операція «зрізання ребер» замінює ребра на комірки у вигляді подовжених біпірамід.

Альтерна́ція[en] або частко́ве зріза́ння видаляє тільки деякі вершини вихідного многогранника.
Під час застосування цієї операції половина вершин (через одну) вихідного многогранника повністю видаляється. Видаляються також і ребра, що оточують цю вершину. Операція застосовується тільки до многогранників з парною кількістю граней. Після альтернації кількість граней скорочується вдвоє, а квадратні грані вироджуються в ребра.
Приклад: тетраедр є альтернованим кубом, h{4,3}.
Відсікання — більш загальний термін, застосований до многогранників Джонсона, і означає видалення однієї або кількох вершин, ребер, граней многогранника (відсікається у вигляді піраміди або купола), без порушення інших вершин.
Наприклад, тричі відсічений ікосаедр (J63) утворюється з ікосаедра через видалення трьох його вершин разом з ребрами та гранями, що їх оточують (відсікаються три п'ятикутні піраміди).
Інші види часткового зрізання засновані на симетрії, наприклад, як у тетраедрично відсіченому додекаедрі[en]

Процес операції «зрізання» можна узагальнити через надання параметру глибини зрізання від'ємного значення, або провести зрізання таким чином, щоб після перетину середин ребер, вони продовжувалися[уточнити переклад], утворюючи за такої умови схрещені зірчасті многогранники, які можуть бути параметрично пов'язані з правильними зірчастими многокутниками або однорідними зірчастими многогранниками.
Неглибоке зрізання — ребра зменшуються в довжину, кількість ребер у гранях подвоюється, на місці вершин утворюються нові грані.
Однорідне зрізання є окремим випадком неглибокого зрізання, за якого всі новоутворені ребра мають однакову довжину. Під час однорідного зрізання куба його квадратні грані стають правильними восьмикутниками, а на місці вершин утворюються правильні трикутні грані. Отриманий многогранник — зрізаний куб, t{4,3}.
Анти-зрізання. Неглибоке зрізання у зворотному напрямі (назовні від початкової вершини, а не в середину многогранника). У результаті отримаємо многогранник, подібний до вихідного, але з частинами його тілесних кутів, прикріпленими до вершин (замість їх відрізання, як у разі звичайного неглибокого зрізання).
Повне зрізання або ректифікація — граничне неглибоке зрізання, за якого ребра зводяться до точок. Прикладом є кубооктаедр, r{4,3}.
Гіперзрізання. Форма зрізання, яка проходить повз повне зрізання, інвертуючи вихідні ребра, що призводить до появи самоперетинів.
Повне гіперзрізання. Ребра вихідного многогранника повністю інвертуються (перевертаються). Вершини віхідного ребра міняються місцями.
Квазізрізання. Форма зрізання, яка проходить повз повне гіперзрізання, коли перевернуте ребро стає довшим за довжину вихідного ребра. Його можна згенерувати з вихідного многогранника, розглядаючи всі грані як ретроградні, тобто повернуті назад навколо вершини[уточнити переклад]. Наприклад, квазізрізання квадрата дає правильну октаграму (t{4,3}={8/3}), а квазізрізання куба дає однорідний зірчастий зрізаний куб[en], t{4/3,3}.
 ⇨ taC ⇨ taC
|
 Початковий куб Початковий куб
|
 Зрізання Зрізання
⇨ tC |
 Однорідне зрізання Однорідне зрізання
|
 ⇨ tC ⇨ tC
|
 Повне зрізання Повне зрізання
|
 ⇩ thC ⇩ thC
|
 Антизрізання taC Антизрізання taC
|
 Гіперзрізання thC Гіперзрізання thC
| |||||
 ⇧ taC ⇧ taC
|
 Повне квазізрізання Повне квазізрізання
|
 ⇦ ⇦
|
 Квазізрізання Квазізрізання
t{4/3,3} tqC |
 ⇦ tqC ⇦ tqC
|

| |
- Coxeter, H.S.M. Regular Polytopes, (3 видання, 1973), Dover edition, ISBN 0-486-61480-8 (стор. 145–154 Розділ 8: Truncation)
- Norman W. Johnson[en]. Uniform Polytopes, Manuscript (1991)
- Norman W. Johnson[en]. The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Weisstein, Eric W. Truncation(англ.) на сайті Wolfram MathWorld.
- Glossary For Hyperspace
- Polyhedra Names, truncation
| Операції над багатогранниками | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Основа | Зрізання вершин | Розширення (експансія) | Зрізання вершин та ребер[en] (кантеляція) | Омнітрункація[en] (кантітрункація)
Поєднання кантеляції та трункації |
Альтернація[en] , видалення вершин через одну разом з ребрами що її оточують | Зрізання ребер (Фаска[en]) | ||||||
| Зрізання,
Однорідне зрізання (трункація) |
Повне зрізання (ректифікація) | Глибоке зрізання[en] (бітрункація)
Зрізання двоїстого |
Повне глибоке зрізання (біректифікація) | Зрізання вершин через одну (альтернація) | Зрізання носів (снубифікація) | З малою фаскою | З фаскою | |||||
| Альтернація трункації | Альтернація ректифікації | |||||||||||

|

|

|

|

|

|

|

|

|

|

|

|

|
| t0 {p, q}
{p, q} |
t0,1{p, q}
t {p, q} |
t1{p, q}
r{p, q} |
t1,2{p, q}
2t{p, q} |
t2{p, q}
2r{p, q} |
t0,2{p, q}
rr{p, q} |
t0,2{p, q}
rr{p, q} |
t0,1,2{p, q}
tr{p, q} |
ht0{p,q}
h{q, p} |
ht12{p,q}
s{q, p} |
ht012{p,q}
sr{p, q} |
||










