Перейти до вмісту

Китайська математика

Матеріал з Вікіпедії — вільної енциклопедії.

Математика виникла в Китаї в XI столітті до нашої ери[1]. Китайці розробили систему дійсних чисел, яка включає досить великі та від'ємні числа, більше ніж одну систему числення (двійкову та десяткову), алгебру, геометрію, теорію чисел і тригонометрію.

Математика в дев'яти книгах

За часів династії Хань, використовуючи діофантову апроксимацію як чисельний метод, китайці досягли значного прогресу в обчисленні значень многочленів. Такі методи, як метод хибного положення, і такі вирази, як ланцюгові дроби, широко використовувалися і з того часу добре задокументовані. Вони вміли знаходити корінь n-го порядку додатного числа і корені рівнянь[2][3]. Основні тексти того періоду, Математика в дев'яти книгах та Книга про числа та обчислення детально описували процеси розв'язання математичних задач у повсякденному житті[4]. В обох текстах описано, що всі обчислення проводилися за допомогою рахункової дошки, і вони містили обернені елементи, а також ділення з остачею. Тексти містять дії, подібні до методус Гауса та схеми Горнера для лінійної алгебри[5]. Китайська алгебра досягла розквіту в XIII столітті за часів династії Юань, завдяки чому з'явилася тянь-юань-шу.

Внаслідок очевидних мовних і географічних бар’єрів, а також змісту, вважається, що китайська математика і математика стародавнього Середземномор'я розвивалися більш-менш незалежно до того часу, коли Математика в дев'яти книгах досягла своєї остаточної форми, тоді як Книга про числа та обчислення та Хуайнанцзи є приблизно сучасними класичній грецькій математиці. Ймовірно, за часів Древнього Риму певний обмін математичними ідеями відбувався з Азією під час культурних взаємодій. Наприклад, теорема Піфагора описана у трактаті Чжоу бі суань цзін за часів герцога Чжоу. Трикутник Паскаля також був відомий в Китаї за століття до Паскаля[6], наприклад, математику епохи Сун Шень Куо.

Доімперська доба

[ред. | ред. код]
Графічне зображення трикутника (3, 4, 5) у Чжоу бі суань цзін, 500–200 до н. е.
Система числення Oracle Bone script
Лічильний стрижень з позначенням десятків

Династія Шан (1600-1050 рр до н.е.). Однією з найдавніших математичних праць, що збереглися до наших днів, є Книга змін, яка значно вплинула на писемну літературу часів династії Чжоу (1050–256 рр. до н.е.). З математичних знань книга включала складне використання гексаграм. Лейбніц зазначив, що Книга змін (І цзин) містить елементи двійкової системи числення.

Починаючи з періоду Шан, китайці повністю розвинули десяткову систему. З давніх часів китайці розуміли базову арифметику (яка домінувала на Далекому Сході), алгебру, рівняння та від’ємні числа з рахунковими паличками. Хоча китайці були більше зосереджені на арифметиці та більш новітній алгебрі для астрономічних цілей, вони також були першими, хто розробив теорію від’ємних чисел, алгебраїчну геометрію та використання десяткових знаків.

Під час династії Чжоу (1122–256 рр. до н. е.) математика була одним із Шести мистецтв, які учні повинні були опанувати. Для того, щоб бути досконалим поважним чоловіком, порівнянним із поняттям універсальна людина, вимагалося досконало вивчити їх усі. Шість мистецтв сягають корінням у конфуціанство.

Найдавніша робота з геометрії в Китаї походить з філософської школи моїзму (близько 330 р. до н.е.), і була складена послідовниками Мо-цзи (470–390 рр. до н. е.). Мо-цзи описав різні аспекти багатьох галузей, пов’язаних з фізикою, а також надав невелику кількість інформації з математики. Він дав «атомарне» визначення геометричної точки, стверджуючи, що лінія розділена на частини, а частина, яка не має інших частин (тобто не може бути розділена на менші частини), і таким чином утворює крайній кінець лінії, є точкою[7]. Подібно до першого і третього визначення Евкліда та Платона точки як «початку лінії», Мо-цзи стверджував, що «точка може стояти в кінці (лінії) або на її початку... (Щодо її невидимості) нічого схожого на неї немає»[8]. Подібно до атомістів Демокріта, Мо-цзи стверджував, що точка є найменшою одиницею, і її не можна розрізати навпіл, оскільки «ніщо» не може бути розрізано навпіл[8]. Він говорив, що дві лінії однакової довжини завжди закінчуватимуться в одному місці[8], і так вводив визначення для порівняння довжин і паралелей [9] разом із принципами простору та обмеженого простору[10]. Він також описав той факт, що площини без властивості товщини не можуть бути складені в купу, оскільки вони не можуть стикатися одна з одною[11]. У книзі було надано означення кола, діаметра та радіуса, а також визначення об’єму[12].

Історії розвитку математики бракує деяких доказів. Досі ведуться дискусії щодо окремих математичних класиків. Наприклад, Чжоу бі суань цзін датується приблизно 1200–1000 рр. до н.е., проте багато вчених вважали, що трактат був написаний між 300 і 250 рр. до н. е. Чжоу бі суань цзін містить строге доведення теореми Гогу (окремого випадку теореми Піфагора), але більше зосереджується на астрономічних розрахунках. Однак нещодавнє археологічне відкриття бамбукових листків Цінхуа, датованих приблизно 305 р. до н.е. розкрив деякі аспекти математики до династії Цінь, наприклад першу відому десяткову таблицю множення.[13]

Рахівниця була вперше згадана у II ст. до н. е. разом із «рахунком стрижнями» (суан-цзі), коли маленькі бамбукові палички поміщаються в послідовні клітини шахової дошки[14].

Династія Цінь

[ред. | ред. код]

Не так багато відомо про математику династії Цінь або раніше, тому що відбулося спалення книг і поховання вчених приблизно 213–210 рр. до н.е. Знання про цей період можна визначити з цивільних проектів та історичних свідчень. Династія Цінь створила стандартну систему ваг. Цивільні проекти династії Цінь були значними досягненнями людської інженерії. Імператор Цінь Ши Хуан-ді наказав побудувати великі статуї в натуральну величину для палацової гробниці та інших храмів та святинь, а форма гробниці була розроблена з використанням геометричних знань архітектури. Безумовно, одне з найбільших див в історії людства, Великий Китайський мур, вимагало багатьох математичних знань. Усі будівлі та грандіозні проекти епохи Цинь використовували формули обчислення об’єму, площі та пропорції.

Бамбукові гроші Цінь, придбані на антикварному ринку Гонконгу Академією Юелу, за попередніми даними, містять найдавніший зразок математичного трактату.

Династія Хань

[ред. | ред. код]

Під час правління династії Хань числа розглядали в десятковій системі розрядних значень і використовували для обчислень лічильні дошки з набором рахункових паличок, що називається рахування китайськими паличками. На лічильній дошці містилося дев’яти символів і порожнє місце, що представляло нуль[3]. Від’ємні числа та дроби також були включені в розв'язання у великих математичних трактатах того періоду. Математичні трактати того часу, Книга про числа та обчислення та Математика в дев'яти книгах розв'язували основні арифметичні задачі, такі як додавання, віднімання, множення та ділення[4]. Крім того, вони описували методи добування квадратних і кубічних коренів, які згодом застосували для розв’язання квадратних рівнянь та рівнянь третього порядку[5]. В обох трактатах також досягли значного прогресу в лінійній алгебрі, а саме розв’язуванні систем рівнянь із кількома невідомими[15]. Значення числа π в обох текстах прийнято рівним трьом[16]. Проте математики Лю Сінь (пом. 23) і Чжан Хен (78–139) дали точніші наближення числа π, ніж використовували китайці попередніх століть[4]. Математика була інструментом для вирішення практичних завдань того часу, таких як поділ землі або задач, пов'язаних з розподілом платежів[17]. Китайці не зосереджувалися на теоретичних доведеннях, заснованих на геометрії чи алгебрі в сучасному розумінні, доведень формул для знаходження площі чи об’єму. Книга про числа та обчислення і Математика в дев'яти книгах містять численні практичні приклади, які можна використовувати в повсякденному житті[18].

Книга про числа та обчислення

[ред. | ред. код]

Книга про числа та обчислення містить приблизно сім тисяч символів, написаних на 190 бамбукових аркушах[19]. Вона була виявлена разом з іншими письмовими знахідками в 1984 році, коли археологи відкрили гробницю в Чжанцзяшані в провінції Хубей. З документальних свідчень відомо, що ця гробниця була закрита в 186 році до н. е., на початку правління династії Хань[4]. Хоча її зв’язок із Математикою в дев'яти книгах все ще обговорюється вченими, деякі їх частини значно збігаються. Проте текст Suàn shù shū (Книга про числа та обчислення) набагато менш систематичний, ніж Математика в дев'яти розділах, і, складається з кількох більш-менш незалежних коротких розділів тексту, взятих із ряду джерел[19].

Книга про числа та обчислення містить багато алгоритмів розв'язання задач, які будуть використані й у Математиці в дев'яти розділах[19]. Наприклад, в Suàn shù shū квадратний корінь наближено вираховується за допомогою методу хибної позиції, який говорить: «поєднати надлишок і недолік як дільник; (взявши) чисельник недоліку помножити на надлишок знаменника та надлишок чисельника помножте на знаменник дефіциту, об’єднайте їх як дивіденд»[19]. Крім того, у Книзі про числа та обчислення розв’язано системи з двох рівнянь і двох невідомих, використовуючи той самий метод помилкового положення[20].

Математика в дев'яти книгах

[ред. | ред. код]

Математику в дев'яти книгах археологічно датують 179 р. н. е., хоча традиційно датують 1000 р. до н.[21] Хоча автор(и) невідомі, вони зробили великий внесок у розвиток математики східного світу. Задачі складаються із питань, за якими відразу йдуть відповіді та розв'язання[17]. У тексті немає формальних математичних доведень, лише покрокові алгоритми[22]. Лю Хуей надав коментар геометричним та алгебраїчним доведенням задач, що наведені у тексті[3].

Математика в дев'яти книгах була однією з найважливіших з усіх китайських математичних трактатів і складалася з 246 задач[21]. Пізніше її було включено до Десяти обчислювальних канонів, які стали ядром математичної освіти наступних століть[17]. Ця книга містить 246 задач з геодезії, сільського господарства, партнерства, інженерії, оподаткування, розрахунків, розв’язання рівнянь і властивостей прямокутних трикутників[17]. Математика в дев'яти книгах внесла значні вдосконалила розв’язання квадратних рівнянь подібно до схеми Горнера[5]. Вона також значно поглибила відомості у fangcheng ― те, що зараз відомо як лінійна алгебра[20]. У сьомому розділі розв’язується система лінійних рівнянь із двома невідомими за допомогою методу хибного положення, схожого на метод з Книги про числа та обчислення[20]. Розділ восьмий стосується розв’язування лінійних рівнянь з використанням додатних і від’ємних чисел, причому одна задача стосується розв’язання чотирьох рівнянь із п’ятьма невідомими[20]. Математика в дев'яти книгах містить розв'язання системи рівнянь за допомогою методів, подібних до сучасного методу Гаусса та трикутної матриці[20].

Версія Математики в дев'яти книгах, яка послужила основою для сучасних перекладів, була результатом зусиль вченого Дай Чжень. Переписуючи задачі безпосередньо з Енциклопедії Юнле, він поступово перейшов до редагування оригінального тексту разом із включенням власних приміток, що пояснюють його міркування щодо змін[23]. Його робота була вперше опублікована в 1774 році, проте в 1776 році була перевидана, щоб виправити різні помилки, а також включити версію Математики в дев'яти книгах з Південної пісні, яка містила коментарі Лю Хуея та Лі Чуньфена. Остаточна версія роботи Дай Чжень з’явилася в 1777 році під назвою Ripple Pavilion, і ця остаточна версія була широко розповсюджена та стала стандартом для сучасних версій Математики в дев'яти книгах[24]. Однак ця версія піддалася пильній перевірці Го Шученя, який заявив, що відредагована версія все ще містить численні помилки та що не всі оригінальні поправки були внесені самим Дай Чженем[23].

Обчислення числа π

[ред. | ред. код]

У задачах Математики в дев'яти книгах число π=3 при обчисленні завдань, пов’язаних із колами та сферами, наприклад площею поверхні сфери[21]. У тексті немає формули для обчислення числа π, яке дорівнює трьом, але це значення використовується в усіх задачах як Математики в дев'яти книгах, так і Записів майстра, які були створені в той самий період часу[16]. Історики вважають, що це значення числа π було обчислено з використанням співвідношення 3:1 між довжиною кола та його діаметром[21]. Деякі ханьські математики намагалися уточнити це число, наприклад Лю Сінь, який, як вважають, оцінив число π як 3,154[4]. Пізніше Лю Хуей спробував покращити обчислення та оцінив число π до 3,141024. Лю розрахував це значення, використовуючи багатокутники, вписані у шестикутник як нижнє наближення кола[25]. Пізніше Цзу Чонджі виявив, що π обмежене числами 3,1415926 < π < 3,1415927, використавши багатокутники з 24 576 сторонами. Цей розрахунок був відкритий в Європі в XVI столітті[26].

Немає чіткого методу або запису про те, як він розрахував цю оцінку[4].

Ділення та дії з коренями

[ред. | ред. код]

Основні арифметичні дії (додавання, віднімання, множення та ділення) виконували ще до династії Хань[4]. У Математиці в дев'яти книгах вони розглянуті як належне і просто інструктують читача їх виконувати[20]. Ханьські математики обчислювали квадратні та кубічні корені подібно до ділення, а задачі з діленням і обчисленням кореня зустрічаються в четвертому розділі Математики в дев'яти книгах[27]. Обчислення квадратних і кубічних коренів із чисел виконується шляхом послідовного наближення, так само як ділення, і часто використовує схожі терміни, такі як ділене (shi) і дільник (fa) протягом усього обчислення[5]. Пізніше процес послідовного наближення було розширено до розв'язування систем другого та третього порядку, таких як , використовуючи метод, подібний до схеми Горнера[5]. Під час правління династії Хань метод не був поширений для розв’язування рівнянь та систем n-го порядку, однак цей метод пізніше був використаний для їх розв'язання[5].

Fangcheng (основи лінійної алгебри) на рахунковій дошці

Лінійна алгебра

[ред. | ред. код]

Книга про числа та обчислення — перший відомий текст, у якому розв’язуються системи рівнянь із двома невідомими[20]. Всього Книга про числа та обчислення містить три типи задач, пов’язаних із розв’язуванням систем рівнянь за допомогою методу хибного положення, які описані практичними термінами[20]. У VII розділі Математики в дев'яти книгах також розглядається розв’язування системи двох рівнянь із двома невідомими методом хибного положення[20]. Щоб знайти більше з двох невідомих, метод хибного положення дає вказівку читачеві помножити менші члени zi на більші члени mu[20]. Щоб знайти менше з двох невідомих, просто додайте менші члени[20].

У розділі VIII Математики в дев'яти книгах описано алгоритми розв’язування рівнянь із різною кількістю невідомих[20]. У цьому розділі цей процес називається fangcheng[20]. Багато істориків вирішили залишити термін fangcheng без перекладу через суперечливі докази того, що означає цей термін. Сьогодні багато істориків під цим словом розуміють лінійну алгебру. У цьому розділі метод додавання Гаусса та метод заміни використовуються для розв’язування систем рівнянь із багатьма невідомими[20]. Завдання виконувалися на обчислювальній дошці та включали використання від’ємних чисел, а також дробів[20]. Обчислювальна дошка була фактично матрицею, де у верхньому рядку вказане значення першої змінної рівняння, а у нижньому – другої[20].

Коментар Лю Хуея до Математики в дев'яти розділах

[ред. | ред. код]
Метод Лю Хуея

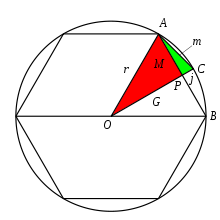
Коментар Лю Хуея до Математики в дев'яти книгах є найпершим доступним виданням оригінального тексту[21]. Більшість вважає, що Хуей був математиком у часи зразу після династії Хань. У своєму коментарі Хуей сформулював і довів деякі твердження з алгебраїчного або геометричного погляду[18]. Наприклад, у Математиці в дев'яти книгах значення π приймається рівним 3 у задачах про кола чи сфери[16]. У своєму коментарі Лю Хуей знаходить точнішу оцінку числа π за допомогою методу вичерпування[16]. Цей метод передбачає створення послідовних багатокутників, вписаних у коло, щоб зрештою площа кожного наступного багатокутника прямувала до площі круга[16]. На основі цього методу Лю Хуей стверджував, що значення π становить приблизно 3,14[4]. Лю Хуей також представив геометричне доведення добування квадратного та кубічного кореня, подібне до грецького методу, який передбачав розрізання квадрата чи куба на будь-якій лінії або ділянці та визначення кореня через симетрію решти прямокутників[27].

Три королівства, Джин і Шістнадцять королівств

[ред. | ред. код]
Огляд морського острова, Лю Хуей
Алгоритм Сунь-цзи для ділення, 400 р. до н. е.
Ділення методом аль-Хорезмі, IX ст.
Пам'ятник Цзу Чунчжи.

У III столітті Лю Хуей написав свій коментар до Математики в дев'яти книгах, а також написав трактат Хайдао Суаньцзін, в якому йдеться про використання теореми Піфагора (вже відомої з Математики в дев'яти книгах) і трикутну, чотирикутну тріангуляцію для геодезії; його досягнення в математичних дослідженнях на тисячоліття випередили досягнення на Заході[28]. Він був першим китайським математиком, який обчислив π =3,1416 за допомогою свого алгоритму. Він відкрив принцип Кавальєрі, який використав для знаходження формули об’єму циліндра, а також розробив основи диференціального та інтегрального числення у III ст. н. е.

Інтерполяція дробів для числа π

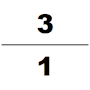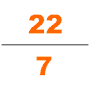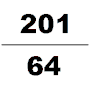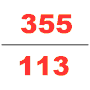
У IV ст. інший математик Цзу Чунчжі створив Да Мін Лі. Цей календар був спеціально розрахований для передбачення багатьох космологічних циклів, які відбуватимуться в певний період часу. Про життя Цзу Чунчжі насправді відомо дуже мало. Єдині джерела знаходяться в Книзі Суй. Відомо, що Цзу Чунчжі належав до династії математиків. Він використав алгоритм Лю Хуея для обчислення числа π, застосований до 12288-кутника, і отримав значення π з точністю до 7 знаків після коми (між 3,1415926 і 3,1415927), яке залишалося найточнішим наближенням π на наступні 900 років. Він також застосував інтерполяцію Хе Чентяня для наближення ірраціонального числа дробом у своїх астрономічних і математичних роботах, він отримав як наближене значення числа π; Йошіо Мікамі зазначив, що ані греки, ані індуси, ані араби не знали про цю дробову апроксимацію до π, аж доки голландський математик Адріан Антонісзум не відкрив її заново в 1585 році, «отже, китайці володіли цим найбільш надзвичайним з усіх дробових значень на ціле тисячоліття раніше, ніж Європа»[29].

Разом зі своїм сином Цзу Геном Цзу Чунчжі застосував принцип Кавальєрі, щоб обчислити об’єму кулі. Окрім формул для об’єму кулі, його книга також містила формули кубічних рівнянь і точне значення числа π. Його праця Чжуй Шу була виключена з програми математики під час династії Сун і втрачена. Багато хто вважав, що Чжуй Шу містить формули та методи для лінійної, матричної алгебри, алгоритм для обчислення значення π, формулу для об’єму кулі. Текст також міг містити астрономічні методи інтерполяції зі знаннями, подібними до сучасної математики.

Математичний посібник під назвою Математична класика Сунь-цзи, датований між 200 і 400 рр. до н.е., містив найдетальніший покроковий опис алгоритму множення та ділення з рахувальними паличками. Загадковим є те, як Сунь-цзі міг вплинути на розвиток позиційних систем числення та алгоритми ділення на Заході. Європейські джерела навчилися цих методів в XIII столітті з латинського перекладу праці Аль-Хорезмі початку IX століття. Метод ділення Аль-Хорезмі майже ідентичний алгоритму рахування китайськими паличками Сунь-цзи, навіть щодо стилістичних питань (наприклад, використання пробілів для представлення кінцевих нулів). Подібність припускає, що результати, можливо, не були незалежним відкриттям. Ісламські коментатори роботи Аль-Хорезмі вважали, що вона насамперед узагальнює індуїстські знання. Відмова Аль-Хорезмі посилатися на свої джерела ускладнює визначення того, чи ці джерела, своєю чергою, дізналися про процедуру з Китаю[30].

У V столітті в посібнику Чжан Цюцзянь суанцзин розглядалися лінійні та квадратні рівняння. До цього часу китайці вже мали поняття про від'ємні числа.

Династія Тан

[ред. | ред. код]

За часів династії Тан вивчення математики було досить стандартним у великих школах. Десять обчислювальних канонів — збірка з десяти китайських математичних робіт, складених математиком ранньої династії Тан Лі Чуньфеном (李淳風 602–670), були офіційними математичними текстами для імперських іспитів з математики. Династії Суй і Тан керували Школою обчислень[31].

Ван Сяотун був великим математиком часів династії Тан, він написав книгу Продовження стародавньої математики, у якій вперше з'являються загальні алгоритми розв'язання кубічних рівнянь[32].

Таблиця синусів індійського математика Аріабгати була перекладена в китайський математичний трактат Кайюань Чжаньцзін, написаний у 718 році, за часів династії Тан[33]. Хоча китайці досягли успіху в інших галузях математики, таких як геометрія твердого тіла, біномНьютона та складні алгебраїчні формули, ранні форми тригонометрії не були настільки широко поширені, як у сучасній їм індійській та ісламській математиці[34].

І Сіну, математику та буддійському ченцю, приписують створення таблиці тангенсів. Натомість китайці використовували емпіричний замінник, відомий як чонг ча, тоді як було відоме практичне використання плоскої тригонометрії з використанням синуса, тангенса та секанса[34]. І Сін був відомий своєю геніальністю, і, як відомо, він обчислив кількість можливих позицій у настільній грі го (хоча без символу нуля йому було важко вказати число).

Династії Сун і Юань

[ред. | ред. код]

Математик династії Сун Цзя Сян розробив адитивний мультиплікативний метод добування квадратного та кубічного кореня, у якому реалізував схему Горнера[35].

Трикутник Ян Хуей (трикутник Паскаля) з використанням паличкових чисел, зображення з трактату Чжу Шицзе, 1303 рік

Чотири видатні математики жили у часи династій Сун і Юань, зокрема у XII і XIII століттях: Ян Хуей, Цінь Цзюшао, Лі Е (Лі Чжі) і Чжу Шицзе. Ян Хуей, Цінь Цзюшао, Чжу Шицзе використовували метод Горнера - Руффіні 600 років тому для розв'язання певних типів лінійних, квадратних, кубічних і четвертого степеня рівнянь, обчислення коренів. Ян Хуей також був першою людиною в історії, яка винайшла трикутник Паскаля разом із його біноміальним доведенням (хоча найдавніша згадка про трикутник Паскаля в Китаї існує ще до XI ст. н. е.). Лі Е, з іншого боку, досліджував форму алгебраїчної геометрії, засновану на tiān yuán shù. Його книга Ceyuan haijing революціонізувала ідею вписування кола в трикутники, перетворивши цю проблему геометрії на алгебру замість традиційного методу використання теореми Піфагора. Го Шоуцзін, математик цього ж часу, також працював у галузі сферичної тригонометрії з метою вдосконалення астрономічних обчислень. На цьому етапі математичної історії багато з сучасної західної математики вже було відкрито китайськими математиками. На деякий час розвиток математики у Китаї сповільнився, аж до епохи Відродження китайської математики в XIII столітті. Тоді китайські математики розв’язували рівняння методами, яких Європа не знала аж до XVIII століття. Найбільшими досягненнями цієї епохи вважають дві книги Чжу Шицзе Суаньсю цімен і Нефритове дзеркало чотирьох невідомих. Зокрема, він розробив метод, еквівалентний центральній конденсації Гаусса.

Цінь Цзюшао (бл. 1202 – 1261) був першим, хто ввів символ нуля в китайську математику[36]. До цього нововведення замість нулів у системі рахункових паличок використовувалися пробіли[37]. Одним із найважливіших внесків Цінь Цзюшао був його метод розв’язування рівнянь вищих порядків. Про на розв’язок Цінь рівняння 4-го порядку Йошіо Мікамі сказав: "Хто може заперечувати той факт, що відома схема Горнера використовувалася в Китаї майже на шість століть раніше, ніж у Європі?"[38] Цинь також розв'язав рівняння 10-го порядку[39].

Трикутник Паскаля вперше проілюстрував у Китаї Ян Хуей у своїй книзі Сянцзе Цзючжан Суанфа (詳解九章算法), хоча він був описаний раніше, приблизно в 1100 році Цзя Сянем[40]. Хоча Вступ до обчислень (算學啓蒙), написаний Чжу Шицзе у 1299 році, не містив нічого нового в китайській алгебрі, він мав великий вплив на розвиток японської математики[41].

Алгебра

[ред. | ред. код]

Морське дзеркало вимірювань кола

[ред. | ред. код]
Магічні концентричні кола Ян Хуея – сума чисел на кожному колі та діаметрі (без урахування середини 9) дорівнює 138

Ceyuan haijing (кит. 測圓海鏡), або Морське дзеркало вимірювань кола, — це збірка із 692 формул і 170 задач, пов’язаних із вписаним у трикутник колом, написана Лі Е (або Лі Чжі) (1192–1272 рр. н. е.). Він використовував тянь юань шу, щоб перетворити складні геометричні задачі на алгебраїчні. Потім він використав fan fa, або схему Горнера, для розв’язування рівнянь до шостого степеня, хоча він не описав свій метод розв’язування рівнянь[42]. Лі Е жив у Пекіні, одного разу Хублай-хан запропонував йому посаду в уряді в 1206 році, але він ввічливо знайшов привід відмовитися. Його Морське дзеркало вимірювань кола включає 170 задач, що стосуються деяких задач, що зводяться до поліноміальних рівнянь шостого степеня. Хоча він не описав свій метод розв’язування рівнянь, здається, що він не сильно відрізнявся від того, який використовували Чу Ши-цзе та Горнер. Іншими, хто використовував метод Горнера, були Цінь Чіу-шао (бл. 1202 – бл. 1261) і Ян Хуей (бл. 1261–1275).

Нефритове дзеркало чотирьох невідомих

[ред. | ред. код]
Факсимільне зображення з Нефритового дзеркала чотирьох невідомих

Нефритове дзеркало чотирьох невідомих було написане Чжу Шицзе в 1303 році й знаменує вершину в розвитку китайської алгебри. Чотири елементи, які називаються небом, землею, людиною та матерією, представляли чотири невідомі величини в його алгебраїчних рівняннях. Автор має справу з рівносильними рівняннями та рівняннями до чотирнадцятого степеня. Для розв’язання цих рівнянь автор використовує метод fan fa, який сьогодні називають схемою Горнера[43].

Існує багато формул із сумами числових рядів, поданих без доведення у Дзеркалі. Кілька рядів:[44]

Математичний трактат у дев'яти розділах

[ред. | ред. код]

Математичний трактат у дев’яти розділах (не плутайте з Математикою в дев'яти книгах) був написаний багатим губернатором і міністром Цінь Чзюшао (прибл. 1202 – прибл. 1261) і з винаходом методу конгруенцій знаменує вершину китайського аналізу[42].

Магічні квадрати та магічні кола

[ред. | ред. код]

Найдавніші відомі магічні квадрати порядку понад три приписують Яну Хуею (бл. 1261–1275), який працював з магічними квадратами порядків понад 10[45]. Серед його внесків, які дійшли до наших днів, є найдавніші китайські магічні квадрати порядку понад три, включаючи два кожен порядків з четвертого по восьмий і по одному з порядків дев'ятого і десятого. Він також працював з магічним колом.

Тригонометрія

[ред. | ред. код]

Зародковий стан тригонометрії в Китаї повільно почав змінюватися під час правління династії Сун (960–1279), коли китайські математики звернули увагу на потреби сферичної тригонометрії в календарній науці та астрономічних розрахунках[34]. Ерудит і чиновник Шень Куо (1031–1095) використовував тригонометричні функції для розв'язання математичних задач хорд і дуг[34]. Джозеф В. Даубен зазначає, що у формулі Шеня кіл, що перетинаються, обчислюється наближене значення дуги кола s як s = c + 2 v 2 / d, де d — діаметр, v — версус, c — довжина хорди c, що стягує дугу[46]. Сал Рестіво пише, що робота Шеня щодо довжин дуг кіл забезпечила основу для сферичної тригонометрії, розробленої в XIII ст. математиком і астрономом Ґо Шоуцзіном (1231–1316)[47]. Гоше та Нідем стверджують, що Ґо використовував сферичну тригонометрію у своїх розрахунках для вдосконалення китайського календаря та астрономічних обрахунках[34][48]. Разом із пізнішою китайською ілюстрацією математичних доказів Ґо XVII століття Нідхем пише:

Го використовував чотирикутну сферичну піраміду, основний чотирикутник якої складався з однієї екваторіальної та однієї екліптичної дуг разом із двома меридіанами, один з яких проходив через літнє сонцестояння... Таким чином, зміг отримати du lü (градуси екватора, що відповідають градусам екліптики), ji cha (значення хорд для заданих дуг екліптики), і cha lü (різниця між хордами дуг, що відрізняються на 1 градус).[49]

Попри досягнення роботи Шеня і Ґо в тригонометрії, ні одна значна праця з китайської тригонометрії не була опублікована до 1607 року, в той же час Начала Евкліда публікувалися двічі китайським чиновником і астрономом Сюй Ґуанці (1562–1633) та італійським єзуїтом Маттео Річчі (1552–1610)[50].

Династія Мін

[ред. | ред. код]

Після повалення династії Юань Китай став підозріло ставитися до монгольського впливу. Суд відмовився від математики та фізики на користь ботаніки та фармакології. Державні іспити включали мало математики, і те небагато, що вони включали, ігнорувало останні розробки. Марцлофф пише:

Наприкінці XVI століття китайська автохтонна математика, яку знали самі китайці, не складала майже нічого, лише обчислення на абаку, тоді як у XVII та XVIII століттях ніщо не можна було порівняти з революційним прогресом на театрі європейської науки. Більше того, у той самий період ніхто не міг повідомити, що відбувалося в більш віддаленому минулому, оскільки самі китайці мали про це лише уривчасті знання. Не слід забувати, що в самому Китаї автохтонна математика не була заново відкрита у великому масштабі до останньої чверті XVIII століття.[51]

Відповідно менше уваги вчені приділяли математиці. Видатні математики, такі як Гу Інсян і Тан Шуньчжи, здається, не знали методу збільшення множення[52]. Без усних співрозмовників, які б пояснювали їх, тексти швидко ставали незрозумілими; що ще гірше, більшість задач можна розв'язати більш елементарними методами. Тоді для середнього вченого тянь-юань здавався нумерологією. Коли У Цзін об’єднав усі математичні праці попередніх династій в Анотації обчислень у дев’яти розділах про математичне мистецтво, він опустив тянь -юань-шу та метод збільшення множення[53].

Рахівниця (абак)

Натомість математичний прогрес зосередився на обчислювальних інструментах. У XV столітті абак отримав форму suan pan. Простий у використанні та носінні, швидкий і точний, він витіснив паличкові обчислення як переважну форму обчислень. Чжусуань, арифметичні розрахунки за допомогою рахівниці, надихнули на численні нові роботи. Suanfa Tongzong (Загальне джерело обчислювальних методів), XVII-томна праця, опублікована в 1592 році Ченом Давеєм, використовувалася понад 300 років. Чжу Цзайюй використовував рахівницю з 81 позицією для обчислення квадратного кореня та кубічного кореня з точністю від 2 до 25 цифр, точність, яка дозволила йому розробити рівномірно-темперований стрій.

Наприкінці XVI століття Маттео Річчі вирішив опублікувати західні наукові праці, щоб отримати посаду при Імператорському дворі. За сприяння Сюя Ґуанці він зміг перекласти Початки Евкліда, використовуючи ті ж методи, що використовуються для викладання класичних буддійських текстів[54]. Інші місіонери наслідували його приклад, перекладаючи західні праці про спеціальні функції (тригонометрію та логарифми), якими нехтували в китайській традиції[55]. Однак тогочасні вчені вважали акцент на доведеннях — на відміну від розв’язаних задач — незрозумілим, і більшість із них продовжували працювати лише на класичних текстах[56].

Династія Цзин

[ред. | ред. код]

За правління імператора Сюаньє, який навчився західній математиці від єзуїтів і був відкритий до зовнішніх знань та ідей, китайська математика мала короткий період офіційної підтримки[57]. За вказівкою Сюаньє Мей Гоучен і троє інших видатних математиків склали LIII-томну працю під назвою Шулі Цзін'юнь (Суть математичних досліджень), яка була надрукована в 1723 році та містила систематичний вступ до західних математичних знань[58]. В той самий час Мей Гоучен також написав Мейші Коншу Цзянь (Збірка творів Мея). Мейші Коншу Цзянь був енциклопедичним підсумком майже всіх шкіл китайської математики того часу, але він також включав міжкультурні роботи Мея Уендіня (1633–1721), діда Гоученга[59][60]. Збірка мала на меті полегшити труднощі для китайських математиків, які працюють над західною математикою, у відстеженні цитувань[61].

У 1773 році імператор Хунлі вирішив скласти Повну бібліотеку чотирьох скарбниць (або Сику цюаньшу). Дай Чжень (1724–1777) вибрав і відредагував Математику в дев'яти книгах з Енциклопедії Юнле та кілька інших математичних праць династій Хань і Тан[62]. Давно зниклі математичні роботи династій Сун і Юань, такі як Si-yüan yü-jian і Ceyuan haijing, також були знайдені та надруковані, що безпосередньо призвело до хвилі нових досліджень[63]. Найбільш коментованими роботами були Jiuzhang suanshu xicaotushuo (Ілюстрації процесу обчислення до Математики в дев'яти книгах), надані Лі Хуаном, і Si-yüan yü-jian xicao (Докладне пояснення Si-yüan yü-jian) Луо Шиліня[64].

Західні впливи

[ред. | ред. код]

У 1840 році Перша опіумна війна змусила Китай відкрити свої двері та поглянути на зовнішній світ, що також призвело до напливу західних математичних досліджень. У 1852 році китайський математик Лі Шанлань і британський місіонер Олександр Вайлі спільно переклали наступні IX томів Елементів і XIII томів Алгебри[65][66]. За сприяння Джозефа Едкінса незабаром з'явилися нові роботи з астрономії та обчислень. Китайські вчені спочатку не були впевнені, як варто підходити до нових робіт: чи вивчення західних знань не є формою підпорядкування іноземним загарбникам? Але наприкінці століття стало зрозуміло, що Китай може розпочати відновлення свого суверенітету лише шляхом інкорпорації західних підходів. Китайські вчені, яких навчали в західних місіонерських школах із (перекладених) західних текстів, швидко втратили зв’язок з місцевою традицією. Ті, хто навчався самостійно або був у традиціоналістських колах, однак, продовжували працювати в традиційних рамках алгоритмічної математики, не вдаючись до західної символіки[67]. Проте, як зазначає Марцлофф, «з 1911 року в Китаї практикувалася виключно західна математика»[68].

У сучасному Китаї

[ред. | ред. код]

Китайська математика пережила значне відродження після створення сучасної Китайської республіки в 1912 році. З того часу сучасні китайські математики досягли численних досягнень у різних математичних галузях.

Деякі відомі сучасні етнічні китайські математики:

  • Шіінг-Шен Черн вважався лідером у галузі геометрії та одним із найвидатніших математиків XX-го століття, був нагороджений премією Вольфа за внесок у математику[69][70].
  • Кай Фан зробив внесок у теорію фіксованої точки, а також вплинув на нелінійний функціональний аналіз, який знайшов широке застосування в математичній економіці та теорії ігор, теорії потенціалу, варіаційному численні та диференціальних рівняннях.
  • Шинтан Яу, лауреат медалі Філдса, вплинув як на фізику, так і на математику, і він активно працював на стику геометрії з теоретичною фізикою і згодом був нагороджений за свій внесок.
  • Теренс Тао, лауреат медалі Філдса та вундеркінд китайського походження, був наймолодшим учасником в історії Міжнародної математичної олімпіади у віці 10 років, вигравши бронзову, срібну та золоту медалі. Він залишається наймолодшим володарем кожної з трьох медалей в історії Олімпіади.
  • Їтан Чжан, теоретик чисел, який встановив першу кінцеву межу проміжків між простими числами.
  • Чень Цзінжунь, теоретик чисел, який довів, що кожне досить велике парне число можна записати як суму або двох простих чисел, або простого та напівпростого числа, що зараз називається теоремою Ченя[71]. Його робота була важливою для дослідження гіпотези Ґольдбаха.

Китайська Народна Республіка

[ред. | ред. код]

У 1949 році, на початку утворення Китайської Народної Республіки, уряд приділяв велику увагу справі науки, хоча країна перебувала в скрутному становищі через брак коштів. Китайська академія наук була заснована в листопаді 1949 року, Інститут математики — у липні 1952 року. За 18 років після 1949 року кількість опублікованих статей у три рази перевищувала загальну кількість статей до 1949 року. Багато з них не тільки заповнили прогалини в минулому Китаю, але й досягли передового світового рівня[72].

Під час хаосу Культурної революції науки занепали. Проте математики Чень Цзінжунь, Хуа Луоген, Чжан Гуанхоу та інші намагаються продовжити свою роботу. З публікацією літературної праці Го Можо «Наукова весна» китайські науки та математика пережили відродження. У 1977 р. в Пекіні було сформульовано новий план розвитку математики, відновлено роботу математичного товариства, зміцнено математичну освіту та фундаментальні теоретичні дослідження[72].

Важливим досягненням китайської математики є те, як Ся Чжихон довів гіпотезу Пенлеве в 1988 році. Гіпотеза Пенлеве — важлива гіпотеза в галузі енергетичних систем, запропонована в 1895 році. Дуже важливою нещодавньою подією для проблеми 4-х тіл є те, що Сюе Цзіньсінь і Долгопят довели сингулярність без зіткнень у спрощеній версії системи 4-х тіл приблизно у 2013 році[73].

Крім того, у 2007 році Шень Вейсяо та Козловський, Ван-Стрієн довели дійсну гіпотезу Фату: дійсні гіперболічні многочлени щільні в просторі дійсних многочленів зі сталим степенем. Цю гіпотезу вперше сформував Фату в 1920-х роках, а пізніше Смейл висунув її в 1960-х роках. Доказ гіпотези Фату є одним із найважливіших досягнень у конформній динаміці за останнє десятиліття[73].

Міжнародна математична олімпіада

[ред. | ред. код]

Порівняно з іншими країнами-учасницями Міжнародної математичної олімпіади, Китай має найвищі командні результати та найбільшу кількість разів золоту медаль МMO вигравали представники Китаю[74].

Освіта

[ред. | ред. код]

Перша згадка про книгу, яка використовується для вивчення математики в Китаї, датована II ст. н. е. (Хоу Ханьшу: 24, 862; 35, 1207 сувої). Вказано, що Ма Сюй, що навчався близько 110 року, і Чжен Сюань (127–200) вивчали Математику в девя'ти книгах. Крістофер Каллен стверджує, що математику, подібно до медицини, викладали усно. Стилістика Suàn shù shū з Чжанцзяшаня свідчить про те, що текст був зібраний з різних джерел, а потім зазнав кодифікації[75].

Див. також

[ред. | ред. код]

Примітки

[ред. | ред. код]
  1. ↑ Chinese overview
  2. ↑ Needham, 1959, с. 65—66.
  3. ↑ а б в East Asian mathematics в онлайн-версії «Encyclopædia Britannica». Karine Chemla (англ.)
  4. ↑ а б в г д е ж и Needham, 1959.
  5. ↑ а б в г д е Needham, 1955.
  6. ↑ Swetz, Frank J.; Kao, T. I. (1988). Was Pythagoras Chinese? an examination of right triangle theory in ancient China. University Park, Pa: Pennsylvania State University Press. ISBN 978-0-271-01238-4.
  7. ↑ Needham, 1959, с. 91.
  8. ↑ а б в Needham, 1959, с. 92.
  9. ↑ Needham, 1959, с. 92—93.
  10. ↑ Needham, 1959, с. 93.
  11. ↑ Needham, 1959, с. 93—94.
  12. ↑ Needham, 1959, с. 94.
  13. ↑ Qiu, Jane (7 січня 2014). Ancient times table hidden in Chinese bamboo strips. Nature (англ.). doi:10.1038/nature.2014.14482. ISSN 0028-0836. Процитовано 17 листопада 2023.
  14. ↑ Ifrah, Georges (2001). The universal history of computing: from the abacus to the quantum computer. New York: Wiley. ISBN 978-0-471-39671-0.
  15. ↑ Hart, 2011.
  16. ↑ а б в г д Lennart, Bergren (1997). Pi: A Source Book. New York. ISBN 978-1-4757-2738-8.
  17. ↑ а б в г Yong, Lam Lay (1994). Jiu zhang suanshu (nine chapters on the mathematical art): An overview. Archive for History of Exact Sciences (англ.). 47 (1): 1—51. doi:10.1007/BF01881700. ISSN 0003-9519. JSTOR 41133972.
  18. ↑ а б Siu, 1993.
  19. ↑ а б в г Dauben, 2008.
  20. ↑ а б в г д е ж и к л м н п р с т Hart, 2011, с. 11—85.
  21. ↑ а б в г д Dauben, 2013.
  22. ↑ Straffin, Philip D. (1 червня 1998). Liu Hui and the First Golden Age of Chinese Mathematics. Mathematics Magazine (англ.). 71 (3): 163—181. doi:10.2307/2691200. JSTOR 2691200.
  23. ↑ а б Hart, 2011, с. 32—33.
  24. ↑ Dauben, 2013, с. 211—216.
  25. ↑ Hart, 2011, с. 39.
  26. ↑ Wilson, Robin (2013). Early Chinese Mathematics. The Mathematical Intelligencer (англ.). 35 (2): 80. doi:10.1007/s00283-013-9364-x. ISSN 0343-6993.
  27. ↑ а б Yong, Lam Lay (1970). The Geometrical Basis of the Ancient Chinese Square-Root Method. Isis (англ.). 61 (1): 92—102. doi:10.1086/350581. ISSN 0021-1753. JSTOR 229151.
  28. ↑ Swetz, Frank J.; Liu, Hui (1992). The sea island mathematical manual: surveying and mathematics in ancient China. University Park, Pa: Pennsylvania State University Press. с. 63. ISBN 978-0-271-00795-3. Процитовано 18 листопада 2023.
  29. ↑ Mikami, 1913, с. 50.
  30. ↑ Lam Lay Yong (1996). The Development of Hindu Arabic and Traditional Chinese Arithmetic (PDF). Chinese Science. 13: 35—54. Архів оригіналу (PDF) за 21 березня 2012. Процитовано 31 грудня 2015.
  31. ↑ Karp, Alexander; Schubring, Gert (2014). Handbook on the history of mathematics education. New York: Springer. с. 59. ISBN 978-1-4614-9155-2.
  32. ↑ Mikami, 1913, с. 53.
  33. ↑ Needham, 1959, с. 109.
  34. ↑ а б в г д Needham, 1959, с. 108—109.
  35. ↑ Martzloff, 1987, с. 142.
  36. ↑ Needham, 1959, с. 43.
  37. ↑ Needham, 1959, с. 62—63.
  38. ↑ Mikami, 1913, с. 77.
  39. ↑ Libbrecht, 1973, с. 211.
  40. ↑ Needham, 1959, с. 134—137.
  41. ↑ Needham, 1959, с. 46.
  42. ↑ а б Boyer, 1991, с. 204, "China and India".
  43. ↑ Boyer, 1991, с. 203, "China and India".
  44. ↑ Boyer, 1991, с. 205, "China and India".
  45. ↑ Boyer, 1991, с. 204—205, "China and India".
  46. ↑ Dauben, 2007, с. 308.
  47. ↑ Restivo, Sal (1992). Mathematics in Society and History: Sociological Inquiries. Dordrecht: Kluwer Academic Publishers. с. 32. ISBN 1-4020-0039-1..
  48. ↑ Gauchet, L. (1917). Note sur la trigonométrie sphérique de Kouo Cheou-king. T'oung Pao. 18 (3): 151—174. doi:10.1163/156853217X00075. ISSN 0082-5433. JSTOR 4526535.
  49. ↑ Needham, 1959, с. 109—110.
  50. ↑ Needham, 1959, с. 110.
  51. ↑ Martzloff, 1987, с. 4.
  52. ↑ He, Ji-Huan (2004). Some interpolation formulas in Chinese ancient mathematics. Applied Mathematics and Computation (англ.). 152 (2): 367—371. doi:10.1016/S0096-3003(03)00559-9. ISSN 0096-3003.
  53. ↑ Martzloff, 1987, с. 20.
  54. ↑ Martzloff, 1987, с. 21.
  55. ↑ . New York. {{cite encyclopedia}}: Пропущений або порожній |title= (довідка)
  56. ↑ Martzloff, 1987, с. 29.
  57. ↑ Martzloff, 1987, с. 25—28.
  58. ↑ Han Qi; Jami, Catherine (2003). The Reconstruction of Imperial Mathematics in China During the Kangxi Reign (1662-1722). Early Science and Medicine. 8 (2): 88—110. doi:10.1163/157338203X00026. ISSN 1383-7427.
  59. ↑ Jami, Catherine (1 грудня 2011). A mathematical scholar in Jiangnan: The first half-life of Mei Wending. The Emperor's New Mathematics: Western Learning and Imperial Authority During the Kangxi Reign (1662-1722). Oxford University Press. с. 82—101. doi:10.1093/acprof:oso/9780199601400.003.0005. ISBN 9780199601400. {{cite book}}: |access-date= вимагає |url= (довідка)
  60. ↑ Elman, Benjamin A. (2005). On their own terms: science in China, 1550-1900. Cambridge, Mass.: Harvard University Press. ISBN 9780674036475. OCLC 443109938.
  61. ↑ Martzloff, 1987, с. 28.
  62. ↑ Minghui, Hu (14 лютого 2017). China's transition to modernity : the new classical vision of Dai Zhen. Seattle. ISBN 978-0295741802. OCLC 963736201.
  63. ↑ Martzloff, 1987.
  64. ↑ Catherine, Jami (2012). The emperor's new mathematics : Western learning and imperial authority during the Kangxi Reign (1662-1722). Oxford: Oxford University Press. ISBN 9780191729218. OCLC 774104121.
  65. ↑ Carlyle, Edward Irving (1900). "Wylie, Alexander". In Lee, Sidney. Dictionary of National Biography. 63. London: Smith, Elder & Co.
  66. ↑ Martzloff, 1987, с. 341—351.
  67. ↑ Bréard, 2019.
  68. ↑ Martzloff, 1987, с. 34—39.
  69. ↑ Chern biography. www-history.mcs.st-and.ac.uk. Процитовано 16 січня 2017.
  70. ↑ 12.06.2004 - Renowned mathematician Shiing-Shen Chern, who revitalized the study of geometry, has died at 93 in Tianjin, China. www.berkeley.edu. Процитовано 16 січня 2017.
  71. ↑ Chen, J. R. (1973). On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Scientia Sinica. 16: 157—176.
  72. ↑ а б Kong, 2015.
  73. ↑ а б Kong, 2012.
  74. ↑ Team Results: China at International Mathematical Olympiad.
  75. ↑ Cullen, Christopher; Loewe, Michael (2010). Numbers, numeracy and the cosmos. У Nylan, Michael (ред.). China's early empires: a re-appraisal. University of Cambridge Oriental publications. Cambridge: Cambridge University Press. ISBN 978-0-521-85297-5.

Посилання

[ред. | ред. код]
Отримано з https://uk.wikipedia.org/wiki/Китайська_математика