Градієнтний спуск
Градіє́нтний спуск (англ. gradient descent) — це ітераційний алгоритм оптимізації першого порядку, в якому для знаходження локального мінімуму функції здійснюються кроки, пропорційні протилежному значенню градієнту (або наближеного градієнту) функції в поточній точці. Якщо натомість здійснюються кроки пропорційно самому значенню градієнту, то відбувається наближення до локального максимуму цієї функції; і ця процедура тоді відома як градіє́нтний підйо́м (англ. gradient ascent).
Градієнтний спуск відомий також як найшви́дший спуск (англ. steepest descent), або ме́тод найшви́дшого спу́ску (англ. method of steepest descent). Градієнтний спуск не слід плутати з методом перевалу[en] для наближення інтегралів.

Градієнтний спуск ґрунтується на тому спостереженні, що якщо функція кількох змінних[en] є визначеною[en] та диференційовною в околі точки , то зменшується найшвидше, якщо йти від в напрямку, протилежному градієнтові в , . З цього випливає, що якщо
для достатньо малого , то . Іншими словами, член віднімається від , оскільки ми хочемо рухатися проти градієнту, тобто вниз до мінімуму. Враховуючи це спостереження, починають з припущення про локальний мінімум , і розглядають таку послідовність , що
Ми маємо
і тому сподіваємося, що послідовність збігається до бажаного локального мінімуму. Зауважте, що значення розміру кроку (англ. step size) дозволено змінювати на кожній ітерації. Для деяких припущень стосовно функції (наприклад, що є опуклою, а задовольняє умові Ліпшиця) і певних варіантах вибору (наприклад, якщо його вибирають лінійним пошуком, який задовольняє умови Вольфе), збіжність до локального мінімуму може бути гарантовано. Якщо функція є опуклою, то всі локальні мінімуми є також і глобальними мінімумами, тому в такому випадку градієнтний спуск може збігатися до глобального розв'язку.
Цей процес проілюстровано на зображенні праворуч. Тут припускається, що визначено на площині, і що її графік має форму чаші. Сині криві є ізолініями, тобто областями, в яких значення є сталим. Червоні стрілки, які виходять з точок, показують напрям, протилежний градієнтові в цій точці. Зауважте, що (анти)градієнт у точці є ортогональним до ізолінії, яка проходить цією точкою. Видно, що спуск градієнтом веде нас до дна чаші, тобто до точки, в якій значення функції є мінімальним.
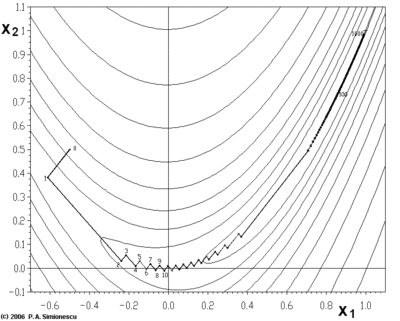
Градієнтний спуск має проблеми з патологічними функціями, такими як показана тут функція Розенброка.
Функція Розенброка має вузьку вигнуту долину, яка містить мінімум. Дно цієї долини є дуже пологим. Через вигнутість пологої долини оптимізація повільно рухається в напрямку мінімуму зиґзаґом кроками малого розміру.
«Зиґзаґоподібна» природа цього методу також є очевидною нижче, де градієнтний спуск застосовано до .


Для деяких із наведених вище прикладів градієнтний спуск є відносно повільним поблизу мінімуму: з технічної точки зору, його асимптотичний темп збігання поступається багатьом іншим методам. Для невдало обумовлених опуклих задач градієнтний спуск «зиґзаґує» все більше, коли градієнт вказує майже ортогонально до найкоротшого напряму до точки мінімуму. Докладніше див. коментарі нижче.
Для недиференційовних функцій градієнтні методи є недостатньо визначеними. Для локально ліпшицевих задач, та особливо для задач опуклої оптимізації, цілком визначеними є в'язкові методи спуску. Також можуть застосовуватися не-спускові методи, такі як методи субградієнтної проєкції.[1] Ці методи зазвичай є повільнішими за градієнтний спуск. Іншою альтернативою для недиференційовних функцій є «згладжування» цих функцій, або обмеження функції гладкою функцією. За цього підходу розв'язують згладжену задачу в надії, що відповідь для неї є близькою до відповіді на незгладжену задачу (іноді це може бути зроблено строгим).
Градієнтний спуск може застосовуватися для розв'язання системи лінійних рівнянь, переформульованого як задача квадратичної мінімізації, наприклад, із застосуванням методу найменших квадратів. Розв'язок
у сенсі методу найменших квадратів визначається як мінімізація функції
В традиційному методі найменших квадратів для дійсних та використовується евклідова норма, і в цьому випадку
В такому випадку мінімізація лінійним пошуком, яка знаходить на кожній ітерації локально оптимальний розмір кроку , може виконуватися аналітично, і явні формули локально оптимального є відомими.[2]
Для розв'язання лінійних рівнянь градієнтний спуск застосовується рідко, а однією з найпопулярніших альтернатив є метод спряжених градієнтів. Швидкість збігання градієнтного спуску залежить від максимального та мінімального власних значень , тоді як швидкість збігання спряжених градієнтів має складнішу залежність від цих власних значень, і може отримувати користь від передобумовлювання[en]. Градієнтний спуск також отримує користь від передобумовлювання, але це не роблять так поширено.
Градієнтний спуск може також застосовуватися і до розв'язання систем нелінійних рівнянь. Нижче наведено приклад, як застосовувати градієнтний спуск для розв'язання для трьох невідомих змінних, x1, x2 та x3. Цей приклад показує одну ітерацію градієнтного спуску.
Розгляньмо систему нелінійних рівнянь
припустімо, що ми маємо функцію
де
та цільову функцію
з початковим припущенням
Ми знаємо, що
де
Потім обчислімо ці члени в
Отже,
та

Тепер мусить бути знайдено придатний , такий що . Це можна зробити за допомогою будь-якого з безлічі алгоритмів лінійного пошуку. Можна також просто припустити , що дає
При обчисленні на цьому значенні
Зменшення з до значення наступного кроку є відчутним зменшенням цільової функції. Подальші кроки знижуватимуть її значення доти, доки не буде знайдено розв'язок системи.
Градієнтний спуск працює в просторах з будь-яким числом вимірів, навіть у нескінченновимірних. В останньому випадку простір пошуку зазвичай є простором функцій, і для визначення напрямку спуску здійснюється обчислення похідної Гато функціоналу, який мінімізують.[3]
Якщо кривина заданої функції дуже різниться в різних напрямках, то градієнтному спускові може знадобитися багато ітерацій для обчислення локального мінімуму з потрібною точністю. Для таких функцій повільне збігання лікується передобумовлюванням[en], яке змінює геометрію простору так, щоби надати множинам рівнів функції форми концентричних кіл. Проте побудова та застосування передобумовлювання можуть бути обчислювально витратними.
Градієнтний спуск можна поєднувати з лінійним пошуком, який на кожній ітерації шукає локально оптимальний розмір кроку . Виконання лінійного пошуку може бути витратним за часом. З іншого боку, застосування незмінного малого може давати погану збіжність.
Кращими альтернативами можуть бути методи на основі методу Ньютона та обернення гессіану із застосуванням методик спряжених градієнтів.[4][5] Загалом такі методи збігаються за меншу кількість ітерацій, але вартість кожної ітерації є вищою. Прикладом є Метод БФГШ, який складається з обчислення на кожному кроці матриці, на яку множиться вектор градієнту, щоби йти в «найкращому» напрямку, поєднаного зі складнішим алгоритмом лінійного пошуку для знаходження «найкращого» значення . Для надзвичайно великих задач, у яких домінують питання комп'ютерної пам'яті, замість БФГШ або найшвидшого спуску повинні застосовуватися методи з обмеженою пам'яттю, такі як О-БФГШ[en].
Градієнтний спуск може розглядатися як метод Ейлера для розв'язання звичайних диференційних рівнянь потоку градієнта.
Алгоритм градієнтного спуску застосовується для знаходження локального мінімуму функції f(x)=x4−3x3+2 з похідною f'(x)=4x3−9x2. Ось реалізація мовою програмування Python.
# Виходячи з обчислень, ми очікуємо, що локальний мінімум матиме місце в x=9/4
x_old = 0 # Це значення не важливе, оскільки abs(x_new - x_old) > precision
x_new = 6 # Алгоритм стартує з x=6
gamma = 0.01 # розмір кроку
precision = 0.00001
def f_derivative(x):
return 4 * x**3 - 9 * x**2
while abs(x_new - x_old) > precision:
x_old = x_new
x_new = x_old - gamma * f_derivative(x_old)
print("Локальний мінімум має місце в", x_new)
Наведений вище фрагмент коду має бути змінено по відношенню до розміру кроку відповідно до системи, яка є під руками, а збіжність може бути зроблено швидшою шляхом застосування адаптивного розміру кроку. В наведеному вище випадку розмір кроку не є адаптивним. Він залишається на рівні 0.01 в усіх напрямках, що може іноді призводити до невдачі методу за рахунок відхилення від мінімуму.
Наступний код MATLAB демонструє конкретне рішення для розв'язання системи нелінійних рівнянь, представленої в попередньому розділі:
% Багатовимірна вектор-функція G(x)
G = @(x) [
3*x(1) - cos(x(2)*x(3)) - 3/2 ;
4*x(1)^2 - 625*x(2)^2 + 2*x(2) - 1 ;
exp(-x(1)*x(2)) + 20*x(3) + (10*pi-3)/3];
% Якобіан G
JG = @(x) [
3, sin(x(2)*x(3))*x(3), sin(x(2)*x(3))*x(2) ;
8*x(1), -1250*x(2)+2, 0 ;
-x(2)*exp(-x(1)*x(2)), -x(1)*exp(-x(1)*x(2)), 20 ];
% Цільова функція F(x), яку потрібно мінімізувати, щоби розв'язати G(x)=0
F = @(x) 0.5 * sum(G(x).^2);
% Градієнт F (часткові похідні)
dF = @(x) JG(x).' * G(x);
% Параметри
GAMMA = 0.001; % розмір кроку (темп навчання)
MAX_ITER = 1000; % максимальне число ітерацій
FUNC_TOL = 0.1; % кінцеве допустиме відхилення F(x)
fvals = []; % зберігання значень F(x) протягом ітерацій
progress = @(iter,x) fprintf('iter = %3d: x = %-32s, F(x) = %f\n', ...
iter, mat2str(x,6), F(x));
% Ітерування
iter = 1; % лічильник ітерацій
x = [0; 0; 0]; % початкове припущення
fvals(iter) = F(x);
progress(iter, x);
while iter < MAX_ITER && fvals(end) > FUNC_TOL
iter = iter + 1;
x = x - GAMMA * dF(x); % градієнтний спуск
fvals(iter) = F(x); % обчислити цільову функцію
progress(iter, x); % показати перебіг
end
% Накреслити
plot(1:iter, fvals, 'LineWidth',2); grid on;
title('Objective Function'); xlabel('Iteration'); ylabel('F(x)');
% Обчислити кінцевий розв'язок системи рівнянь G(x)=0
disp('G(x) = '); disp(G(x))
% Виведення:
%
% iter = 1: x = [0;0;0] , F(x) = 58.456136
% iter = 2: x = [0.0075;0.002;-0.20944] , F(x) = 23.306394
% iter = 3: x = [0.015005;0.0015482;-0.335103] , F(x) = 10.617030
% ...
% iter = 187: x = [0.683335;0.0388258;-0.52231] , F(x) = 0.101161
% iter = 188: x = [0.684666;0.0389831;-0.522302] , F(x) = 0.099372
%
% (збіглося за 188 ітерацій після перевищення кінцевого допустимого відхилення F(x))
Градієнтний спуск може бути розширено для підтримки обмежень шляхом включення проєкції на множину обмежень. Цей метод підходить лише тоді, коли ця проєкція є ефективно обчислюваною на комп'ютері. За зручних припущень цей метод збігається. Цей метод є окремим випадком послідовно-зворотного алгоритму для монотонних включень (який включає опукле програмування та варіаційні нерівності[en]).[6]
Інше розширення градієнтного спуску виникло завдяки Юрієві Нестерову[en] 1983 року,[7] і було згодом узагальнене. Він пропонує просту видозміну цього алгоритму, яка уможливлює швидке збігання для опуклих задач. А саме, якщо функція є опуклою, а є ліпшицевою, і немає припущення, що є сильно опуклою, то похибку цільового значення, породжувану методом градієнтного спуску на кожному кроці , буде обмежено . Із застосуванням методики прискорення Нестерова похибка знижується до .[8]
Ще одним розширенням, яке знижує ризик застрягнути в локальному мінімумі, а також істотно прискорює збіжність у випадках, коли інакше процес би сильно зиґзаґував, є метод імпульсу (англ. momentum method), який використовує член імпульсу по аналогії з «масою ньютонових частинок, які рухаються в'язким середовищем у консервативному силовому полі».[9] Цей метод часто використовують як розширення алгоритмів зворотного поширення, що застосовуються для тренування штучних нейронних мереж.[10][11]
- Метод спряженого градієнта
- Метод проксимального градієнта
- Стохастичний градієнтний спуск
- Rprop[en]
- Дельта-правило
- Умови Вольфе
- Передобумовлювання[en]
- Метод БФГШ
- Метод Нелдера – Міда
- Алгоритм Франк — Вульфа
- ↑ Kiwiel, Krzysztof C. (2001). Convergence and efficiency of subgradient methods for quasiconvex minimization. Mathematical Programming (Series A). Т. 90, № 1. Berlin, Heidelberg: Springer. с. 1—25. doi:10.1007/PL00011414. ISSN 0025-5610. MR 1819784. (англ.)
- ↑ Yuan, Ya-xiang (1999). Step-sizes for the gradient method (PDF). AMS/IP Studies in Advanced Mathematics. Providence, RI: American Mathematical Society. 42 (2): 785.
{{cite journal}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) (англ.) - ↑ G. P. Akilov, L. V. Kantorovich, Functional Analysis, Pergamon Pr; 2 Sub edition, ISBN 0-08-023036-9, 1982 (англ.)
- ↑ W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, 2nd Ed., Cambridge University Press, New York, 1992 (англ.)
- ↑ T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition, Springer Vieweg, 2016, ISBN 978-3-658-11455-8. (англ.)
- ↑ P. L. Combettes and J.-C. Pesquet, «Proximal splitting methods in signal processing» [Архівовано 7 липня 2011 у Wayback Machine.], in: Fixed-Point Algorithms for Inverse Problems in Science and Engineering, (H. H. Bauschke, R. S. Burachik, P. L. Combettes, V. Elser, D. R. Luke, and H. Wolkowicz, Editors), pp. 185—212. Springer, New York, 2011. (англ.)
- ↑ Yu. Nesterov, «Introductory Lectures on Convex Optimization. A Basic Course» (Springer, 2004, ISBN 1-4020-7553-7) (англ.)
- ↑ Fast Gradient Methods [Архівовано 24 грудня 2012 у Wayback Machine.], lecture notes by Prof. Lieven Vandenberghe for EE236C at UCLA (англ.)
- ↑ Qian, Ning (January 1999). On the momentum term in gradient descent learning algorithms (PDF). Neural Networks[en]. 12 (1): 145—151. Архів оригіналу (PDF) за 8 травня 2014. Процитовано 17 жовтня 2014. (англ.)
- ↑ Momentum and Learning Rate Adaptation. Willamette University[en]. Архів оригіналу за 21 жовтня 2014. Процитовано 17 жовтня 2014. (англ.)
- ↑ Geoffrey Hinton; Nitish Srivastava; Kevin Swersky. 6 — 3 — The momentum method. YouTube. Архів оригіналу за 10 травня 2015. Процитовано 18 жовтня 2014. Частина з серії лекцій для онлайн-курсу Coursera Neural Networks for Machine Learning [Архівовано 29 червня 2016 у Wayback Machine.]. (англ.)
- Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0. (англ.)
- Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8 (англ.)
- Raad Z. Homod, K. S. M. Sahari, H. A.F. Almurib, F. H. Nagi, Gradient auto-tuned Takagi-Sugeno fuzzy forward control of a HVAC system using predicted mean vote index Energy and Buildings, 49 (6) (2012) 254—267 [Архівовано 11 грудня 2018 у Wayback Machine.] (англ.)
- Cauchy, Augustin (1847). Méthode générale pour la résolution des systèmes d'équations simultanées. с. 536—538. Архів оригіналу за 13 жовтня 2016. Процитовано 31 липня 2016. (фр.)
- Енциклопедія кібернетики : у 2 т. / за ред. В. М. Глушкова. — Київ : Гол. ред. Української радянської енциклопедії, 1973., Поляк Р. А., Примак М. Е., т. 2, ст. 64.