Тетрагемігексаедр
| Тетрагемігексаедр | |
|---|---|

| |
| Тип | однорідний зірчастий многогранник |
| Елемент | граней 7, ребер 12, вершин 6 |
| Ейлерова характеристика |
= 1 |
| Граней за числом сторін | 4{3}+ 3{4} |
| Символ Вітгоффа | 2 (подвійне накриття) |
| Група симетрії | Td, [3,3], *332 |
| Позначення | U04, C36, W67 |
| Двоїстий | тетрагемігексакрон |
| Вершинна фігура |  3.4.3/2.4 |
| Скорочена назва Бауера | Thah |
Тетрагемігексаедр, або гемікубооктаедр, — однорідний зірчастий многогранник, що має номер U4. Має 6 вершин, 12 ребер, і 7 граней — 4 трикутних і 3 квадратних. Його вершинною фігурою є схрещений чотирикутник. Діаграма Коксетера — Динкіна — ![]()
![]()
![]()
![]()
![]()
![]()
![]() (хоча ця діаграма відповідає подвійному покриттю тетрагемігексаедра).
(хоча ця діаграма відповідає подвійному покриттю тетрагемігексаедра).
Це єдиний непризматичний однорідний многогранник з непарним числом граней. Його символ Вітгоффа[en] рівний 3/2 3 | 2, але насправді цей символ відповідає подвійному покриттю тетрагемігексаедра 8 трикутниками і 6 квадратами, які попарно збігаються в просторі. (Це можна розглядати інтуїтивно як два суміщені тетрагемігексаедри.)
Многогранник є гемімногогранником (напівмногогранником[en]). Префікс «гемі-» означає, що деякі грані утворюють групу вдвічі меншого розміру, ніж відповідний правильний многогранник. У цьому випадку три квадратні грані утворюють групу, що має вдвічі менше граней, ніж правильний гексаедр (шестигранник), відомий як куб, звідси й назва гемігексаедр. Гемі-грані орієнтовані в тому ж напрямку, що й грані правильного многогранника. Три квадратні грані тетрагемігексаедра, як і три орієнтації граней куба, взаємно перпендикулярні.
Характеристика «наполовину менше» також означає, що гемі-грані мають проходити через центр многогранника, де вони всі перетинаються. Візуально, кожен квадрат ділиться на чотири прямокутних трикутники, з яких з кожного боку видно лише два.
Багатогранник має неорієнтовану поверхню. Він є унікальним, оскільки з усіх однорідних многогранників тільки він має ейлерову характеристику 1, а тому є проєктивним многогранником[en], що подає дійсну проєктивну площину, подібно до римської поверхні[en].
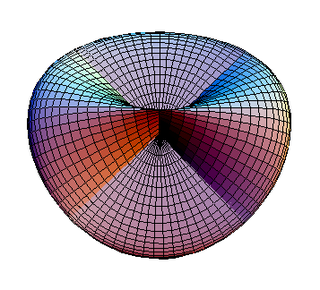 Римська поверхня[en] |
Багатогранник має ті ж вершини й ребра, що й правильний октаедр. Чотири його трикутні грані збігаються з 4 з 8 трикутних граней октаедра, але додаткові квадратні грані проходять через центр многогранника.
 Октаедр |
 Тетрагемігексаедр |
Двоїстим многогранником є тетрагемігексакрон.
Многогранник двічі накритий кубооктаедром[1], який має ту саму абстрактну вершинну фігуру (2 трикутники і два квадрати: 3.4.3.4) та подвоєне число вершин, ребер і граней. Він має ту саму топологію, що й абстрактний многогранник гемікубооктаедр.
 Кубооктаедр |
 Тетрагемігексаедр |
Його можна побудувати як схрещений трикутний куполоїд. Усі куплоїди та двоїсті їм многогранники топологічно є проєктивними площинами[2].
| n / d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  Перехрещений трикутний куполоїд {3/2} |
 Пентаграмний куполоїд {5/2} |
 Гептаграмний куполоїд {7/2} |
| 4 | — |  Перехрещений пентаграмний куполоїд {5/4} |
 Перехрещений гептаграмний куполоїд {7/4} |
| Тетрагемігексакрон | |
|---|---|

| |
| Тип | зірчастий многогранник |
| Елемент | граней 6, ребер 12, вершин 7 |
| Ейлерова характеристика | = 1 |
| Група симетрії | Td, [3,3], *332 |
| Позначення | DU04 |
| Двоїстий | тетрагемігексаедр |
Тетрагемігексакрон є двоїстим для тетрагемігексаедра і одним з дев'яти двоїстих гемімногогранників[en].
Оскільки гемімногогранники мають грані, що проходять через центр, двоїсті фігури мають відповідні вершини в нескінченності. Строго кажучи, в нескінченній точці дійсної проєктивної площини[3]. У книзі Маґнуса Веннинґера Dual Models їх напедено як перетинні призми, кожна з яких йде в нескінченність в обох напрямках. На практиці моделі призм обрізають у деякій точці, зручній для творця моделі. Веннінґер запропонував вважати ці фігури членами нового класу зірчастих фігур, які назвав зірчасті до нескінченності. Однак він також додав, що, строго кажучи, вони не є многогранниками, оскільки не задовольняють звичним визначенням.
Вважають, що топологічно многогранник містить 7 вершин. Три вершини вважають такими, що лежать у нескінченності (дійсної проєктивної площини) і відповідають безпосередньо трьом вершинам геміоктаедра[en], абстрактного многогранника. Інші чотири вершини є кутами альтернованого центрального куба (напівкуба[en], в нашому випадку тетраедра).
- ↑ Richter.
- ↑ Polyhedral Models of the Projective Plane, Paul Gailiunas, Bridges 2018 Conference Proceedings
- ↑ Wenninger, 2003, с. 101.
- David A. Richter. Two Models of the Real Projective Plane.
- Magnus Wenninger. Dual Models. — Cambridge University Press, 2003. — ISBN 978-0-521-54325-5. (Стор. 101, Duals of the (nine) hemipolyhedra)
- Weisstein, Eric W. Тетрагемігексаедр(англ.) на сайті Wolfram MathWorld.
- Weisstein, Eric W. Однорідний многогранник(англ.) на сайті Wolfram MathWorld.
- Paper model
- Great Stella: software used to create main image on this page

