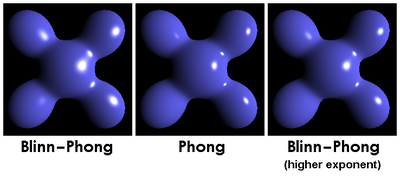
Модель відбиття Бліна-Фонга

Модель відбиття Блінна–Фонга, яка також називається модифікованою моделлю відбиття Фонга, є модифікацією моделі відбиття Фонга, що була розроблена Джимом Блінном.

Затінення Блінна-Фонга — це модель затінення, яка використовується в фіксованому конвеєрі OpenGL і Direct3D (до Direct3D 10 і OpenGL 3.1). Значення освітлення обчислюється на кожній вершині, коли вона проходить по графічному конвеєру; значення пікселів між вершинами інтерполюються за затіненням Гуро за замовчуванням, а не більш дорогим затіненням Фонга.

Опис

Вектори для розрахунку затінення Фонга та Блінна–Фонга

У затіненні Фонга потрібно постійно перераховувати скалярний добуток $R\cdot V$ між напрямом погляду спостерігача (V) і променем від джерела світла (L), відбитим (R) від поверхні.

Якщо натомість обчислити половинний вектор між вектором спостерігача та вектором джерела світла,

$H={\frac {L+V}{\left\|L+V\right\|}}.$

$R\cdot V$ можна замінити на $N\cdot H$, де $N$ — нормована нормаль поверхні. У наведеному вище рівнянні $L$ і $V$ є нормованими векторами і $H$ є розв’язком рівняння $V=P_{H}(-L),$ де $P_{H}$ — це матриця Хаусхолдера, яка відображає точку на гіперплощині, яка містить початок координат і має нормаль $H.$

Цей скалярний добуток рівний косинусу кута, який становить половину кута, представленого скалярним добутком Фонга, якщо $V$, $L$, $N$ і $R$ лежать в одній площині. Це співвідношення між кутами залишається приблизно вірним, коли вектори не лежать в одній площині, особливо коли кути малі. Тому кут між $N$ і $H$ іноді називають половинним кутом.

Враховуючи, що кут між половинним вектором і нормаллю поверхні, ймовірно, буде меншим, ніж кут між $R$ і $V$, який використовується в моделі Фонга (якщо поверхня не розглядається під дуже крутим кутом, для якого він, імовірно, буде більшим), і, оскільки, в моделі Фонга використовується $\left(R\cdot V\right)^{\alpha },$ експоненту можна встановити $\alpha ^{\prime }>\alpha$ таку, що $\left(N\cdot H\right)^{\alpha ^{\prime }}$ ближче до попереднього виразу.

Для поверхонь, які засвічені в бік глядача (дзеркальне відображення на поверхнях, звернених до глядача), $\alpha ^{\prime }=4\,\alpha$ призведе до дзеркальних відблисків, які сильно схожі на відповідні відблиски в відображенні Фонга. Однак, у той час як відблиски Фонга завжди мають круглу форму для плоскої поверхні, відблиски Блінна–Фонга стають еліптичними, коли на поверхню дивляться під крутим кутом. Це схоже на випадки, коли сонце відбивається в морі близько до горизонту, або коли віддалений вуличний ліхтар відбивається у мокрому тротуарі, де відображення завжди буде набагато більш розширеним по вертикалі, ніж по горизонталі.

Крім того, хоча цю модель можна розглядати як наближення до моделі Фонга, вона створює більш точні моделі емпірично визначених двопроменевих функцій відбивної здатності, ніж модель Фонга для багатьох типів поверхонь.

Ефективність

Модель Блінна-Фонга буде швидшою за модель Фонга у випадку, коли спостерігач і світло вважаються дуже віддаленими від об'єкту спостереження, наприклад, на відстані, що наближається до нескінченності, або рівній нескінченності. Це працює в випадку спрямованого світла та ортографічної/ізометричної камери. У цьому випадку половинний вектор не залежить від позиції та кривизни поверхні тому, що половинний вектор залежить від напрямку до позиції спостерігача та напрямку до позиції світла, які окремо сходяться на віддаленій відстані, отже, половинний вектор можна вважати константним у цьому випадку. $H$ отже, може бути обчислено один раз для кожного джерела світла, а потім використано для всього кадру, або тоді, коли світло та точка огляду залишаються в тому самому відносному положенні. Те саме не стосується методу Фонга з використанням вектора відбиття, який залежить від кривизни поверхні та повинен бути перерахований для кожного пікселя зображення (або для кожної вершини моделі у випадку вершинного освітлення). У 3D-сценах із камерами, що мають перспективу, ця оптимізація неможлива.

Зразки коду

Приклад коду мовою HLSL

Цей зразок на мові HLSL є методом обчислення розсіяного та дзеркального світла від точкового джерела освітлення. Вхідними даними є структура даних для джерела світла, положення поверхні в просторі, вектор напрямку до спостерігача і нормаль поверхні. Структура даних з освітленням поверхні повертається;

В коді нижче, також, потрібно обмежити значення скалярного добутку до нуля у випадку негативних значень. Без цього, світло, що спрямовується від камери, розглядається так само, як світло, що спрямовується до неї. При розрахунку дзеркального відображення неправильний «ореол» світла, що відбивається від країв об’єкта та від камери, може виглядати таким же яскравим, як і світло, яке безпосередньо відбивається в бік на камеру.

struct Lighting
{
    float3 Diffuse;
    float3 Specular;
};

struct PointLight
{
	float3 position;
	float3 diffuseColor;
	float  diffusePower;
	float3 specularColor;
	float  specularPower;
};

Lighting GetPointLight(PointLight light, float3 pos3D, float3 viewDir, float3 normal)
{
	Lighting OUT;
	if (light.diffusePower > 0)
	{
		float3 lightDir = light.position - pos3D; //3D position in space of the surface
		float distance = length(lightDir);
		lightDir = lightDir / distance; // = normalize(lightDir);
		distance = distance * distance;

		//Інтенсивність розсіяного світла. Функція saturate для того, щоб значення було в рамках 0 та 1.
		float NdotL = dot(normal, lightDir);
		float diffuseIntensity = saturate(NdotL);

		// Розрахунок розсіяного світла враховуючи колір світла, ступінь розсіяного світла та затухання
		OUT.Diffuse = diffuseIntensity * light.diffuseColor * light.diffusePower / distance;

		//Розрахунок половинного вектору між напрямом світла та напрямом до спостерігача
		float3 H = normalize(lightDir + viewDir);

		//Інтенсивність відблисків
		float NdotH = dot(normal, H);
		float specularIntensity = pow(saturate(NdotH), specularHardness);

		//Обчислення відблиску враховуючи всі параметри
		OUT.Specular = specularIntensity * light.specularColor * light.specularPower / distance; 
	}
	return OUT;
}

Приклад коду мовою GLSL

Цей зразок на мові GLSL складається з двох файлів коду, або шейдерів . Перший є так званим вершинним шейдером і реалізує модель затінення Фонга, яка використовується для інтерполяції нормалі поверхні між вершинами. Другий шейдер є так званим фрагментним шейдером і реалізує модель затінення Блінна–Фонга для визначення розсіяного та дзеркального світла від точкового джерела світла.

Вершиний шейдер

Цей вершинний шейдер реалізує затінення Фонга :

attribute vec3 inputPosition;
attribute vec3 inputNormal;

uniform mat4 projection, modelview, normalMat;

varying vec3 normalInterp;
varying vec3 vertPos;

void main() {
    gl_Position = projection * modelview * vec4(inputPosition, 1.0);
    vec4 vertPos4 = modelview * vec4(inputPosition, 1.0);
    vertPos = vec3(vertPos4) / vertPos4.w;
    normalInterp = vec3(normalMat * vec4(inputNormal, 0.0));
}

Фрагментний шейдер

Цей фрагментний шейдер реалізує модель затінення Блінна–Фонга та гамма-корекцію :

precision mediump float;

in vec3 normalInterp;
in vec3 vertPos;

uniform int mode;

const vec3 lightPos = vec3(1.0, 1.0, 1.0);
const vec3 lightColor = vec3(1.0, 1.0, 1.0);
const float lightPower = 40.0;
const vec3 ambientColor = vec3(0.1, 0.0, 0.0);
const vec3 diffuseColor = vec3(0.5, 0.0, 0.0);
const vec3 specColor = vec3(1.0, 1.0, 1.0);
const float shininess = 16.0;
const float screenGamma = 2.2; // Припустімо, що монітор відкалібровано відповідно до колірного простору sRGB

void main() {

  vec3 normal = normalize(normalInterp);
  vec3 lightDir = lightPos - vertPos;
  float distance = dot(lightDir, lightDir);
  lightDir = normalize(lightDir);

  float lambertian = max(dot(lightDir, normal), 0.0);
  float specular = 0.0;

  if (lambertian > 0.0) {

    vec3 viewDir = normalize(-vertPos);

    // це модель Блінна-Фонга
    vec3 halfDir = normalize(lightDir + viewDir);
    float specAngle = max(dot(halfDir, normal), 0.0);
    specular = pow(specAngle, shininess);
       
    // Це модель Фонга (для порівняння)
    if (mode == 2) {
      vec3 reflectDir = reflect(-lightDir, normal);
      specAngle = max(dot(reflectDir, viewDir), 0.0);
      // note that the exponent is different here
      specular = pow(specAngle, shininess/4.0);
    }
  }
  vec3 colorLinear = ambientColor +
                     diffuseColor * lambertian * lightColor * lightPower / distance +
                     specColor * specular * lightColor * lightPower / distance;
  // застосовуємо гамма-корекцію (припускаємо, що ambientColor, diffuseColor та specColor
  // знаходяться в лінійному просторі, тобто не мають гамма-корекції)
  vec3 colorGammaCorrected = pow(colorLinear, vec3(1.0 / screenGamma));
  // повертаємо колір після гамма-корекції
  gl_FragColor = vec4(colorGammaCorrected, 1.0);
}

На кольори ambientColor ,diffuseColor і specColor гамма-корекція не повинна застосовуватися . Якщо це кольори, отримані з файлів зображень з гамма-корекцією (JPEG, PNG тощо), їх потрібно лінеаризувати перед роботою з ними, що робиться шляхом масштабування значень каналів кольору до діапазону [0, 1] і піднесення їх до степеня, рівному значенню гамми зображення, яке для зображень у просторі кольорів sRGB можна вважати рівним приблизно 2.2 (хоча для цього конкретного простору кольорів просте співвідношення степенів є лише наближенням фактичного перетворення). Сучасні графічні API мають можливість автоматично виконувати цю гамма-корекцію під час читання пікселя з текстури або запису в буфер кадру.

Див. також

• Cписок поширених алгоритмів затінення
• Модель відбиття Фонга для відповідної моделі Фонга
• Гамма-корекція
• Дзеркальне підсвічування