Наближення порожньої ґратки

Наближення порожньої ґратки — це модель зонної теорії кристалів, в якій потенціал кристалічної ґратки періодичний та ґранично слабкий. Енергія електронів у «порожній ґратці» точно така сама, як і вільних електронів. Головним здобутком такого підходу є схема класифікації електронних зон, а практично застосовними є лише його розширення, зокрема, у вигляді ґраничних випадків майже вільних електронів та сильного зв'язку.

Розсіювання та періодичність

Зони вільних електронів в одновимірній порожній ґратці у схемі повторюваної зони (ліворуч) та зведеної зони (праворуч).

Розсіювання електронів на вузлах ґратки визначається просторовим розташуванням вузлів. Кожен вузол є потенціальною ямою, на якій з певною ймовірністю відбудеться акт розсіювання. Для частинки в одновимірній ґратці, зокрема, модель Кроніга-Пенні дає можливість аналітично обчислити зонну структуру за відомими значеннями потенціалу, відстані між сусідніми атомами та розміру потенціальної ями. Для дво- і тривимірних випадків подібні моделі з невеликою кількістю параметрів дають нереалістичні розв'язки. Тим не менше, в більшості областей зонну структуру вдається наближено описати за допомогою теорії збурень, починаючи з розв'язків для порожньої ґратки, тобто плоских хвиль.

В наближенні порожньої ґратки електрони мають лише кінетичну енергію й закон дисперсії виглядає так:

$E(\mathbf {k} )={\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m}}$.

Тут $\hbar$ — зведена стала Планка, m — маса електрона, $\mathbf {k}$ — вектор оберненого простору, який називають квазіімпульсом.

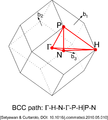
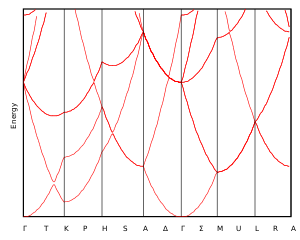
Якою малою не була би глибина потенціальної ями, у нескінченній періодичній ґратці рано чи пізно акт взаємодії відбудеться й хвилю буде відбито. Такий процес розсіювання зумовлює відомий закон Брегга, а також періодичність закону дисперсії електронів і поділ $\mathbf {k}$-простору на зони Бріллюена. Періодичність закону дисперсії математично виражається так. Якщо два $\mathbf {k}$-вектори різняться на будь-який вектор $\mathbf {G}$ оберненої гратки, $\mathbf {k} =\mathbf {k'} +\mathbf {G}$, то їм відповідає одне й те саме значення енергії, $E(\mathbf {k} )=E(\mathbf {k'} )$.

Завдяки цій періодичності для маркування всіх точок $E(\mathbf {k} )$ достатньо обмежитися такими значеннями $\mathbf {k}$, які лежать всередині першої зони Бріллюена; в поданому прикладі одновимірної лінійної ґратки зі сталою ґратки $a$ це значення $-{\frac {\pi }{a}}\leq k\leq {\frac {\pi }{a}}$. В такий спосіб у схемі зведених зон з'являються різні гілки закону дисперсії, їх доводиться додатково нумерувати: $E_{n}(\mathbf {k} )$.

Енергетичні зони й густина станів

Густина станів вільних електронів у тривимірному k-просторі

Густина станів (англ. DOS) — це кількість електронних станів в інтервалі енергій $[E,E+dE]$, пронумерованому векторами $[\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]$ оберненого простору. В одновимірному випадку густина станів, створювана зоною $E_{n}(k)$ при даній енергії $E_{0}$, тим більша, чим менше значення похідної $\left.{\frac {dE_{n}(k)}{dk}}\right|_{k_{0}:E_{n}(k_{0})=E_{0}}$.

Хоча елементарні комірки не є сферично симетричними, в наближеннях порожньої ґратки та майже вільних електронів квадратичний вигляд закону дисперсії зберігається. Порівняно з одновимірним, у дво- й тривимірному випадках кількість станів, що потрапляють в інтервал $[\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]$, збільшується внаслідок можливого виродження по напрямку вектора $\mathbf {k}$. Для тривимірної ґратки густина станів $D_{3}\left(E\right)$ пропорційна кореню квадратному з енергії, який при квадратичному законі дисперсії у свою чергу пропорційний квазіімпульсу:

$D_{3}\left(E\right)\sim {\sqrt {E}}\sim \lVert \mathbf {k} \rVert$.

Друга й вищі зони Бріллюена

Вільні електрони, що рухаються порожньою ґраткою із хвильовим вектором $\mathbf {k}$ поза першою зоною Бріллюена, будуть відбиті до першої зони Бріллюена. Хоча $\mathbf {k}$ дуже схожий на вектор імпульсу, зберігається лише квазіімпульс, тобто $\mathbf {k}$ зберігається з точністю до $\mathbf {G}$, будь-якого вектору зворотної ґратки. В зовнішніх посиланнях можна знайти онлайн-ресурси із прикладами та зображеннями вищих зон Бріллюена.

Модель майже вільних електронів

В багатьох звичайних металах, на кшталт алюмінію, ефект екранування значно послаблює електростатичне поле, створюване іонами ґратки при металічному зв'язку. Електростатичний потенціал в кристалі виражається як

$V(r)={\frac {Ze}{r}}e^{-qr}$,

де Z — атомний номер металу, e — елементарний заряд, r — відстань між електроном і ядром іона, q — параметр екранування, що обмежує дальнодію потенціалу. Перетворення Фур'є, $U_{\mathbf {G} }$, потенціалу ґратки $V(\mathbf {r} )$ дається формулою

$U_{\mathbf {G} }(q)={\frac {4\pi Ze}{q^{2}+G^{2}}}$.

Значення недіагональних елементів потенціалу $U_{\mathbf {G} }$ (між різними векторами зворотної ґратки) майже дорівнюють нулю. В результаті величина забороненої зони $2|U_{\mathbf {G} }|$ спадає й результат стає подібним до передбаченого в наближенні порожньої ґратки.

Електронні зони поширених ґраток металів

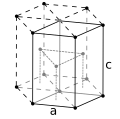
За винятком кількох екзотичних структур, переважна більшість металів кристалізується в одному з трьох структурних типів: об'ємноцентрована чи гранецентрована кубічна структура, або щільноупакована гексагональна структура.

• 
  Об'ємноцентрована кубічна (ОЦК, символ I)
• 
  Гранецентрована кубічна (ГЦК, символ F)
• 
  Гексагональна щільноупакована
• 
  Перша зона Бріллюена ОЦК ґратки
• 
  Перша зона Бріллюена ГЦК ґратки
• 
  Перша зона Бріллюена ГЩ ґратки

Зони вільних електронів в ОЦК кристалічній структурі

Зони вільних електронів в ГЦК кристалічній структурі

Зони вільних електронів в гексагональній щільноупакованій кристалічній структурі

Зовнішні посилання

• Тривимірні зображення зон Бріллюена (Техніон) [Архівовано 5 грудня 2006 у Wayback Machine.]
• Онлайн-побудова зображень зон Бріллюена [Архівовано 11 серпня 2020 у Wayback Machine.]
• Програма на Python для побудови зображень зон Бріллюена [Архівовано 8 жовтня 2021 у Wayback Machine.]