Теорема котангенсів
| Тригонометрія |
|---|
 |
| Посилання |
| Закони і теореми |
| Обчислення |
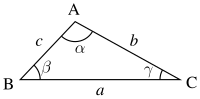
У тригонометрії, теорема котангенсів пов'язує радіус кола, вписаного у трикутник, з довжиною його сторін. Теорему котангенсів зручно використовувати при розв'язуванні трикутника за трьома сторонами.
Нехай , і — довжини трьох сторін трикутника, і — кути, що лежать навпроти, відповідно, сторін , і відповідно.
Теорема котангенсів стверджує, що якщо
- (радіус кола, вписаного у трикутник) і
- (півпериметр трикутника),
то справедливі наступні формули:[1]
звідки слідує, що
- .
Словами теорему можна сформулювати так: котангенс половинного кута дорівнює відношенню півпериметра мінус довжина протилежної сторони вказаного кута до радіуса вписаного кола.
У сферичній тригонометрії існує схожа формула для половини кута, а також двоїста до неї формула половини сторони[ru].
- ↑ The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |










