Теорема синусів

Теорема синусів — наступне тригонометричне твердження про властивості кутів та сторін довільного трикутника: нехай a, b і c є сторонами трикутника, а A, B і C — кути протилежні вказаним сторонам, тоді

${\sin A \over a}={\sin B \over b}={\sin C \over c}$

Обернене значення числа в теоремі синусів (тобто a/sin(A)) дорівнює діаметру D (або ж 2-ом радіусам) описаного навколо трикутника кола (єдине коло, що проходить через три точки A, B і C). Таким чином теорему можна переписати у розширеній формі

${a \over \sin A}={b \over \sin B}={c \over \sin C}=D=2R$

Наслідком теореми синусів є наступне твердження:

• У трикутнику навпроти більшого кута лежить більша сторона, навпроти більшої сторони лежить більший кут.

Розв'язання трикутників

Теорему синусів використовують при розв'язуванні трикутників:

1. Якщо відомі сторона a та два прилеглі кути β і γ довільного трикутника, то інші дві сторони можемо знайти із співвідношення:

$b=a\cdot {\frac {\sin \beta }{\sin \alpha }}=a\cdot {\frac {\sin \beta }{\sin \left(\pi -\beta -\gamma \right)}}$;

$c=a\cdot {\frac {\sin \gamma }{\sin \alpha }}=a\cdot {\frac {\sin \gamma }{\sin \left(\pi -\beta -\gamma \right)}}$.

Це є типовою проблемою, що постає при тріангуляції.

2. Якщо відомі дві сторони та один із кутів, що не утворюється цими сторонами

Зазначена формула дає два можливих значення для внутрішнього кута. В цьому випадку, часто лишень одне значення задовольняє умові, що сума трьох кутів трикутника дорівнює 180°; інакше отримаємо два можливих розв'язки.

Доведення

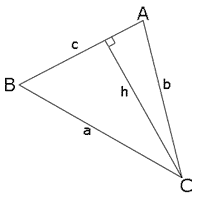
Нехай дано трикутник зі сторонами a, b, і c, з протилежними до них кутами A, B, і C. Опустимо перпендикуляр довжиною h з C на c.

Бачимо, що, за означенням:

$\sin A={\frac {h}{b}}$ та $\;\sin B={\frac {h}{a}}$

Звідси:

$h=b\,\sin A=a\,\sin B$

також

${\frac {\sin A}{a}}={\frac {\sin B}{b}}$

Повторимо операцію з кутом A і стороною a, і дістанемо:

${\frac {\sin B}{b}}={\frac {\sin C}{c}}$.∎

Доведення розширеної форми теореми синусів

Достатньо довести, що

${\frac {a}{\sin \alpha }}=2R.$

Проведемо діаметр $|BG|$ описаного кола.

За властивістю кутів, вписаних у коло, кут $GCB$ прямий, а кут $CGB$ дорівнює або $\alpha$, якщо точки $A$ і $G$ лежать по один бік від прямої $BC$, або $\pi -\alpha$ в іншому разі.

Оскільки $\sin(\pi -\alpha )=\sin \alpha$, в обох випадках маємо

$a=2R\sin \alpha$.

Повторивши ці міркування для двох інших сторін трикутника, маємо:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.$ ∎

Доведення через формули знаходження площі трикутника  

Візьмемо дві формули для знаходження площі трикутника $S={\frac {abc}{4R}}$ і $S={\frac {1}{2}}ab\sin \gamma .$

${\begin{cases}{\frac {abc}{4R}}={\frac {1}{2}}ab\sin \gamma \\{\frac {abc}{4R}}={\frac {1}{2}}ac\sin \beta \\{\frac {abc}{4R}}={\frac {1}{2}}bc\sin \alpha \end{cases}}\Leftrightarrow {\begin{cases}{\frac {c}{2R}}=\sin \gamma \\{\frac {b}{2R}}=\sin \beta \\{\frac {a}{2R}}=\sin \alpha \end{cases}}\Leftrightarrow {\begin{cases}2R={\frac {c}{\sin \gamma }}\\2R={\frac {b}{\sin \beta }}\\2R={\frac {a}{\sin \alpha }}\end{cases}}\Leftrightarrow 2R={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.$ ∎

Варіації та узагальнення

• У симплексі

$V_{n}={\frac {n-1}{n}}\cdot {\frac {{V_{n-1}^{i}}{V_{n-1}^{j}}}{V_{n-2}^{i,j}}}\cdot \sin {A_{i,j}},$

де $A_{i,j}$ — кут між гранями $V_{n-1}^{i}$ і $V_{n-1}^{j}$; $V_{n-2}^{i,j}$ — спільна грань $V_{n-1}^{i}$ і $V_{n-1}^{j}$; $V_{n}$ — об'єм симплекса.

Теорема синусів для сферичного трикутника

Ця теорема справедлива для трикутників на сфері, сторонами яких є дуги великих кіл сфери.

Нехай дано сферу одиничного радіуса і трикутник на ній, утворений перетином трьох її великих кіл. Нехай a, b і c — довжини дуг, які є сторонами трикутника. Оскільки сфера є одиничною, то a, b і c виражають кути з вершиною у центрі сфери між двома її радіусами, стягнуті цими дугами в радіанах.

Нехай A, B і C — кути, протилежні цим сторонам, тобто це двогранні кути між площинами трьох великих кіл.

Тоді, для сферичного трикутника справедливе твердження: $${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.$$

Доведення через вектори

Розглянемо сферу одиничного радіуса з центром О в початку координат. OA, OB та OC — одиничні вектори, проведені від початку координат до вершин A, B, C трикутника. Отже, кути α, β і γ є кутами a, b і c відповідно. Дуга BC утворює кут величиною a з вершиною у центрі сфери.

Введемо декартову систему координат так, щоб її вісь z проходила вздовж вектора OA. Вектор OB в площині xz утворює кут утворює кут c з віссю z та проектується на відрізок OМ у площині xy. Вектор OC утворює кут b з віссю z та проектується на ON у площині xy, а кут між ON та віссю x дорівнює A. Отже, три вектори мають координати:

$$\mathbf {OA} ={\begin{pmatrix}0\\0\\1\end{pmatrix}},\quad \mathbf {OB} ={\begin{pmatrix}\sin c\\0\\\cos c\end{pmatrix}},\quad \mathbf {OC} ={\begin{pmatrix}\sin b\cos A\\\sin b\sin A\\\cos b\end{pmatrix}}.$$

Змішаний добуток трьох векторів, OA ⋅ (OB × OC), дорівнює об'єму паралелепіпеда, побудованого на векторах OA, OB та OC. Цей об'єм є інваріантним до конкретної системи координат, яка використовується для представлення OA, OB і OC.

Значення змішаного добутку трьох векторів OA ⋅ (OB × OC) є 3 × 3 — визначником, рядками якого є координати векторів OA, OB і OC.

З віссю z вздовж OA квадрат цього визначника дорівнює

$${\begin{aligned}{\bigl (}\mathbf {OA} \cdot (\mathbf {OB} \times \mathbf {OC} ){\bigr )}^{2}&=\left(\det {\begin{pmatrix}\mathbf {OA} &\mathbf {OB} &\mathbf {OC} \end{pmatrix}}\right)^{2}\\[4pt]&={\begin{vmatrix}0&0&1\\\sin c&0&\cos c\\\sin b\cos A&\sin b\sin A&\cos b\end{vmatrix}}^{2}=\left(\sin b\sin c\sin A\right)^{2}.\end{aligned}}$$

Якщо повторити це обчислення з віссю z вздовж OB, отримаємо (sin c sin a sin B)², а з віссю z вздовж OC — (sin a sin b sin C)².

Прирівнюємо ці вирази та ділимо їх на (sin a sin b sin c)²: $${\frac {\sin ^{2}A}{\sin ^{2}a}}={\frac {\sin ^{2}B}{\sin ^{2}b}}={\frac {\sin ^{2}C}{\sin ^{2}c}}={\frac {V^{2}}{\sin ^{2}(a)\sin ^{2}(b)\sin ^{2}(c)}},$$ де V — об'єм паралелепіпеда, побудованого на векторах OA, OB та OC, що відповідають вершинам сферичного трикутника.

Легко побачити, що для малих сферичних трикутників, коли радіус сфери значно перевищує довжини сторін трикутника, ця формула в граничному значенні переходить в формулу для плоского трикутника, оскільки

$$\lim _{a\to 0}{\frac {\sin a}{a}}=1$$ і так само для sin b та sin c.

Доведення геометричне

Розглянемо сферу одиничного радіуса: $$OA=OB=OC=1$$

Будуємо точку $D$ та точку $E$ так, що $\angle ADO=\angle AEO=90^{\circ }$

Будуємо точку $A'$ так, що $\angle A'DO=\angle A'EO=90^{\circ }$

Тому видно, що $\angle ADA'=B$ та $\angle AEA'=C$

Точка $A'$ є проекцією точки $A$ на площину $OBC$. Тому $\angle AA'D=\angle AA'E=90^{\circ }$

Згідно з основною тригонометрією, маємо: $${\begin{aligned}AD&=\sin c\\AE&=\sin b\end{aligned}}$$

Але $AA'=AD\cdot \sin B=AE\cdot \sin C$

Поєднавши ці рівності, отримаємо: $${\begin{aligned}\sin c\cdot \sin B&=\sin b\cdot \sin C\\\Rightarrow {\frac {\sin B}{\sin b}}&={\frac {\sin C}{\sin c}}\end{aligned}}$$

Проводячи аналогічні обчислення, отримуємо теорему синусів для сферичного трикутника: $${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}$$

Малюнок, використаний в геометричному доказі вище, використовується і також надається в (див. Малюнок 3 у цьому документі) для виведення теореми синусів за допомогою елементарної лінійної алгебри та проекційних матриць.

Теорема синусів для гіперболічного трикутника

У гіперболічній геометрії з кривиною −1, теорема синусів для гіперболічного трикутника має вигляд:

$${\frac {\sin A}{\mathrm {sh} \,a}}={\frac {\sin B}{\mathrm {sh} \,b}}={\frac {\sin C}{\mathrm {sh} \,c}},$$

В окремому випадку, коли кут B прямий, отримаємо: $$\sin C={\frac {\sinh c}{\sinh b}}$$

що є аналогом формули в евклідовій геометрії, яка виражає синус кута як частку від ділення протилежної сторони прямокутного трикутника на його гіпотенузу.

Теорема синусів для поверхонь постійної кривини

Визначимо узагальнену функцію синусів, що залежить також від дійсного параметра K: $$\sin _{K}x=x-{\frac {Kx^{3}}{3!}}+{\frac {K^{2}x^{5}}{5!}}-{\frac {K^{3}x^{7}}{7!}}+\cdots .$$

Теорема синусів при постійній кривині K має вигляд $${\frac {\sin A}{\sin _{K}a}}={\frac {\sin B}{\sin _{K}b}}={\frac {\sin C}{\sin _{K}c}}\,.$$

Підставивши K = 0, K = 1, або K = −1, Отримаємо відповідно евклідовий, сферичний та гіперболічний випадки теореми синусів, описані вище.

Нехай p_K(r) позначає довжину кола радіуса r у просторі постійної кривини K.

Тоді p_K(r) = 2π sin_K r.

Тому теорему синусів також можна записати у вигляді: $${\frac {\sin A}{p_{K}(a)}}={\frac {\sin B}{p_{K}(b)}}={\frac {\sin C}{p_{K}(c)}}\,.$$

Це формулювання було знайдене Яношом Бояї.

У вищих розмірностях

• у тривімірному просторі тетраедр має чотири трикутних граней. Абсолютне значення полярних синусів (psin) нормальних векторів до трьох граней, що мають спільну вершину тетраедра, поділене на площу четвертої грані, не залежить від вибору вершини:

$${\begin{aligned}&{\frac {\left|\operatorname {psin} (\mathbf {b} ,\mathbf {c} ,\mathbf {d} )\right|}{\mathrm {S} _{a}}}={\frac {\left|\operatorname {psin} (\mathbf {a} ,\mathbf {c} ,\mathbf {d} )\right|}{\mathrm {S} _{b}}}={\frac {\left|\operatorname {psin} (\mathbf {a} ,\mathbf {b} ,\mathbf {d} )\right|}{\mathrm {S} _{c}}}={\frac {\left|\operatorname {psin} (\mathbf {a} ,\mathbf {b} ,\mathbf {c} )\right|}{\mathrm {S} _{d}}}\\[4pt]={}&{\frac {(3\operatorname {V} _{\text{тетр.}})^{2}}{2!~\mathrm {S} _{a}\cdot \mathrm {S} _{b}\cdot \mathrm {S} _{c}\cdot \mathrm {S} _{d}}}\,.\end{aligned}}$$

• Для n — вимірного симплекса (тобто, трикутника (n = 2), тетраедра (n = 3), п'ятикомірника (n = 4), тощо) в n — вимірному евклідовому просторі, абсолютна величина полярних синусів нормальних векторів до фасетів, що мають спільну вершину, поділена на гіперплощу грані, протилежної до цієї вершини, не залежить від вибору вершини.

Позначимо V — гіпероб'єм n-вимірного симплекса і P — добуток гіперплощ його (n - 1)-вимірних граней. Тоді загальне співвідношення має вигляд

$${\frac {\left|\operatorname {psin} (\mathbf {b} ,\ldots ,\mathbf {z} )\right|}{\mathrm {S} _{a}}}=\cdots ={\frac {\left|\operatorname {psin} (\mathbf {a} ,\ldots ,\mathbf {y} )\right|}{\mathrm {S} _{z}}}={\frac {(nV)^{n-1}}{(n-1)!P}}.$$

Історія

У першій главі Альмагеста (бл. 140 року н. е.) теорему синусів використано, але явно не сформульовано.

Найдавніше з доведень, що дійшли до нас, теореми синусів на площині описано в книзі Насир ад-Діна ат-Тусі «Трактат про повний чотирибічник» написаній у XIII столітті.

Теорему синусів для сферичного трикутника довели математики середньовічного Сходу ще в X столітті. У праці аль-Джайяні XI століття «Книга про невідомі дуги сфери» наводилось загальне доведення теореми синусів на сфері.

Див. також

• Тріангуляція
• Теорема косинусів
• Теорема тангенсів

Посилання

• Синусів теорема // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
• Теорема синусів: формулювання та доведення