Тернарна діаграма

Тернарна діаграма (тернарний графік, трикутна діаграма, симплексний графік, трикутник Гіббса або діаграма де Фінетті) — це барицентричний графік на трьох змінних, сума яких дорівнює константі.^[1] Він графічно зображує співвідношення трьох змінних у вигляді позицій у рівносторонньому трикутнику. Використовується у фізичній хімії, петрології, мінералогії, металургії та інших фізичних науках, щоб показати склад систем, що складаються з трьох основних компонентів. У популяційній генетиці трикутний графік частот генотипу називається діаграмою де Фінетті. У теорії ігор його часто називають симплексним графіком.^[2] Тернарні діаграми — це інструменти для аналізу композиційних даних у тривимірному випадку.

У тернарному графіку сума трьох змінних $a$ , $b$ і $c$ повинні дорівнювати деякій константі $K$ . Зазвичай ця константа представлена як 1,0 або 100 %. Оскільки $a + b + c = K$ для всіх речовин, які зображено на графіку, будь-яка змінна не є незалежною від інших, тому потрібно знати лише дві змінні, щоб знайти точку зразка на графіку: наприклад, $c$ має дорівнювати $K - a - b$ . Оскільки три числові значення не можуть змінюватися незалежно — існує лише два ступені вільності, — можна побудувати графіки комбінацій усіх трьох змінних лише у двох вимірах.

Перевага використання тернарного графіка для зображення хімічних складів полягає в тому, що три змінні можна зручно відобразити на двовимірному графіку. Потрійні діаграми також можна використовувати для створення фазових діаграм шляхом окреслення областей складу на діаграмі, де показані різні фази.

Значення точки на потрійному графіку відповідають (з точністю до константи) її трилінійним координатам або барицентричним координатам.

Зчитування значень на тернарному графіку

Існує три еквівалентні методи, які можна використовувати для визначення значень точки на графіку:

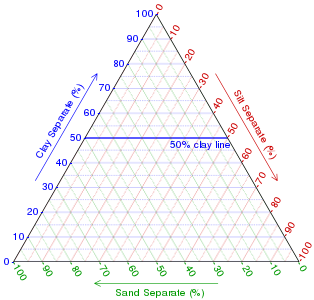
Метод паралельних ліній або метод сітки. Перший метод полягає у використанні сітки діаграми, що складається з ліній, паралельних ребрам трикутника. Паралель до сторони трикутника — геометричне місце точок, постійних у компоненті, позначеному при вершині, яка є протилежною цій стороні. Кожен компонент становить 100 % у вершині трикутника та 0 % на протилежному їй ребрі, зменшуючись лінійно зі збільшенням відстані (перпендикулярно до протилежного ребра) від цього кута. Проводячи паралельні лінії з рівними інтервалами між нульовою лінією та кутом, можна встановити точні поділки для легкої оцінки.
Метод перпендикулярних ліній або метод висот. Для діаграм, які не мають ліній сітки, найпростішим способом визначення значень є визначення найкоротших (тобто перпендикулярних) відстаней від точки інтересу до кожної з трьох сторін. Згідно з теоремою Вівіані, відстані (або відношення відстаней до висоти трикутника) дають значення кожного компонента.
Метод кутової лінії або метод перетину. Третій спосіб не вимагає малювання перпендикулярних або паралельних ліній. Прямі лінії проводяться від кожного кута через точку інтересу до протилежної сторони трикутника. Довжини цих ліній, а також довжини відрізків між точкою та відповідними сторонами вимірюють окремо. Тоді співвідношення виміряних ліній дає значення компонента у частках 100 %.

Переміщення вздовж паралельної прямої (лінії сітки) зберігає суму двох значень, тоді як переміщення вздовж перпендикулярної лінії збільшує (або зменшує) обидва значення на однакову величину, кожне вдвічі менше зменшення (збільшення) третього значення. Рух уздовж прямої через кут зберігає співвідношення двох інших величин.

Рисунок 1. Метод висот
Рисунок 2. Метод перетину
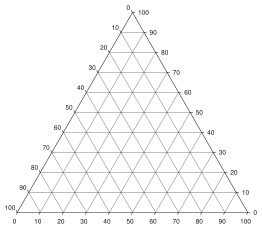
Рисунок 3. Приклад тернарної діаграми без нанесених точок.
Рисунок 4. Приклад тернарної діаграми, що показує прирости вздовж першої осі.
Рисунок 5. Приклад тернарної діаграми, що показує прирости вздовж другої осі.
Рисунок 6. Приклад тернарної діаграми, що показує прирости вздовж третьої осі.
Рисунок 7. Порожній тернарний графік
Рисунок 8. Позначення роботи трьох осей.
Трикутник без міток із основними лініями сітки
Трикутник без міток із основними та другорядними лініями сітки

Виведення з декартових координат

На рисунку (1) показана диметрична проекція точки $P(a, b, c)$ у тривимірному декартовому просторі з осями $a$ , $b$ і $c$ відповідно.

Якщо $a + b + c = K$ (додатна константа), $P$ обмежена площиною, яка містить $A(K,0,0)$ , $B(0, K,0)$ і $C(0,0, K)$ . Якщо $a$ , $b$ і $c$ не можуть бути від'ємними, $P$ обмежено трикутником, обмеженим $A$ , $B$ і $C$ , як у (2).

У (3) осі повертаються, щоб отримати ізометричний вигляд. Трикутник, дивлячись прямо на нього, виглядає рівностороннім.

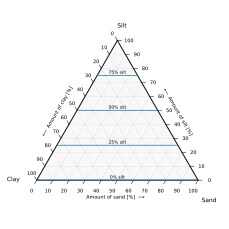
У (4) відстані $P$ від прямих $BC$ , $AC$ і $AB$ позначено $a'$ , $b'$ і $c'$ відповідно.

Для будь-якої прямої $l = s + t n̂$ у векторній формі ( $n̂$ — одиничний вектор) і точки $p$ , перпендикулярна відстань від $p$ до $l$ дорівнює

\left\|(\mathbf {s} -\mathbf {p} )-{\bigl (}(\mathbf {s} -\mathbf {p} )\cdot \mathbf {\hat {n}} {\bigr )}\mathbf {\hat {n}} \right\|\,.

У цьому випадку точка $P$ знаходиться в

\mathbf {p} ={\begin{pmatrix}a\\b\\c\end{pmatrix}}\,.

Лінія $BC$ має

\mathbf {s} ={\begin{pmatrix}0\\K\\0\end{pmatrix}}\quad {\text{and}}\quad \mathbf {\hat {n}} ={\frac {{\begin{pmatrix}0\\K\\0\end{pmatrix}}-{\begin{pmatrix}0\\0\\K\end{pmatrix}}}{\left\|{\begin{pmatrix}0\\K\\0\end{pmatrix}}-{\begin{pmatrix}0\\0\\K\end{pmatrix}}\right\|}}={\frac {\begin{pmatrix}0\\K\\-K\end{pmatrix}}{\sqrt {0^{2}+K^{2}+{(-K)}^{2}}}}={\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\,.

Використовуючи формулу перпендикулярної відстані,

{\begin{aligned}a'&=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left({\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}\cdot {\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]&=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left(0+{\frac {K-b}{\sqrt {2}}}+{\frac {c}{\sqrt {2}}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]&=\left\|{\begin{pmatrix}-a\\K-b-{\frac {K-b+c}{2}}\\-c+{\frac {K-b+c}{2}}\end{pmatrix}}\right\|=\left\|{\begin{pmatrix}-a\\{\frac {K-b-c}{2}}\\{\frac {K-b-c}{2}}\end{pmatrix}}\right\|\\[10px]&={\sqrt {{(-a)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}}}={\sqrt {a^{2}+{\frac {{(K-b-c)}^{2}}{2}}}}\,.\end{aligned}}

Підставляючи $K = a + b + c$ ,

a'={\sqrt {a^{2}+{\frac {{(a+b+c-b-c)}^{2}}{2}}}}={\sqrt {a^{2}+{\frac {a^{2}}{2}}}}=a{\sqrt {\frac {3}{2}}}\,.

Подібний розрахунок на прямих $AC$ і $AB$ дає

b'=b{\sqrt {\frac {3}{2}}}\quad {\text{and}}\quad c'=c{\sqrt {\frac {3}{2}}}\,.

Це показує, що відстань точки від відповідних ліній лінійно пропорційна вихідним значенням $a$ , $b$ і $c$ .^[3]

Побудова тернарної діаграми

Декартові координати корисні для нанесення точок у трикутнику. Розглянемо рівносторонній трикомпонентний графік, де $a = 100 %$ розміщено в $(x, y) = (0,0)$ і $b = 100 %$ в $(1,0)$ . Тоді $c = 100 %$ . ${\textstyle ({\frac {1}{2}},{\frac {\sqrt {3}}{2}}),}$ і трійка $(a, b, c)$ є

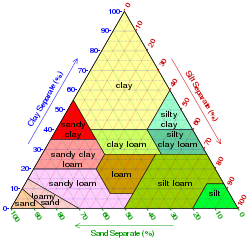
\left({\frac {1}{2}}\cdot {\frac {2b+c}{a+b+c}},{\frac {\sqrt {3}}{2}}\cdot {\frac {c}{a+b+c}}\right)\,.

Приклад

У цьому прикладі показано, як це працює для гіпотетичного набору з трьох зразків ґрунту:

Нанесення точок

Побудова зразка 1 (крок 1):

Знаходимо лінію вмісту 50% глини
Побудова зразка 1 (крок 2):

Знаходимо лінію вмісту 20% мулу
Побудова зразка 1 (крок 3):

Відповідно до перших двох кроків, перетин знаходиться на лінії вмісту 30% піску
Нанесення всіх трьох зразків
Тернарний графік типів ґрунтів за вмістом піску, глини та мулу, побудований за допомогою Mathematica

Приклади відомих тернарних діаграм

Див. також

Теорема Вівіані
Барицентричні координати
Композиційні дані
Трикутник управління проектами
Трилема
Симплексний метод планування експериментів

Примітки

↑ Weisstein, Eric W. Ternary Diagram. mathworld.wolfram.com (англ.). Процитовано 5 червня 2021.
↑ Karl Tuyls, «An evolutionary game-theoretic analysis of poker strategies», Entertainment Computing January 2009 DOI:10.1016/j.entcom.2009.09.002, p. 9
↑ Vaughan, Will (5 вересня 2010). Ternary plots. Архів оригіналу за 20 грудня 2010. Процитовано 7 вересня 2010.

Посилання

Excel Template for Ternary Diagrams. serc.carleton.edu. Science Education Resource Center (SERC) Carleton College. Процитовано 14 травня 2020.
Tri-plot: Ternary diagram plotting software. www.lboro.ac.uk. Loughborough University – Department of Geography / Resources Gateway home > Tri-plot. Процитовано 14 травня 2020.
Ternary Plot Generator – Quickly create ternary diagrams on line. www.ternaryplot.com. Процитовано 14 травня 2020.
Holland, Steven (2016). Data Analysis in the Geosciences – Ternary Diagrams developed in the R language. strata.uga.edu. University of Georgia. Процитовано 14 травня 2020.

[1] Weisstein, Eric W. Ternary Diagram. mathworld.wolfram.com (англ.). Процитовано 5 червня 2021.

[2] Karl Tuyls, «An evolutionary game-theoretic analysis of poker strategies», Entertainment Computing January 2009 DOI:10.1016/j.entcom.2009.09.002, p. 9

[Vaughan-3] Vaughan, Will (5 вересня 2010). Ternary plots. Архів оригіналу за 20 грудня 2010. Процитовано 7 вересня 2010.

[1]

[2]

[3]