Зоноедр

Гексоромбододекаедр — приклад зоноедра

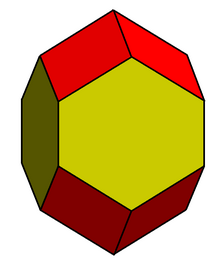
Зоноедр — многогранник, подаваний як сума Мінковського скінченного числа відрізків. Зоноедри в $n$-вимірному просторі називають також зонотопами.

Вперше визначив та дослідив Євграф Степанович Федоров.^{[джерело?]}

Двовимірний багатокутний аналог зоноедра називається зоногоном.

Властивості

• Зоноедр — опуклий многогранник, причому сам зоноедр і його грані всіх розмірностей центрально симетричні.
• Наявності центрів симетрії у всіх двовимірних граней опуклого многогранника досить, щоб він був зоноедром.
• Будь-який зоноедр є проєкцією куба досить високої розмірності.
• Будь-який зоноедр є центральним перетином октаедра досить високої розмірності.
• Будь-який зоноедр рівноскладений кубу.

Варіації та узагальнення

• У класі центрально симетричних опуклих тіл особливу роль грають зоноїди — тіла, граничні для зоноедрів. Вони допускають специфічне інтегральне подання опорної функції і є скінченновимірними перетинами кулі в банаховому просторіL¹.

Посилання

• «Зоопарк зоноедрів» [Архівовано 26 червня 2021 у Wayback Machine.] (англ.)