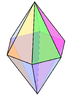
Трикутна біпіраміда
| Трикутна біпіраміда | |
|---|---|

| |
| Тип | Біпіраміда і правильногранний многогранник J11(M3+A5) — J12 (2M1) — J13(2M3) |
| Коксетер | |
| Шлефлі | {} + {3} |
| Список граней | 6 трикутників |
| Число ребер | 9 |
| Число вершин | 5 |
| Група симетрії | D3h, [3,2], (*223) порядку 12 |
| Група обертань | D3, [3,2]+, (223), порядку 6 |
| Тип грані | V3.4.4 |
| Двоїстий | трикутна призма |
| Властивості | опуклий, гранетранзитивний |
| Розгортка | 
|
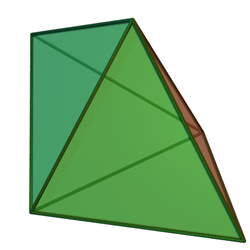
Трикутна біпіраміда — це вид шестигранника, перший многогранник у нескінченній послідовності гранетранзитивних біпірамід. Многогранник двоїстий трикутній призмі.
Як видно з назви, многогранник можна побудувати, з'єднавши два тетраедри однією гранню. Хоча всі грані многогранника конгруентні і тіло є ізоедричним, воно не є правильним многогранником, оскільки деякі вершини належать трьом граням, інші — чотирьом.
Біпіраміда, шість граней якої — правильні трикутники, є одним із правильногранних многогранників (J12 у нотації Джонсона, 2M1 у нотації Залгаллера). Правильногранний многогранник є одним з 92 строго опуклих многогранників, що мають правильні грані, але однорідним многогранником він не є (тобто не є правильним многогранником, архімедовим тілом, призмою чи антипризмою). Назву многограннику дав Норман Джонсон, який першим перерахував ці многогранники 1966 року[1]. Як правильногранний многогранник, грані якого — правильні трикутники, він є також дельтаедром.
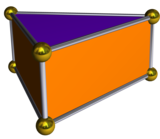
Подвійний многогранник трикутної біпіраміди — трикутна призма з п'ятьма гранями, два паралельні правильні трикутники, пов'язані ланцюжком з трьох прямокутників. Хоча трикутна призма має вид, що є однорідним многогранником (з квадратними гранями), двоїстий многогранник правильногранного виду біпіраміди має прямокутні грані, а не квадратні, так що многогранник не є однорідним.
| Двоїста трикутна біпіраміда | Розгортка двоїстого многогранника |
|---|---|
|

|
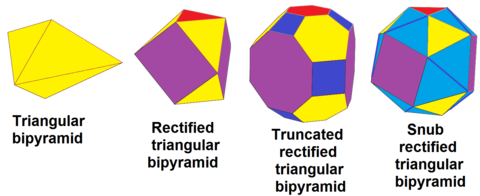
Трикутну біпіраміду dt{2,3} можна бачити в послідовності повнозрізаних многогранників, rdt{2,3}, зрізаних, trdt{2,3} і альтернованих (кирпатих) многогранників, srdt{2,3}:
Трикутну біпіраміду можна побудувати нарощуванням дрібніших частин, зокрема, з двох правильних октаедрів один над іншим з 3 трикутними біпірамідами, доданими навколо сторін і по 1 тетраедру зверху та знизу. Цей многогранник має 24 грані у вигляді правильних трикутників, але правильногранним многогранником він не є, оскільки має грані, розміщені в одній площині (копланарні грані). Цей многогранник є копланарним дельтаедром із 24 трикутними гранями. Він отримується нарощуванням комірок у скрученому альтернованому кубічному стільнику[en]. Великі трикутні многогранники можна отримати аналогічно з 9, 16 або 25 трикутниками на великій трикутній грані, що можна розглядати як частину трикутної мозаїки.
Трикутна біпіраміда може утворювати замощення простору з октаедрами або зрізаними тетраедрами[2].
 Шари однорідного четвертькубічного стільника[en] можна зсунути з утворенням пар тетраедричних комірок, які комбінуються в трикутні біпіраміди. Шари однорідного четвертькубічного стільника[en] можна зсунути з утворенням пар тетраедричних комірок, які комбінуються в трикутні біпіраміди.
|
 скручений тетраедричнооктаедричний стільник[en] має пари суміжних правильних тетраедрів, які можна розглядати як трикутні біпіраміди. скручений тетраедричнооктаедричний стільник[en] має пари суміжних правильних тетраедрів, які можна розглядати як трикутні біпіраміди.
|
| Багатогранник | 
|

|
|
|

|

|

|

| |
|---|---|---|---|---|---|---|---|---|---|
| Діаграма Коксетера — Динкіна | |||||||||
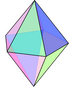
| Сферична мозаїка | 
|

|

|

|

|

|

|

|

|
| Конфігурація грані | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
- ↑ Johnson, 1966, с. 169–200.
- ↑ J12 honeycomb. Архів оригіналу за 16 березня 2018. Процитовано 6 березня 2018.
Norman D. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. — DOI:.
- Weisstein, Eric W. Трикутна біпіраміда(англ.) на сайті Wolfram MathWorld.
- Conway Notation for Polyhedra Try: dP3