Напівправильний многогранник

|

|

|

|

|

|

|

|

|

|

|

|

|
Напівправильні многогранники — низка опуклих многогранників, які не є правильними[1], але мають деякі їхні ознаки, серед яких однаковість усіх граней, всі грані є правильними многокутниками, просторова симетрія. Визначення може диференціюватися включаючи різні види многогранників, та в першу чергу сюди відносять архімедові тіла.
Архімедові тіла — опуклі многогранники, із двома властивостями:
- Всі грані є правильними многокутниками двох чи більше типів (якщо всі грані є правильними многокутниками одного типу, це — правильний многогранник);
- Для будь-якої пари вершин існує симетрія многогранника (рух що переводить многогранник в себе) що переводить одну вершину в іншу. Зокрема,
- Всі многогранні кути при вершинах конгруентні.
Історичні спогади приписують побудову перших напівправильних многогранників Архімеду, хоча доказових праць щодо обґрунтування ним принципів їх побудови не знайдено.
Тіла, двоїсті архімедовим, так звані каталанові тіла, мають конгруентні грані (переводяться одна в одну зсувом, обертанням або відбиттям), рівні двогранні кути та правильні многогранні кути. Каталанові тіла теж іноді називають напівправильними многогранниками. У цьому випадку напівправильними многогранниками вважають сукупність архімедових і каталанових тіл. Архімедові тіла є напівправильними многогранниками в тому сенсі, що їхні грані – правильні многокутники, але вони не однакові, а каталанові – в тому сенсі, що їхні грані однакові, але не є правильними многокутниками; при цьому для тих і тих зберігається умова одного з типів просторової симетрії: тетраедричного, октаедричного або ікосаедричного.
Тобто, напівправильними в цьому випадку називають тіла, в яких відсутня тільки одна з перших двох із таких властивостей правильних тіл:
- усі грані є правильними многокутниками ;
- усі грані однакові;
- тіло належить до одного з трьох типів просторової симетрії.
В архімедових тіл відсутня друга властивість, у каталанових - перша, третю властивість мають тіла обох видів.
Існує 13 архімедових тіл, два з яких (кирпатий куб і кирпатий додекаедр) не є дзеркально-симетричними і мають ліву та праву форми. Відповідно, існує 13 каталанових тіл.
| Многогранник — архімедове тіло | Грані | Вершини | Ребра | Конфігурація вершини | Двоїстий — каталанове тіло | Група симетрії |
|---|---|---|---|---|---|---|
 Кубооктаедр |
8 трикутників 6 квадратів |
12 | 24 | 3,4,3,4 |  Ромбододекаедр |
Oh |
 Ікосододекаедр |
20 трикутників 12 п'ятикутників |
30 | 60 | 3,5,3,5 |  |
Ih |
 Зрізаний тетраедр |
4 трикутники 4 шестикутники |
12 | 18 | 3,6,6 |  |
Td |
 Зрізаний октаедр |
6 квадратів 8 шестикутників |
24 | 36 | 4,6,6 |  (заломлёний куб) |
Oh |
 Зрізаний ікосаедр |
12 п'ятикуттників 20 шестикутників |
60 | 90 | 5,6,6 |  |
Ih |
 Зрізаний куб |
8 трикутників 6 восьмикутників |
24 | 36 | 3,8,8 |  |
Oh |
 Зрізаний додекаедр |
20 трикутників 12 десятикутників |
60 | 90 | 3,10,10 |  |
Ih |
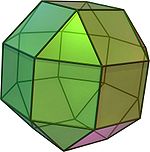 Ромбокубооктаедр |
8 трикутників 18 квадратів (6 — у кубічному положенні, 12 — у ромбічному) |
24 | 48 | 3,4,4,4 |  |
Oh |
 |
20 трикутників 30 квадратів 12 п'ятикутників |
60 | 120 | 3,4,5,4 |  |
Ih |
 |
12 квадратів 8 шестикутників 6 восьмикутників |
48 | 72 | 4,6,8 |  |
Oh |
 |
30 квадратів 20 шестикутників 12 десятикутників |
120 | 180 | 4,6,10 |  |
Ih |
  |
32 трикутники
|
24 | 60 | 3,3,3,3,4 | 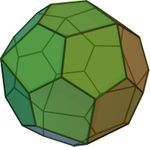  |
O |
  |
80 трикутників
|
60 | 150 | 3,3,3,3,5 |   |
I |
Крім архімедових і каталанових тіл, існують нескінченні послідовності многогранників, що належать до напівправильних: ті правильні призми та правильні антипризми, у яких усі ребра рівні.
Каталанові тіла - разом із платоновими тілами, рівногранними біпірамідами і трапецоедрами - використовують як гральні кісточки в деяких настільних іграх (див. світлини). Архімедові тіла, в яких грані не рівноправні і тому мають різні шанси випадання, для цього мало придатні.
- ↑ Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія 10-11 клас. — К. : Вежа, 2002. — С. 103. ISBN 966-7091-31-7.
- Гордєєва Є. П., Величко В. Л. Нарисна геометрія. багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007. — 198с.
- Ашкинузе В. Г. О числе полуправильных многогранников // Математическое просвещение. Вторая серия. — 1957. — Вип. 1 (14 грудня). — С. 107-118.
- Залгаллер В. А. Выпуклые многогранники с правильными гранями// Записки научных семинаров ЛОМИ. Том 2 -- 1966.
