Скалярний добуток

Скалярний добуток
Формула	${\boldsymbol {a}}\cdot {\boldsymbol {b}}=\sum _{i}a_{i}b_{i}$
Позначення у формулі	${\boldsymbol {a}}\cdot {\boldsymbol {b}}$, $a_{i}$, ${\boldsymbol {a}}$, ${\boldsymbol {b}}$ і $b_{i}$
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Скалярний добуток у Вікісховищі

Скаля́рний добу́ток (англ. dot product, scalar product) — бінарна операція над векторами, результатом якої є скаляр.

Скалярний добуток геометричних векторів ${\vec {x}}$ та ${\vec {y}}$ обчислюється за формулою:

${\vec {x}}\cdot {\vec {y}}=|{\vec {x}}|\,|{\vec {y}}|\,\cos \measuredangle \left({\vec {x}},{\vec {y}}\right)$

де $|{\vec {x}}|$ та $|{\vec {y}}|$ є довжинами векторів, а $\cos \measuredangle \left({\vec {x}},{\vec {y}}\right)$ дорівнює косинусу кута між цими векторами. Як і у випадку звичайного множення, знак множення можна не писати: ${\vec {x}}\cdot {\vec {y}}={\vec {x}}{\vec {y}}$.

Два означення добутку векторів:

• Скалярним добутком двох векторів називають число, рівне добутку довжин цих векторів на косинус кута між ними.
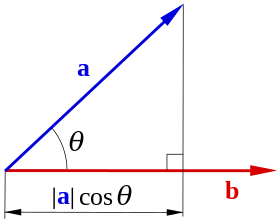
• Скалярним добутком двох векторів називають число, рівне добутку довжини одного з цих векторів на проєкцію іншого вектора на вісь, обумовлену першим з вказаних векторів (добуток довжини ${\vec {x}}$ на довжину проєкції ${\vec {y}}$ на ${\vec {x}}$).

В лінійній алгебрі поняття скалярного добутку узагальнено. Так, скалярним добутком називають функцію, що зіставляє парі елементів векторного простору елемент з поля, над яким побудований векторний простір. Скалярний добуток двох векторів $x$ та $y$ позначають як $\langle x,y\rangle$. Можлива і скорочена форма запису: $xy$. Також можливе позначення $x^{T}y$, що підкреслює зв'язок з множенням матриць.

Взагалі кажучи, для векторного простору існують різні варіанти скалярного добутку. Простір із визначеним скалярним добутком позначають як передгільбертів простір.

Визначення в евклідовому просторі

В лінійній алгебрі скалярний добуток двох векторів

${\vec {x}}={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}$    і   ${\vec {y}}={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}$

в ортонормованому базисі $n$-вимірного евклідового простору дорівнює сумі добутків координат векторів:

${\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}x_{i}y_{i}={x_{1}}{y_{1}}+{x_{2}}{y_{2}}+\dotsb +{x_{n}}{y_{n}}$.

В загальному випадку:

${\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}\sum _{j=1}^{n}x_{i}g_{ij}y_{j}={x_{1}}{y_{1}}+{x_{2}}{y_{2}}+\dotsb +{x_{n}}{y_{n}}$, де $g$ — елемент Матриці Грама

Наприклад, в тривимірному евклідовому просторі, скалярний добуток двох векторів обчислюється так:

${\begin{pmatrix}1&2&3\end{pmatrix}}\cdot {\begin{pmatrix}-7\\8\\9\end{pmatrix}}=1\cdot (-7)+2\cdot 8+3\cdot 9=36$,

тобто для того, щоб отримати значення скалярного добутку, матрицю-стовпчик, яка відповідає першому зі співмножників треба транспонувати й помножити на матрицю-стовпчик другого вектора за правилами множення матриць.

Норма векторів

Завдяки скалярному добутку, можна так обчислити норму вектора:

$||{\vec {x}}||={\sqrt {{\vec {x}}\cdot {\vec {x}}}}$.

Якщо простір евклідів, то:

$||{\vec {x}}||={\sqrt {{\vec {x}}\cdot {\vec {x}}}}={\sqrt {{x_{1}}^{2}+{x_{2}}^{2}+\dots +{x_{n}}^{2}}}$.

Обчислення кута

В евклідовому просторі виконується така рівність:

${\vec {x}}\cdot {\vec {y}}=|{\vec {x}}||{\vec {y}}|\cos \measuredangle \left({\vec {x}},{\vec {y}}\right)$.

На основі цього можна обчислити кут між векторами:

$\measuredangle \left({\vec {x}},{\vec {y}}\right)=\arccos {\frac {{\vec {x}}\cdot {\vec {y}}}{\left|{\vec {x}}\right|\,\left|{\vec {y}}\right|}}$.

Визначення стандартного скалярного добутку в просторі комплексних векторів

Для $\mathbb {C} ^{n}$ векторного простору над полем комплексних чисел стандартний скалярний добуток векторів ${\vec {x}},{\vec {y}}\in \mathbb {C} ^{n}$ визначається як відображення, що задовільняє наступним умовам:

${\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}x_{i}{\overline {y_{i}}}={x_{1}}{\overline {y_{1}}}+{x_{2}}{\overline {y_{2}}}+\dotsb +{x_{n}}{\overline {y_{n}}},$

де риска над комплексним числом позначає комплексно-спряжене число.

Інший варіант скалярного добутку можна визначити як

${\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}{\overline {x_{i}}}y_{i}={\overline {x_{1}}}{y_{1}}+{\overline {x_{2}}}{y_{2}}+\dotsb +{\overline {x_{n}}}{y_{n}}$.

Таке визначення здебільшого використовується в фізиці.

Результати обох визначень є взаємно-спряженими комплексними числами. Для скалярного добутку вектора на самого себе, який визначає норму вектора, обидва визначення дають однаковий результат.

Властивості

• Попри те, що у випадку дійсних чисел є симетричним, тобто ${\vec {x}}\cdot {\vec {y}}={\vec {y}}\cdot {\vec {x}}$, у випадку комплексних чисел є ермітовим, тобто ${\vec {x}}\cdot {\vec {y}}={\overline {{\vec {y}}\cdot {\vec {x}}}}$.
• Скалярний добуток не асоціативний (і не може бути, оскільки результатом скалярного добутку є скаляр, а не вектор).
• Скалярний добуток дистрибутивний стосовно додавання та віднімання.
• В евклідовому просторі спряженим стосовно лінійного оператора $A$ називається оператор $A^{*}$, для якого виконується рівність: $\langle A\cdot x,y\rangle =\langle x,A^{*}\cdot y\rangle$ для довільних $x$, $y$.

Узагальнене визначення

Якщо $L$ — лінійний простір над полем ${\mathcal {K}}$, а ${\overline {L}}$ — комплексно спряжений до $L$ то білінійне відображення $L\times L\to {\mathcal {K}}$, або, при ${\mathcal {K}}=\mathbb {C}$ відображення $L\times {\overline {L}}\to {\mathcal {K}}$ називається скалярним добутком.

• Скалярний добуток в дійсному векторному просторі $V$, це симетричне додатньовизначене білінійне відображення $\langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {R}$, тобто, для $x,y,z\in V$ та $\lambda \in \mathbb {R}$ виконуються такі умови:
  1. білінійність:
     • $\langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle$
     • $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$
     • $\langle x,\lambda y\rangle =\lambda \langle x,y\rangle =\langle \lambda x,y\rangle$
  2. симетричність: $\langle x,y\rangle =\langle y,x\rangle$
  3. додатньовизначеність: $\langle x,x\rangle \geq 0,$ та $\langle x,x\rangle =0$ якщо $x=0$
• Скалярний добуток в комплексному векторному просторі $V$, це ермітове додатньовизначене півторалінійне відображення $\langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {C}$, тобто, для $x,y,z\in V$ і $\lambda \in \mathbb {C}$ виконуються такі умови:
  1. півторалінійність:
     • $\langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle$
     • $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$
     • $\langle \lambda x,y\rangle =\lambda \langle x,y\rangle =\langle x,{\bar {\lambda }}y\rangle$
  2. ермітовість: $\langle x,y\rangle ={\overline {\langle y,x\rangle }}$
  3. додатньовизначеність: $\langle x,x\rangle \geq 0$ і $\langle x,x\rangle =0$, якщо $x=0$. (те, що $\langle x,x\rangle$ дійсний, витікає з умови 2)

Дійсний або комплексний векторний простір, в якому визначено скалярний добуток, називається прегільбертовим.

Представлення у вигляді добутку матриць

Стандартний скалярний добуток можна представити як добуток матриць. Водночас вектор представляється у вигляді матриці-стовпчика.

У випадку дійсних чисел, скалярний добуток представляється як:

$\langle x,y\rangle =x^{T}y=y^{T}x$,

де знаком ${}^{T}$ позначається транспонування матриці.

У випадку комплексних чисел виконується:

$\langle x,y\rangle =x^{*}y$,

де знаком ${}^{*}$ позначається ермітово-спряжена матриця.

Взагалі кажучи, у випадку дійсних чисел, кожна симетрична та додатноозначена матриця $A$ визначає скалярний добуток:

$\langle x,y\rangle _{A}=x^{T}Ay$;

аналогічно, у випадку комплексних чисел кожна ермітова додатноозначена матриця $A$ визначає скалярний добуток:

$\langle x,y\rangle _{A}=x^{*}Ay$.

Див. також

Ермітів скалярний добуток Векторний добуток Гільбертів простір

Норма (математика) Нерівність Коші — Буняковського

Джерела

• Гантмахер Ф. Р. Теорія матриць. — 2025. — 757 с.(укр.)
• Гельфанд І. М. Лекції з лінійної алгебри. — 2025. — 248 с.(укр.)
• Ахиезер Н.И., Глазман И.М. Теория линейных операторов в гильбертовом пространстве. — 3-є. — Х. : Вища школа, 1977. — Т. 1. — 316 с.(рос.)
• Добуток скалярний // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.