Число перетинів (теорія вузлів)

Трилисник без симетрії 3-го порядку з позначеними перетинами

Таблиця всіх простих вузлів з сімома або менше перетинами (дзеркальні варіанти не включено)

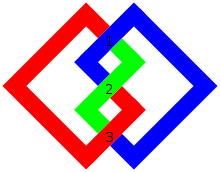
В теорії вузлів число перетинів вузла — це найменше число перетинів на будь-який з діаграм вузла. Число перетинів є інваріантом вузла.

Приклади

Як приклад: тривіальний вузол має нульове число перетинів, число перетинів трилисника дорівнює 3, а число перетинів вісімки дорівнює 4. Більше немає вузлів з числом перетинів 4 і менше, і є тільки два вузли з числом перетинів 5, але число вузлів з конкретними числами перетинів швидко зростає в міру зростання числа перетинів.

Таблиці

Таблиці простих вузлів традиційно індексуються числом перетинів з додатковим описом, який саме вузол зі множини вузлів із заданим числом перетинів мають на увазі (це впорядкування не базується на будь-яких властивостях, за винятком торичних вузлів, для яких скручені вузли перелічують першими). Список починається з 3₁ (трилисник), 4₁ (вісімка), 5₁ 5_2, 6_1, і так далі. Цей порядок істотно не змінився з часів Тейта, що опублікував таблицю 1877 року.

Адитивність

Є дуже малий прогрес у розумінні поведінки числа перетинів під час елементарних операцій на вузлах. Велике відкрите питання — чи є число перетинів адитивним відносно операції конкатенації. Також очікується, що сателітний вузол вузла K матиме більшу кількість перетинів, ніж K, але це не доведено.

Адитивність числа перетинів конкатенації вузлів доведена для особливих випадків, наприклад, якщо початкові вузли є альтернованими або якщо вихідні вузли є торическими. Марк Лакенбай довів, що існує константа N> 1, така що ${\frac {1}{N}}(\mathrm {cr} (K_{1})+\mathrm {cr} (K_{2}))\leq \mathrm {cr} (K_{1}+K_{2})$, але його метод, який використовує нормальні поверхні, не може поліпшити N до 1.

Застосування в біоінформатиці

Є дивний зв'язок між числом перетинів вузла і фізичною поведінкою вузлів ДНК. Для простих вузлів ДНК кількість перетинів є хорошим провісником відносної швидкості вузла ДНК електрофорезу гелю агарози. Переважно, більше число перетинів призводить до більшої відносної швидкості.

Пов'язані інваріанти

Є пов'язані поняття середнього числа перетинів і асимптотичного числа перетинів. Обидва ці поняття визначають границі стандартного числа перетинів. Є гіпотеза, що асимптотичне число перетинів дорівнює числу перетинів.

Іншими числовими інваріантами вузла є число мостів, коефіцієнт зачеплення, число відрізків і число розв'язування.

Література

• Simon Jonathan. Energy functions for knots: Beginning to predict physical behavior // Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. — 1996. — Т. 82. — (The IMA Volumes in Mathematics and its Applications). — DOI:10.1007/978-1-4612-4066-2_4.
• P. G. Tait. On Knots I, II, III // Scientific papers. — Cambridge University Press, 1898. — Т. 1.
• C. A. Adams. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. — American Mathematical Society, 2004. — ISBN 9780821836781.
• H. Gruber. Estimates for the minimal crossing number. — 2003. — arXiv:math/0303273.
• Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. — 2004. — Т. 13, вип. 7. — DOI:10.1142/S0218216504003524.
• Marc Lackenby. The crossing number of composite knots // Journal of Topology. — 2009. — Т. 2, вип. 4. — DOI:10.1112/jtopol/jtp028.