Стала Ейлера — Маскероні

Стала Ейлера — Маскероні
Названо на честь	Леонард Ейлер і Lorenzo Mascheronid
Першовідкривач або винахідник	Леонард Ейлер
Дата відкриття (винаходу)	1734
Позначення величини	γ
Числове значення	0,577215664902
Формула	$\gamma =\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln n\right)$
Позначення у формулі	$\gamma$ і $\ln x$
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Стала Ейлера — Маскероні у Вікісховищі

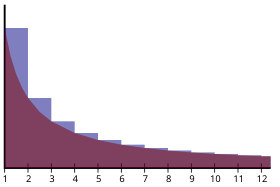
Площа синьої області збігається до сталої Ейлера.

Не плутати з числом Ейлера, ${\rm {e}}\approx 2{,}71828$, основою натурального логарифма.

Стала Ейлера (або Ейлера — Маскероні) — математична константа, яку позначають малою грецькою літерою гамма $\gamma$.

Вона визначається як границя різниці між гармонійним рядом і натуральним логарифмом, що позначається як $\ln$:

${\begin{aligned}\gamma &=\lim _{n\to +\infty }\left(-\ln n+\sum _{k=1}^{n}{\frac {1}{k}}\right)\\&=\int _{1}^{\infty }\left(-{\frac {1}{x}}+{\frac {1}{\lfloor x\rfloor }}\right){\rm {d}}x.\end{aligned}}$

Тут $\lfloor x\rfloor$ — ціла частина числа.

Числове значення сталої Ейлера з точністю до 50 знаків після коми:

$0{,}57721\,56649\,01532\,86060\,65120\,90082\,40243\,10421\,59335\,93992\,\dots .$

Історія

Константа вперше з'явилася в 1734 році в роботі швейцарського математика Леонарда Ейлера «De Progressionibus harmonicis observationes» (Eneström Index 43). Для константи Ейлер використовував позначення C та O. У 1790 році італійський математик Лоренцо Маскероні використав для константи позначення A та a. Позначення γ ніде не зустрічається в роботах ні Ейлера, ні Маскероні, і було обране пізніше, можливо, через зв'язок константи з гамма-функцією. Наприклад, німецький математик Карл Антон Бретшнайдер використовував позначення γ у 1835 році, а Август де Морган використовував його в підручнику, опублікованому частинами з 1836 по 1842 роки.

Застосування

Стала Ейлера, серед іншого, зустрічається ('*' означає, що відповідний елемент містить рівняння у явному вигляді), зокрема, в таких поняттях:

• співвідношення з експоненційним інтегралом*;
• перетворення Лапласа* для натурального логарифма;
• перший член розкладу в Ряд Лорана для Дзета-функції Рімана*, де вона є першою з констант Стілтьєса*;
• обчислення дигамма-функції;
• формула добутку для гамма-функції;
• асимптотичний розклад гамма-функції для малих аргументів;
• нерівність для функції Ейлера;
• швидкість зростання функції дільників;
• у регуляризації розмірності Діаграм Фейнмана в квантовій теорії поля;
• обчислення сталої Мейселя — Мертенса;
• третя теорема Мертенса*;
• розв'язок рівняння Бесселя другого роду;
• у регуляризації/перенормуванні гармонічного ряду як скінченне значення;
• математичне сподівання розподілу Гамбеля;
• інформаційна ентропія розподілів Вейбулла і Леві і, неявно, розподілу хі-квадрат для одного або двох степенів вільності;
• розв'язок задачі про збирача купонів*;
• у деяких формулюваннях закону Ципфа;
• означення інтегрального косинуса*;
• нижня межа щілини простих чисел;
• верхня межа ентропії Шеннона в квантовій теорії інформації;.
• модель Фішера—Орра для генетики адаптації в еволюційній біології;

Властивості

Не доведено чи є число $\gamma$ алгебраїчним або трансцендентним. Насправді навіть невідомо, чи є $\gamma$ ірраціональним. Використовуючи ланцюгові дроби, Папаніколау показав у 1997 році, що якщо $\gamma$ є раціональним, його знаменник повинен бути більшим за 10²⁴⁴⁶⁶³. Універсальність числа $\gamma$ підтверджується великою кількістю рівнянь нижче, що робить питання ірраціональності $\gamma$ є головним відкритим питанням у математиці.

Проте певний прогрес все ж досягнуто. Курт Малер показав у 1968 р., що число ${\dfrac {\pi Y_{0}(2)}{2J_{0}(2)}}-\gamma$ є трансцендентним (тут $J_{\alpha }(x)$ і $Y_{\alpha }(x)$ є функціями Бесселя. У 2009 році Олександр Аптекарев довів, що принаймні одна з констант Ейлера $\gamma$ або Ейлера — Гомперца $\delta$ є ірраціональною. Тангі Рівоаль довів у 2012 році, що принаймні одна з них є трансцендентною. У 2010 р. М. Рам Мурті та Н.Сарадха показали, що принаймі одне з чисел вигляду

$\gamma (a,q)=\lim _{n\to +\infty }\left(\left(\sum _{k=0}^{n}{\frac {1}{a+kq}}\right)-{\frac {\log(a+nq)}{q}}\right),$

де $q\geq 2$ і $1\leq a<q$, є алгебраїчним; це сімейство включає частинний випадок $\gamma (2,4)={\frac {\gamma }{4}}$. У 2013 році М. Рам Мурті та А. Зайцева знайшли іншу сім'ю, що містить $\gamma$, яке базується на сумах обернених цілих чисел, які не діляться на фіксований список простих чисел з однією і тією ж властивістю.

Зв'язок з гамма-функцією

$\gamma$ пов'язана з дигамма-функцією $\Psi$, а отже із похідною від гамма-функції, якщо обидві функції обчислювати в 1. Таким чином,

$-\gamma =\Gamma '(1)=\Psi (1).$

Це дорівнює границям:

${\begin{aligned}-\gamma &=\lim _{z\to 0}\left(\Gamma (z)-{\frac {1}{z}}\right)=\lim _{z\to 0}\left(\Psi (z)+{\frac {1}{z}}\right).\end{aligned}}$

Подальші обчислення границь:

${\begin{aligned}\lim _{z\to 0}{\frac {1}{z}}\left({\frac {1}{\Gamma (1+z)}}-{\frac {1}{\Gamma (1-z)}}\right)&=2\gamma \\\lim _{z\to 0}{\frac {1}{z}}\left({\frac {1}{\Psi (1-z)}}-{\frac {1}{\Psi (1+z)}}\right)&={\frac {\pi ^{2}}{3\gamma ^{2}}}.\end{aligned}}$

Границя пов'язана з бета-функцією (записана за допомогою гамма-функції):

${\begin{aligned}\gamma &=\lim _{n\to \infty }\left({\frac {\Gamma \left({\frac {1}{n}}\right)\Gamma (n+1)\,n^{1+{\frac {1}{n}}}}{\Gamma \left(2+n+{\frac {1}{n}}\right)}}-{\frac {n^{2}}{n+1}}\right)=\lim \limits _{m\to \infty }\sum _{k=1}^{m}{m \choose k}{\frac {(-1)^{k}}{k}}\log {\big (}\Gamma (k+1){\big )}.\end{aligned}}$

Зв'язок з дзета-функцією

$\gamma$ також можна виразити як нескінченну суму, члени якої включають дзета-функцію Рімана, яка обчислюється для цілих додатних числах:

${\begin{aligned}\gamma &=\sum _{m=2}^{\infty }(-1)^{m}{\frac {\zeta (m)}{m}}=\log {\frac {4}{\pi }}+\sum _{m=2}^{\infty }(-1)^{m}{\frac {\zeta (m)}{2^{m-1}m}}.\end{aligned}}$

Інші ряди, пов'язані з дзета-функцією, включають:

${\begin{aligned}\gamma &={\tfrac {3}{2}}-\log 2-\sum _{m=2}^{\infty }(-1)^{m}\,{\frac {m-1}{m}}{\big (}\zeta (m)-1{\big )}=\lim _{n\to \infty }\left({\frac {2n-1}{2n}}-\log n+\sum _{k=2}^{n}\left({\frac {1}{k}}-{\frac {\zeta (1-k)}{n^{k}}}\right)\right)=\\&=\lim _{n\to \infty }\left({\frac {2^{n}}{e^{2^{n}}}}\sum _{m=0}^{\infty }{\frac {2^{mn}}{(m+1)!}}\sum _{t=0}^{m}{\frac {1}{t+1}}-n\log 2+O\left({\frac {1}{2^{n}\,e^{2^{n}}}}\right)\right).\end{aligned}}$

Похибка в останньому рівнянні є швидкоспадною функцією змінної $n$. У результаті формула добре підходить для ефективного обчислення константи з високою точністю.

Іншими цікавими границями, що дорівнюють сталій Ейлера, є антисиметрична границя:

${\begin{aligned}\gamma &=\lim _{s\to 1^{+}}\sum _{n=1}^{\infty }\left({\frac {1}{n^{s}}}-{\frac {1}{s^{n}}}\right)=\lim _{s\to 1}\left(\zeta (s)-{\frac {1}{s-1}}\right)=\lim _{s\to 0}{\frac {\zeta (1+s)+\zeta (1-s)}{2}}\end{aligned}}$

і наступна формула, отримана в 1898 році де ла Валле-Пуссеном:

$\gamma =\lim _{n\to \infty }{\frac {1}{n}}\,\sum _{k=1}^{n}\left(\left\lceil {\frac {n}{k}}\right\rceil -{\frac {n}{k}}\right)$

де $\lceil \,\rceil$ функція стелі Ця формула вказує, що коли беремо будь-яке натуральне число $n$ і ділимо його на будь—яке натуральне число $k$ менше за $n$, то середня частка до якої спадає частка ${\frac {n}{k}}$ менша наступного цілого числа, прямує до $\gamma$ (ніж до $0{,}5$), якщо $n$ прямує до нескінченності.

З цим тісно пов'язане представлення у вигляді раціонального дзета-ряду. Взявши окремо декілька перших членів ряду наведеного вище, можна отримати оцінку для класичної границі ряду:

$\gamma =\sum _{k=1}^{n}{\frac {1}{k}}-\log n-\sum _{m=2}^{\infty }{\frac {\zeta (m,n+1)}{m}},$

де $\zeta (s,k)$ дзета-функція Гурвіца. Сума в цьому рівнянні включає гармонічні числа $H_{n}$. Розписавши деякі члени дзета-функції Гурвіца отримуємо:

$H_{n}=\log(n)+\gamma +{\frac {1}{2n}}-{\frac {1}{12n^{2}}}+{\frac {1}{120n^{4}}}-\varepsilon ,$

де $0<\varepsilon <{\dfrac {1}{252n^{6}}}$. $\gamma$ також можна представити наступним чином:

$\gamma =12\,\log(A)-\log(2\pi )+{\frac {6}{\pi ^{2}}}\,\zeta '(2)$

де $A$ стала Глейшера — Кінкеліна. $\gamma$ також можна представити у вигляді:

$\gamma =\lim _{n\to \infty }{\biggl (}-n+\zeta {\Bigl (}{\frac {n+1}{n}}{\Bigr )}{\biggr )}$

який отримується з розкладу дзета-функції у ряд Лорана.

Інтеграли

$\gamma$ дорівнює таким значенням визначених інтегралів:

${\begin{aligned}\gamma &=-\int _{0}^{\infty }e^{-x}\log x\,dx\quad =-\int _{0}^{1}\log \left(\log {\frac {1}{x}}\right)dx\quad =\int _{0}^{\infty }\left({\frac {1}{e^{x}-1}}-{\frac {1}{x\cdot e^{x}}}\right)dx=\\&=\int _{0}^{1}{\frac {1-e^{-x}}{x}}\,dx-\int _{1}^{\infty }{\frac {e^{-x}}{x}}\,dx\quad =\int _{0}^{1}\left({\frac {1}{\log x}}+{\frac {1}{1-x}}\right)dx=\\&=\int _{0}^{\infty }\left({\frac {1}{1+x^{k}}}-e^{-x}\right){\frac {dx}{x}},\quad k>0\\&=2\int _{0}^{\infty }{\frac {e^{-x^{2}}-e^{-x}}{x}}\,dx\quad =\int _{0}^{1}H_{x}\,dx,\end{aligned}}$

де $H_{x}$ дробове Гармонічне число. Третю формулу в інтегральному списку можна довести наступним чином:

${\begin{aligned}&\int _{0}^{\infty }\left({\frac {1}{e^{x}-1}}-{\frac {1}{xe^{x}}}\right)dx=\int _{0}^{\infty }{\frac {e^{-x}+x-1}{x[e^{x}-1]}}dx=\int _{0}^{\infty }{\frac {1}{x[e^{x}-1]}}\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}x^{m+1}}{(m+1)!}}dx\\[2pt]&=\int _{0}^{\infty }\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}x^{m}}{(m+1)![e^{x}-1]}}dx=\sum _{m=1}^{\infty }\int _{0}^{\infty }{\frac {(-1)^{m+1}x^{m}}{(m+1)![e^{x}-1]}}dx=\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}}{(m+1)!}}\int _{0}^{\infty }{\frac {x^{m}}{e^{x}-1}}dx\\[2pt]&=\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}}{(m+1)!}}m!\zeta (m+1)=\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}}{m+1}}\zeta (m+1)=\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}}{m+1}}\sum _{n=1}^{\infty }{\frac {1}{n^{m+1}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {(-1)^{m+1}}{m+1}}{\frac {1}{n^{m+1}}}\\[2pt]&=\sum _{n=1}^{\infty }\sum _{m=1}^{\infty }{\frac {(-1)^{m+1}}{m+1}}{\frac {1}{n^{m+1}}}=\sum _{n=1}^{\infty }\left[{\frac {1}{n}}-\ln \left(1+{\frac {1}{n}}\right)\right]=\gamma \end{aligned}}$

Інтеграл у третьому рядку— значення функції Дебая в $+\infty$, яке в свою чергу дорівнює $m!\zeta (m+1)$.

Визначені інтеграли, у яких зустрічається $\gamma$ :

${\begin{aligned}\int _{0}^{\infty }e^{-x^{2}}\log x\,dx&=-{\frac {(\gamma +2\log 2){\sqrt {\pi }}}{4}}\\\int _{0}^{\infty }e^{-x}\log ^{2}x\,dx&=\gamma ^{2}+{\frac {\pi ^{2}}{6}}\\\int _{-\infty }^{\infty }{\frac {e^{-|x|}\log |x|}{2}}\,dx&=\gamma \end{aligned}}$

Можна виразити $\gamma$, використовуючи частинний випадок формули Хаджикостаса як подвійний інтеграл з еквівалентним рядом:

${\begin{aligned}\gamma &=\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1-xy)\log xy}}\,dx\,dy=\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\log {\frac {n+1}{n}}\right).\end{aligned}}$

Цікавим є порівняння Сондоу:

${\begin{aligned}\log {\frac {4}{\pi }}&=\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1+xy)\log xy}}\,{\rm {d}}x\,{\rm {d}}y\\&=\sum _{n=1}^{\infty }\left((-1)^{n-1}\left({\frac {1}{n}}-\log {\frac {n+1}{n}}\right)\right).\end{aligned}}$

Це показує, що $\log {\frac {4}{\pi }}$ можна розглядати як «знакозмінну сталу Ейлера». Ці дві сталі також пов'язані за допомогою пари рядів

${\begin{aligned}\gamma &=\sum _{n=1}^{\infty }{\frac {N_{1}(n)+N_{0}(n)}{2n(2n+1)}}\\\log {\frac {4}{\pi }}&=\sum _{n=1}^{\infty }{\frac {N_{1}(n)-N_{0}(n)}{2n(2n+1)}},\end{aligned}}$

де $N_{1}(n)$ і $N_{0}(n)$— відповідно кількість одиниць і нулів у розкладі $n$ за основою 2. Також $\gamma$ можна записати за допомогою інтеграла Каталана

$\gamma =\int _{0}^{1}\left({\frac {1}{1+x}}\sum _{n=1}^{\infty }x^{2^{n}-1}\right)\,dx.$

Розклад в ряд

У загальному випадку

$\gamma =\lim _{n\to \infty }\left({\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+\ldots +{\frac {1}{n}}-\log(n+\alpha )\right)\equiv \lim _{n\to \infty }\gamma _{n}(\alpha )$

для будь-якого $\alpha >-n$. Однак швидкість збіжності цього розкладу значною мірою залежить від $\alpha$. Зокрема, $\gamma _{n}\left({\frac {1}{2}}\right)$ демонструє набагато швидшу збіжність, ніж стандартний розклад $\gamma _{n}(0)$. Це тому, що

${\frac {1}{2(n+1)}}<\gamma _{n}(0)-\gamma <{\frac {1}{2n}},$

коли

${\frac {1}{24(n+1)^{2}}}<\gamma _{n}(1/2)-\gamma <{\frac {1}{24n^{2}}}.$

Тим не менш, існують інші розклади рядів, які збігаються швидше, ніж цей; деякі з них розглянуті нижче.

Ейлер показав, що наступний нескінченний ряд збігається до $\gamma$:

$\gamma =\sum _{k=1}^{\infty }\left({\frac {1}{k}}-\log \left(1+{\frac {1}{k}}\right)\right).$

Цей ряд для $\gamma$ еквівалентний ряду Нільсена, знайденому в 1897 році:

$\gamma =1-\sum _{k=2}^{\infty }(-1)^{k}{\frac {\left\lfloor \log _{2}k\right\rfloor }{k+1}}.$

У 1810 році Вакка знайшов тісно пов'язаний ряд

${\begin{aligned}\gamma &=\sum _{k=2}^{\infty }(-1)^{k}{\frac {\left\lfloor \log _{2}k\right\rfloor }{k}}\\[5pt]&={\tfrac {1}{2}}-{\tfrac {1}{3}}+2\left({\tfrac {1}{4}}-{\tfrac {1}{5}}+{\tfrac {1}{6}}-{\tfrac {1}{7}}\right)+3\left({\tfrac {1}{8}}-{\tfrac {1}{9}}+{\tfrac {1}{10}}-{\tfrac {1}{11}}+\cdots -{\tfrac {1}{15}}\right)+\cdots ,\end{aligned}}$

де $\log _{2}$ — це логарифм за основою 2, $\lfloor ~\rfloor$ — функція підлоги.

У 1926 році він знайшов інший ряд:

${\begin{aligned}\gamma +\zeta (2)&=\sum _{k=2}^{\infty }\left({\frac {1}{\left\lfloor {\sqrt {k}}\right\rfloor ^{2}}}-{\frac {1}{k}}\right)\\[5pt]&=\sum _{k=2}^{\infty }{\frac {k-\left\lfloor {\sqrt {k}}\right\rfloor ^{2}}{k\left\lfloor {\sqrt {k}}\right\rfloor ^{2}}}\\[5pt]&={\frac {1}{2}}+{\frac {2}{3}}+{\frac {1}{2^{2}}}\sum _{k=1}^{2\cdot 2}{\frac {k}{k+2^{2}}}+{\frac {1}{3^{2}}}\sum _{k=1}^{3\cdot 2}{\frac {k}{k+3^{2}}}+\cdots \end{aligned}}$

Із розкладу в ряд Мальстена—Куммера для логарифма гамма-функціїотримуємо

$\gamma =\log \pi -4\log \left(\Gamma ({\tfrac {3}{4}})\right)+{\frac {4}{\pi }}\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {\log(2k+1)}{2k+1}}.$

Важливий розклад у ряд сталої Ейлера отримали Фонтаною і Маскероні:

$\gamma =\sum _{n=1}^{\infty }{\frac {|G_{n}|}{n}}={\frac {1}{2}}+{\frac {1}{24}}+{\frac {1}{72}}+{\frac {19}{2880}}+{\frac {3}{800}}+\cdots ,$

де $G_{n}$— коефіцієнти Грегорі. Цей ряд є частинним випадком (при $k=1$) наступного розкладів:

${\begin{aligned}\gamma &=H_{k-1}-\log k+\sum _{n=1}^{\infty }{\frac {(n-1)!|G_{n}|}{k(k+1)\cdots (k+n-1)}}&&\\&=H_{k-1}-\log k+{\frac {1}{2k}}+{\frac {1}{12k(k+1)}}+{\frac {1}{12k(k+1)(k+2)}}+{\frac {19}{120k(k+1)(k+2)(k+3)}}+\cdots &&\end{aligned}}$

які є збіжними при.

Аналогічний ряд записаний з використанням чисел Коші другого роду $C_{n}$ має вигляд:

$\gamma =1-\sum _{n=1}^{\infty }{\frac {C_{n}}{n\,(n+1)!}}=1-{\frac {1}{4}}-{\frac {5}{72}}-{\frac {1}{32}}-{\frac {251}{14400}}-{\frac {19}{1728}}-\ldots$

Благоучин (2018) знайшов цікаве узагальнення ряду Фонтана—Машероні

$\gamma =\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{2n}}{\Big \{}\psi _{n}(a)+\psi _{n}{\Big (}-{\frac {a}{1+a}}{\Big )}{\Big \}},\quad a>-1$

де $\psi _{n}(a)$ — многочлени Бернуллі другого роду, які визначаються твірною функцією

${\frac {z(1+z)^{s}}{\log(1+z)}}=\sum _{n=0}^{\infty }z^{n}\psi _{n}(s),\qquad |z|<1,$

Для будь-якого раціонального $a$ цей ряд містить лише раціональні доданки. Наприклад, при $a=1$ маємо

$\gamma ={\frac {3}{4}}-{\frac {11}{96}}-{\frac {1}{72}}-{\frac {311}{46080}}-{\frac {5}{1152}}-{\frac {7291}{2322432}}-{\frac {243}{100352}}-\ldots$

Інші ряди з такими ж многочленами включають такі приклади:

$\gamma =-\log(a+1)-\sum _{n=1}^{\infty }{\frac {(-1)^{n}\psi _{n}(a)}{n}},\qquad \Re (a)>-1$

та

$\gamma =-{\frac {2}{1+2a}}\left\{\log \Gamma (a+1)-{\frac {1}{2}}\log(2\pi )+{\frac {1}{2}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}\psi _{n+1}(a)}{n}}\right\},\qquad \Re (a)>-1$

де $\Gamma (a)$ — гамма-функція. Ряд, пов'язаний з алгоритмом Акіяма—Танігави, має вигляд

$\gamma =\log(2\pi )-2-2\sum _{n=1}^{\infty }{\frac {(-1)^{n}G_{n}(2)}{n}}=\log(2\pi )-2+{\frac {2}{3}}+{\frac {1}{24}}+{\frac {7}{540}}+{\frac {17}{2880}}+{\frac {41}{12600}}+\ldots$

де $G_{n}(2)$ — коефіцієнти Грегорі другого порядку

Ряд простих чисел:

$\gamma =\lim _{n\to \infty }\left(\log n-\sum _{p\leq n}{\frac {\log p}{p-1}}\right).$

Асимптотичні розклади

$\gamma$ можна визначити за допомогою наступних асимптотичних формул (де $H_{n}$—$n$-е гармонічне число):

$\gamma \sim H_{n}-\log n-{\frac {1}{2n}}+{\frac {1}{12n^{2}}}-{\frac {1}{120n^{4}}}+\cdots$ (Ейлер)

$\gamma \sim H_{n}-\log \left({n+{\frac {1}{2}}+{\frac {1}{24n}}-{\frac {1}{48n^{2}}}+\cdots }\right)$ (Негой)

$\gamma \sim H_{n}-{\frac {\log n+\log(n+1)}{2}}-{\frac {1}{6n(n+1)}}+{\frac {1}{30n^{2}(n+1)^{2}}}-\cdots$ (Ернесто)

Третя формула також називається розкладом Рамануджана.

Алабдулмохсін отримав у замкненій формі співвідношення для сум похибок цих наближень. Він показав, що (теорема A.1): $$\sum _{n=1}^{\infty }\log n+\gamma -H_{n}+{\frac {1}{2n}}={\frac {\log(2\pi )-1-\gamma }{2}}$$ $$\sum _{n=1}^{\infty }\log {\sqrt {n(n+1)}}+\gamma -H_{n}={\frac {\log(2\pi )-1}{2}}-\gamma$$ $$\sum _{n=1}^{\infty }(-1)^{n}{\Big (}\log n+\gamma -H_{n}{\Big )}={\frac {\log \pi -\gamma }{2}}$$

Експонента

Стала ${\rm {{e}^{\gamma }}}$ є важливою в теорії чисел. Деякі автори позначають цю величину просто як $\gamma '$. ${\rm {{e}^{\gamma }}}$ дорівнює наступній границі, де $p_{n}$— $n$-е просте число:

$e^{\gamma }=\lim _{n\to \infty }{\frac {1}{\log p_{n}}}\prod _{i=1}^{n}{\frac {p_{i}}{p_{i}-1}}.$

Це підтверджує третю теорему Мертенса.. Числове значення ${\rm {{e}^{\gamma }}}$:

1.78107241799019798523650410310717954916964521430343....

Інші нескінченні добутки, що пов'язані з ${\rm {e}}^{\gamma }$, включають:

${\begin{aligned}{\frac {e^{1+{\frac {\gamma }{2}}}}{\sqrt {2\pi }}}&=\prod _{n=1}^{\infty }e^{-1+{\frac {1}{2n}}}\left(1+{\frac {1}{n}}\right)^{n}\\{\frac {e^{3+2\gamma }}{2\pi }}&=\prod _{n=1}^{\infty }e^{-2+{\frac {2}{n}}}\left(1+{\frac {2}{n}}\right)^{n}.\end{aligned}}$

Ці доданки є результатом G-функції Барнса.

Додатково

$e^{\gamma }={\sqrt {\frac {2}{1}}}\cdot {\sqrt[{3}]{\frac {2^{2}}{1\cdot 3}}}\cdot {\sqrt[{4}]{\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}}\cdot {\sqrt[{5}]{\frac {2^{4}\cdot 4^{4}}{1\cdot 3^{6}\cdot 5}}}\cdots$

де $n$-й множник — це $(n+1)$-й корінь з

$\prod _{k=0}^{n}(k+1)^{(-1)^{k+1}{n \choose k}}.$

Цей нескінченний добуток, вперше відкритий Сером у 1926 році, був перевідкритий Сонду за допомогою гіпергеометричних функцій. Також справедлива наступна формула:

${\frac {e^{\frac {\pi }{2}}+e^{-{\frac {\pi }{2}}}}{\pi e^{\gamma }}}=\prod _{n=1}^{\infty }\left(e^{-{\frac {1}{n}}}\left(1+{\frac {1}{n}}+{\frac {1}{2n^{2}}}\right)\right).$

Ланцюговий дріб

Розклад ланцюгового дробу для сталої $\gamma$ починається з $[0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,\dots ]$, і немає видимої закономірності. Відомо, що цей ланцюговий дріб має щонайменше 475 006 доданків і має нескінченно багато доданків тоді й лише тоді, коли стала є ірраціональним числом.

Узагальнення

abm(x) = γ_−x

Узагальнені сталі Ейлера визначаються як

$\gamma _{\alpha }=\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {1}{k^{\alpha }}}-\int _{1}^{n}{\frac {1}{x^{\alpha }}}\,dx\right),$

для $0<\alpha <1$, де $\gamma$ є особливим випадком при $\alpha =1$. Подальші узагальнення мають вигляд

$c_{f}=\lim _{n\to \infty }\left(\sum _{k=1}^{n}f(k)-\int _{1}^{n}f(x)\,dx\right)$

для деякої довільної спадної функції $f$. Наприклад,

$f_{n}(x)={\frac {(\log x)^{n}}{x}}$

приводить до констант Стілтьєса, а

$f_{a}(x)=x^{-a}$

дає

$\gamma _{f_{a}}={\frac {(a-1)\zeta (a)-1}{a-1}}$

де знову з'являється границя

$\gamma =\lim _{a\to 1}\left(\zeta (a)-{\frac {1}{a-1}}\right)$

Двовимірним граничним узагальненням є константа Массера — Гремена.

Сталі Ейлера — Лемера визначаються шляхом підсумовування обернених чисел у загальному класі за модулем:

$\gamma (a,q)=\lim _{x\to \infty }\left(\sum _{0<n\leq x \atop n\equiv a{\pmod {q}}}{\frac {1}{n}}-{\frac {\log x}{q}}\right).$

Основними властивостями яких є

${\begin{aligned}\gamma (0,q)&={\frac {\gamma -\log q}{q}},\\\sum _{a=0}^{q-1}\gamma (a,q)&=\gamma ,\\q\gamma (a,q)&=\gamma -\sum _{j=1}^{q-1}e^{-{\frac {2\pi aij}{q}}}\log \left(1-e^{\frac {2\pi ij}{q}}\right),\end{aligned}}$

і якщо, то

$q\gamma (a,q)={\frac {q}{d}}\gamma \left({\frac {a}{d}},{\frac {q}{d}}\right)-\log d.$

Опубліковані десяткові розклади для $\gamma$

Спочатку Ейлер обчислив значення константи з точністю до 6 знаків після коми. У 1781 році він обчислив його до 16 знаків після коми. Маскероні спробував обчислити константу з точністю до 32 знаків після коми, але допустив помилку в 20-22 і 31-32 знаках після коми; починаючи з 20-ї цифри, він обчислив $\dots 1811209008239$, хоча правильне значення дорівнює $\dots 0651209008240$.

Published Decimal Expansions of γ

Date	Decimal digits	Author	Sources
1734	5	Леонард Ейлер
1735	15	Леонард Ейлер
1781	16	Леонард Ейлер
1790	32	Лоренцо Маскероні, 20-22 і 31-32 неправильні
1809	22	Йоганн Георг фон Зольднер
1811	22	Карл Фрідріх Гаусс
1812	40	Фрідріх Бернхард Готфрід Ніколай
1857	34	Крістіан Фредрік Ліндман
1861	41	Людвіг Оттінгер
1867	49	Вільям Шенкс
1871	99	Джон Кауч Адамс
1871	101	Вільям Шенкс
1877	262	Джон Кауч Адамс
1952	328	Джон Ренч
1961	1050	Гельмут Фішер і Карл Целлер
1962	1271	Дональд Кнут
1962	3566	Дура В. Суїні
1973	4879	Вільям А. Бейєр і Майкл С. Уотерман
1977	20700	Річард П. Брент
1980	30100	Річард П. Брент і Едвін М. Макміллан
1993	172000	Джонатан Борвейн
1999	108000000	Патрік Демішель і Ксав'є Гурдон
March 13, 2009	29844489545	Олександр Дж. Йі та Реймонд Чан
December 22, 2013	119377958182	Олександр Дж.
March 15, 2016	160000000000	Пітер Труб
May 18, 2016	250000000000	Рон Уоткінс
August 23, 2017	477511832674	Рон Уоткінс
May 26, 2020	600000000100	Кім Синмін і Ян Катресс

Література

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)
• Bretschneider, Carl Anton (1837) [1835]. «Theoriae logarithmi integralis lineamenta nova». Crelle's Journal (in Latin). 17: 257—285.
• Ram Murty, M.; Saradha, N. (2010). «Euler—Lehmer constants and a conjecture of Erdos». Journal of Number Theory. 130 (12): 2671—2681. doi:10.1016/j.jnt.2010.07.004. ISSN 0022-314X.

Додаткова література

• Borwein, Jonathan M.; David M. Bradley; Richard E. Crandall (2000). Computational Strategies for the Riemann Zeta Function (PDF). Journal of Computational and Applied Mathematics. 121 (1–2): 11. Bibcode:2000JCoAM.121..247B. doi:10.1016/s0377-0427(00)00336-8. Derives γ as sums over Riemann zeta functions.
• Gerst, I. (1969). Some series for Euler's constant. Amer. Math. Monthly. 76 (3): 237—275. doi:10.2307/2316370. JSTOR 2316370.
• Glaisher, James Whitbread Lee (1872). On the history of Euler's constant. Messenger of Mathematics. 1: 25—30. JFM 03.0130.01.
• Gourdon, Xavier; Sebah, P. (2002). Collection of formulae for Euler's constant, γ.
• Gourdon, Xavier; Sebah, P. (2004). The Euler constant: γ.
• Karatsuba, E. A. (1991). Fast evaluation of transcendental functions. Probl. Inf. Transm. 27 (44): 339—360.
• Karatsuba, E.A. (2000). On the computation of the Euler constant γ. Journal of Numerical Algorithms. 24 (1–2): 83—97. doi:10.1023/A:1019137125281. S2CID 21545868.
• Knuth, Donald (1997). The Art of Computer Programming, Vol. 1 (вид. 3rd). Addison-Wesley. с. 75, 107, 114, 619—620. ISBN 0-201-89683-4.
• Lehmer, D. H. (1975). Euler constants for arithmetical progressions (PDF). Acta Arith. 27 (1): 125—142. doi:10.4064/aa-27-1-125-142.
• Lerch, M. (1897). Expressions nouvelles de la constante d'Euler. Sitzungsberichte der Königlich Böhmischen Gesellschaft der Wissenschaften. 42: 5.
• Mascheroni, Lorenzo (1790), Adnotationes ad calculum integralem Euleri, in quibus nonnulla problemata ab Eulero proposita resolvuntur, Galeati, Ticini
• Sondow, Jonathan (2002). A hypergeometric approach, via linear forms involving logarithms, to irrationality criteria for Euler's constant. Mathematica Slovaca. 59: 307—314. arXiv:math.NT/0211075. Bibcode:2002math.....11075S. doi:10.2478/s12175-009-0127-2. S2CID 16340929. with an Appendix by Sergey Zlobin

Зовнішні лінки

• Hazewinkel, Michiel, ред. (2001), constant Euler constant, Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
• Weisstein, Eric W. Euler–Mascheroni constant(англ.) на сайті Wolfram MathWorld.
• Jonathan Sondow.
• Fast Algorithms and the FEE Method, E.A. Karatsuba (2005)
• Further formulae which make use of the constant: Gourdon and Sebah (2004).

Див. також

• Формула сумування Абеля