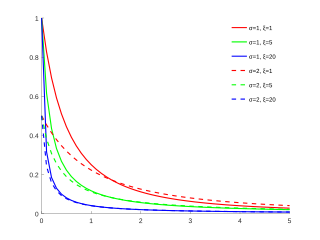
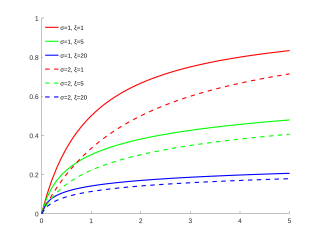
Узагальнений розподіл Парето
Функція розподілу УРП для
μ
=
0
{\displaystyle \mu =0}
і різних значень
σ
{\displaystyle \sigma }
та
ξ
{\displaystyle \xi }
Функція розподілу ймовірностей
Параметри
μ
∈
(
−
∞
,
∞
)
{\displaystyle \mu \in (-\infty ,\infty )\,}
зсув (дійсний )
σ
∈
(
0
,
∞
)
{\displaystyle \sigma \in (0,\infty )\,}
масштаб (дійсний)
ξ
∈
(
−
∞
,
∞
)
{\displaystyle \xi \in (-\infty ,\infty )\,}
форми (дійсний)Носій функції
x
⩾
μ
(
ξ
⩾
0
)
{\displaystyle x\geqslant \mu \,\;(\xi \geqslant 0)}
μ
⩽
x
⩽
μ
−
σ
/
ξ
(
ξ
<
0
)
{\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi \,\;(\xi <0)}
Розподіл імовірностей
1
σ
(
1
+
ξ
z
)
−
(
1
/
ξ
+
1
)
{\displaystyle {\frac {1}{\sigma }}(1+\xi z)^{-(1/\xi +1)}}
z
=
x
−
μ
σ
{\displaystyle z={\frac {x-\mu }{\sigma }}}
Функція розподілу ймовірностей (cdf)
1
−
(
1
+
ξ
z
)
−
1
/
ξ
{\displaystyle 1-(1+\xi z)^{-1/\xi }\,}
Середнє
μ
+
σ
1
−
ξ
(
ξ
<
1
)
{\displaystyle \mu +{\frac {\sigma }{1-\xi }}\,\;(\xi <1)}
Медіана
μ
+
σ
(
2
ξ
−
1
)
ξ
{\displaystyle \mu +{\frac {\sigma (2^{\xi }-1)}{\xi }}}
Мода
{\displaystyle }
Дисперсія
σ
2
(
1
−
ξ
)
2
(
1
−
2
ξ
)
(
ξ
<
1
/
2
)
{\displaystyle {\frac {\sigma ^{2}}{(1-\xi )^{2}(1-2\xi )}}\,\;(\xi <1/2)}
Коефіцієнт асиметрії
2
(
1
+
ξ
)
1
−
2
ξ
(
1
−
3
ξ
)
(
ξ
<
1
/
3
)
{\displaystyle {\frac {2(1+\xi ){\sqrt {1-2\xi }}}{(1-3\xi )}}\,\;(\xi <1/3)}
Коефіцієнт ексцесу
3
(
1
−
2
ξ
)
(
2
ξ
2
+
ξ
+
3
)
(
1
−
3
ξ
)
(
1
−
4
ξ
)
−
3
(
ξ
<
1
/
4
)
{\displaystyle {\frac {3(1-2\xi )(2\xi ^{2}+\xi +3)}{(1-3\xi )(1-4\xi )}}-3\,\;(\xi <1/4)}
Ентропія
log
(
σ
)
+
ξ
+
1
{\displaystyle \log(\sigma )+\xi +1}
Твірна функція моментів (mgf)
e
θ
μ
∑
j
=
0
∞
[
(
θ
σ
)
j
∏
k
=
0
j
(
1
−
k
ξ
)
]
,
(
k
ξ
<
1
)
{\displaystyle e^{\theta \mu }\,\sum _{j=0}^{\infty }\left[{\frac {(\theta \sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <1)}
Характеристична функція {{{char}}}
У статистиці , в узагальнений розподіл Парето (УРП, англ. Generalized Pareto distribution ) — це сімейство неперервних імовірнісних розподілів . Він часто використовується для моделювання хвостів інших розподілів. Він визначається трьома параметрами: параметром розташування
μ
{\displaystyle \mu }
σ
{\displaystyle \sigma }
ξ
{\displaystyle \xi }
[ 1] [ 2] [ 3]
κ
=
−
ξ
{\displaystyle \kappa =-\xi \,}
[ 4]
Стандартна функція розподілу УРП записується[ 5]
F
ξ
(
z
)
=
{
1
−
(
1
+
ξ
z
)
−
1
/
ξ
for
ξ
≠
0
,
1
−
e
−
z
for
ξ
=
0.
{\displaystyle F_{\xi }(z)={\begin{cases}1-\left(1+\xi z\right)^{-1/\xi }&{\text{for }}\xi \neq 0,\\1-e^{-z}&{\text{for }}\xi =0.\end{cases}}}
де носій
z
≥
0
{\displaystyle z\geq 0}
ξ
≥
0
{\displaystyle \xi \geq 0}
0
≤
z
≤
−
1
/
ξ
{\displaystyle 0\leq z\leq -1/\xi }
ξ
<
0
{\displaystyle \xi <0}
f
ξ
(
z
)
=
{
(
ξ
z
+
1
)
−
ξ
+
1
ξ
for
ξ
≠
0
,
e
−
z
for
ξ
=
0.
{\displaystyle f_{\xi }(z)={\begin{cases}(\xi z+1)^{-{\frac {\xi +1}{\xi }}}&{\text{for }}\xi \neq 0,\\e^{-z}&{\text{for }}\xi =0.\end{cases}}}
Пов'язані місцевості-масштаб сімейство розподілів, отриманих шляхом заміни аргументу Z з допомогою
x
−
μ
σ
{\displaystyle {\frac {x-\mu }{\sigma }}}
кумулятивна функція розподілу це
F
(
ξ
,
μ
,
σ
)
(
x
)
=
{
1
−
(
1
+
ξ
(
x
−
μ
)
σ
)
−
1
/
ξ
for
ξ
≠
0
,
1
−
exp
(
−
x
−
μ
σ
)
for
ξ
=
0.
{\displaystyle F_{(\xi ,\mu ,\sigma )}(x)={\begin{cases}1-\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }&{\text{for }}\xi \neq 0,\\1-\exp \left(-{\frac {x-\mu }{\sigma }}\right)&{\text{for }}\xi =0.\end{cases}}}
для
x
⩾
μ
{\displaystyle x\geqslant \mu }
ξ
⩾
0
{\displaystyle \xi \geqslant 0\,}
μ
⩽
x
⩽
μ
−
σ
/
ξ
{\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }
ξ
<
0
{\displaystyle \xi <0}
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
σ
>
0
{\displaystyle \sigma >0}
ξ
∈
R
{\displaystyle \xi \in \mathbb {R} }
Функції щільності :
f
(
ξ
,
μ
,
σ
)
(
x
)
=
1
σ
(
1
+
ξ
(
x
−
μ
)
σ
)
(
−
1
ξ
−
1
)
{\displaystyle f_{(\xi ,\mu ,\sigma )}(x)={\frac {1}{\sigma }}\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{\left(-{\frac {1}{\xi }}-1\right)}}
або еквівалентно
f
(
ξ
,
μ
,
σ
)
(
x
)
=
σ
1
ξ
(
σ
+
ξ
(
x
−
μ
)
)
1
ξ
+
1
{\displaystyle f_{(\xi ,\mu ,\sigma )}(x)={\frac {\sigma ^{\frac {1}{\xi }}}{\left(\sigma +\xi (x-\mu )\right)^{{\frac {1}{\xi }}+1}}}}
знову, для
x
⩾
μ
{\displaystyle x\geqslant \mu }
ξ
⩾
0
{\displaystyle \xi \geqslant 0}
μ
⩽
x
⩽
μ
−
σ
/
ξ
{\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }
ξ
<
0
{\displaystyle \xi <0}
Функція щільності є розв'язком диференційного рівняння :
{
f
′
(
x
)
(
−
μ
ξ
+
σ
+
ξ
x
)
+
(
ξ
+
1
)
f
(
x
)
=
0
,
f
(
0
)
=
(
1
−
μ
ξ
σ
)
−
1
ξ
−
1
σ
}
{\displaystyle \left\{{\begin{array}{l}f'(x)(-\mu \xi +\sigma +\xi x)+(\xi +1)f(x)=0,\\f(0)={\frac {\left(1-{\frac {\mu \xi }{\sigma }}\right)^{-{\frac {1}{\xi }}-1}}{\sigma }}\end{array}}\right\}}
Якщо параметри форми
ξ
{\displaystyle \xi }
μ
{\displaystyle \mu }
експоненційним розподілом .
Якщо параметр форми
ξ
>
0
{\displaystyle \xi >0}
μ
=
σ
/
ξ
{\displaystyle \mu =\sigma /\xi }
розподілу Парето з параметрами масштабу
x
m
=
σ
/
ξ
{\displaystyle x_{m}=\sigma /\xi }
α
=
1
/
ξ
{\displaystyle \alpha =1/\xi }
Якщо
X
{\displaystyle X}
∼
{\displaystyle \sim }
G
P
D
{\displaystyle GPD}
(
{\displaystyle (}
μ
=
0
{\displaystyle \mu =0}
σ
{\displaystyle \sigma }
ξ
{\displaystyle \xi }
)
{\displaystyle )}
Y
=
log
(
X
)
{\displaystyle Y=\log(X)}
∼
{\displaystyle \sim }
e
x
G
P
D
{\displaystyle exGPD}
(
{\displaystyle (}
μ
=
0
{\displaystyle \mu =0}
σ
{\displaystyle \sigma }
ξ
{\displaystyle \xi }
)
{\displaystyle )}
експоненційний узагальнений розподіл Парето . На відміну від УРП, exGPD має моменти всіх порядків, незалежно від його параметрів та інтерпретацій параметрів масштабу і форми, що робить оцінки параметрів більш ефективними.
УРП дуже схожий на Картавий розподілу. [ ред. | ред. код ] Якщо U є рівномірно розподіленою на
(0, 1], тоді
X
=
μ
+
σ
(
U
−
ξ
−
1
)
ξ
∼
GPD
(
μ
,
σ
,
ξ
≠
0
)
{\displaystyle X=\mu +{\frac {\sigma (U^{-\xi }-1)}{\xi }}\sim {\mbox{GPD}}(\mu ,\sigma ,\xi \neq 0)}
і
X
=
μ
−
σ
ln
(
U
)
∼
GPD
(
μ
,
σ
,
ξ
=
0
)
.
{\displaystyle X=\mu -\sigma \ln(U)\sim {\mbox{GPD}}(\mu ,\sigma ,\xi =0).}
Обидві формули отримані шляхом інверсії СГО.
У статистичних пакеті MATLAB, легко можна згенерувати вибірку узагальнено Парето розподілених випадкових чисел використовуючи команду "gprnd".
[ ред. | ред. код ] В УРП випадкова величина може бути виражена у вигляді експоненційної випадкової величини з гамма-розподіленим параметром інтенсивности.
X
|
Λ
∼
E
x
p
(
Λ
)
{\displaystyle X|\Lambda \sim Exp(\Lambda )}
і
Λ
∼
G
a
m
m
a
(
α
,
β
)
{\displaystyle \Lambda \sim Gamma(\alpha ,\beta )}
тоді
X
∼
G
P
D
(
ξ
=
1
/
α
,
σ
=
β
/
α
)
{\displaystyle X\sim GPD(\xi =1/\alpha ,\ \sigma =\beta /\alpha )}
Однак зауважимо, що оскільки параметри гамма розподілу має бути більшим нуля, ми отримаємо додаткові обмеження:
ξ
{\displaystyle \xi }
Розподіл задирок
Розподіл Парето GAV розподіл
Пикандса–Балкемы–теорема де Хаан
↑ Coles, Stuart (12 грудня 2001). An Introduction to Statistical Modeling of Extreme Values ISBN 9781852334598 (англ.) ↑ Dargahi-Noubary, G. R. (1989). On tail estimation: An improved method. Mathematical Geology . 21 (8): 829—842. doi :10.1007/BF00894450 . (англ.) ↑ Hosking, J. R. M.; Wallis, J. R. (1987). Parameter and Quantile Estimation for the Generalized Pareto Distribution . Technometrics . 29 (3): 339—349. doi :10.2307/1269343 . (англ.) ↑ Davison, A. C. (30 вересня 1984). Modelling Excesses over High Thresholds, with an Application. У de Oliveira, J. Tiago (ред.). Statistical Extremes and Applications ISBN 9789027718044 ↑ Embrechts, Paul; Klüppelberg, Claudia; Mikosch, Thomas (1 січня 1997). Modelling extremal events for insurance and finance ISBN 9783540609315
Pickands, James (1975). Statistical inference using extreme order statistics . Annals of Statistics . 3 : 119—131. doi :10.1214/aos/1176343003 . (англ.) Balkema, A.; De Haan, Laurens (1974). Residual life time at great age . Annals of Probability . 2 (5): 792—804. doi :10.1214/aop/1176996548 . (англ.) Lee, Se Yoon; Kim, J.H.K. (2018). Exponentiated generalized Pareto distribution:Properties and applications towards extreme value theory . Communications in Statistics - Theory and Methods . 0 : 1—25. doi :10.1080/03610926.2018.1441418 . (англ.) N. L. Johnson; S. Kotz; N. Balakrishnan (1994). Continuous Univariate Distributions Volume 1, second edition . New York: Wiley. ISBN 0-471-58495-9 Chapter 20, Section 12: Generalized Pareto Distributions. (англ.) Barry C. Arnold (2011). Chapter 7: Pareto and Generalized Pareto Distributions. У Duangkamon Chotikapanich (ред.). Modeling Distributions and Lorenz Curves ISBN 9780387727967 (англ.) Arnold, B. C.; Laguna, L. (1977). On generalized Pareto distributions with applications to income data . Ames, Iowa: Iowa State University, Department of Economics. (англ.)
Дискретні одновимірні Дискретні одновимірні Неперервні одновимірні Неперервні одновимірні Неперервні одновимірні Неперервні одновимірні Змішані Багатовимірні (спільні) Напрямкові Вироджені та сингулярні [en] Сімейства



















![{\displaystyle e^{\theta \mu }\,\sum _{j=0}^{\infty }\left[{\frac {(\theta \sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cf9f358ac58dcba4130cba492879256576e783)



































