Куб
| Куб | |
|---|---|

Натисніть тут, щоб подивитися обертання моделі | |
| Тип | Правильний багатогранник |
| Властивості | Опуклий, рівносторонній,однорідний, вершинно-транзитивний, гране-транзитивний, зоноедр, багатогранник Ганнера |
| Комбінаторика | |
| Елементи | 6 граней {4}; 12 ребер; 8 вершин (3-го степеня). |
| Грані | 6 квадратів
|
| Характеристика Ейлера | |
| Конфігурація вершини | 4.4.4 = 43 В кожній вершині сходяться 3 квадрати. |
| Конфігурація грані | V 3.3.3.3 = V (3)4 |
| Вершинна фігура |  Правильний трикутник з довжиною сторони |
| Класифікація | |
| Позначення | • C (в нотації Конвея[en] ) • P4 (в нотації Стюарта) • U06 (як однорідний багатогранник) • C18 (в нотації Г. Коксетера) • W3 (в нотації М. Веннінґера) |
| Символ Шлефлі | |
| Як квадратна призма: або Як прямокутний паралелепіпед: або [1] | |
| Символ Витгоффа[en] | 3 | 2 4 |
| Діаграма Коксетера-Динкіна | |
| Діаграма Шлегеля | 
|
| Група симетрії | Oh[en], B3, [4,3], (*432), порядок 48 (Повна симетрія правильного октаедра) |
| Група обертань | O, [4,3]+, (432), порядок 24 |
| Двоїстий багатогранник | Правильний октаедр 
|
| Розгортка | 
|
Куб (від лат. cubus і далі від дав.-гр. κύβος, первісно — «кубічна кістка для гри»)[2] або правильний гекса́едр (від дав.-гр. ἑξα- — «шість» + ἕδρα — «грань, поверхня») — правильний шестигранник, поверхня якого складена з шести квадратів, є одним з п’яти опуклих правильних багатогранників (тіл Платона).

Куб складений з 6 квадратних граней.
Має 12 ребер однакової довжини та 8 вершин (у кожній сходяться 3 ребра). Кожна вершина куба є вершиною трьох квадратів.
Куб також є квадратним паралелепіпедом, рівностороннім кубоїдом, прямим (правильногранним) ромбоедром, правильною квадратною призмою, прямокутним трикутним трапецоедром[en]. Куб є зоноедром та параллелоедром[en].
Куб є мірним багатогранником тривимірного простору. Тобто куб з довжиною ребра є одиницею виміру об'єму простору (так само як квадрат є одиницею вимірювання площі).
Куб має повну октаедричну симетрію[en] Oh, групу Коксетера [4,3], порядку 48, з абстактною структурою групи S4 × Z2.
Підгрупа із 24 симетрій обертання (тих, що зберігають орієнтацію простору) ізоморфна групі S4 перестановок з 4 елементів.

Куб має 13 осей обертової симетрії:
‒ 3 осі 4-го порядку — проходять через центри протилежних граней; (поворот на 90°, 180° і 270°);
‒ 4 осі 3-го порядку — проходять через протилежні вершини; (поворот на 120° і 240°);
‒ 6 осей 2-го порядку — проходять через середини протилежних паралельних ребер (поворот на 180°).
Має 9 площин дзеркальної симетрії: 3 з них проходять через середини паралельних реберта перпеддикулярні до них, а 6 — через діагоналі протилежних граней (через протилежні паралельні ребра куба).
Має центр симетрії (в ньому перетинаються всі осі та площини симетрії).
Сума плоских кутів при кожній з 8 вершин дорівнює 270°.
У різних дисциплінах використовуються значення терміна, що мають відношення до тих або інших властивостей геометричного прототипу. Зокрема, в алгебрі кубом числа називають значення цього числа, піднесене до 3-го степеня. В аналітиці (OLAP-аналіз) застосовуються так звані аналітичні багатовимірні куби, що дозволяють в наочному вигляді зіставити дані з різних таблиць.
- Куб має найбільший об'єм серед прямокутних паралелепіпедів із такою ж площею поверхні. А також куб, має найбільший об'єм серед прямокутних паралелепіпедів із такими ж загальними лінійними розмірами (довжина+висота+ширина).
- Площини, що проходять перпендикулярно до осей симетрії куба, утворюють перерізи у вигляді правильних багатокутників. [3]
Зокрема, переріз куба площиною, перпендикулярною до осей симетрії 4-го порядку, є квадратом. Перерізом куба площиною, перпендикулярною до осей симетрії 3-го порядку (діагоналей куба), може бути:
- правильний трикутник ; Найбільший за площею переріз у вигляді правильного трикутника (проходить через три вершини куба) ділить діагональ куба у співвідношенні 2:1;
- правильний шестикутник (якщо площина проходить також через центр куба; таких перерізів у куба є 4);
- напівправильний рівнокутний шестикутник (має два типи ребер, що чергуються між собою).
Також 12 перерізів куба площинами, перпендикулярними до осей симетрії 2-го порядку, є квадратами. Ці перерізи знаходяться на відстані від діагональних площин симетрії.
-
Переріз куба у вигляді правильного трикутника
-
Переріз куба у вигляді квадрата
-
Переріз куба у вигляді правильного шестикутника
-
Переріз куба у вигляді квадрата
- Куб утворює стільник, тобто кубами можна замостити тривимірний простір без проміжків та накладень. Куб є єдиним правильним багатогранником, що має таку властивість.
Тобто, існує одинадцять способів зробити із куба пласку розгортку, розрізаючи його по семи ребрах.
- Для того, щоб зафарбувати куб так, що сусідні грані не матимуть однакового кольору, необхідно принаймні три кольори.

Куб та правильний октаедр є взаємно двоїстими багатогранниками. Тобто центри граней куба відповідають вершинам правильного октаедра, і навпаки, центри граней правильного октаедра відповідають вершинам куба.
Якщо куб має ребро довжиною 1, то його топологічно двоїстий октаедр (вершини знаходяться в центрах граней початкового куба) має ребро довжиною , а канонічно двоїстий октаедр (напіввписані сфери канонічно-двоїстої пари багатогранників збігаються) має ребро довжиною [5]
- У куб можна вписати правильний октаедр таким чином, що всі шість вершин октаедра будуть суміщені з центрами шести граней куба.
- Куб можна вписати в правильний октаедр таким чином, що всі вісім вершин куба будуть розташовані в центрах восьми граней октаедра.
- У куб можна вписати правильний тетраедр двома способами таким чином, що чотири вершини тетраедра будуть суміщені з чотирма вершинами куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і збігатимуться з його граневими діагоналями.
- Куб можна вписати в вершини правильного додекаедра. При цьому ребра куба будуть збігатися з граневими діагоналями додекаедра.
В вершини додекаедра можливо вписати п'ять різних кубів. При цьому буде утворено однорідне з'єднання багатогранників — з'єднання п'яти кубів[en].
- У куб можна вписати правильний ікосаедр, при цьому, шість взаємно паралельних ребер ікосаедра будуть розташовані відповідно на шести гранях куба, решта 24 ребра всередині куба, всі дванадцять вершин ікосаедра лежатимуть на шести гранях куба.

Для куба, довжина ребер якого дорівнює :
| Діагональ грані | Радіус вписаної сфери (дотична до всіх граней) |
||
| Просторова діагональ | Радіус напіввписаної сфери (дотична до всіх ребер) |
||
| Радіус описаної сфери (проходить через всі вершини) |
|||
| Площа поверхні | |||
| Об'єм | Двогранний кут між гранями | (радіан) | |
| Тілесний кут при вершині | (стерадіан) | ||
| Сферичність | Тілесний кут, під яким грань видно з центру куба |
(стерадіан) | |
Куб має найбільший об'єм серед прямокутних паралелепіпедів із такою ж площею поверхні. А також куб, має найбільший об'єм серед прямокутних паралелепіпедів, вписаних в задану сферу та серед прямокутних паралелепіпедів із такими ж загальними лінійними розмірами (довжина+висота+ширина).
Центр масс куба знаходиться в його геометричному центрі.
Момент інерції суцільного куба з масою m та довжиною ребра a (вісь обертання проходить через центри протилежних граней):[8]
Нехай описана сфера куба має радіус R. Нехай дано довільну точку в просторі і відстані від неї до вершин куба дорівнюють di . Тоді виконується рівність: [9] [10]
Якщо точка знаходиться на описаній сфері куба, то виконується рівність:[10]
Декартові координати восьми вершин куба з довжиною ребра , центр якого знаходиться в початку координат, мають значення:
Вісім вершин куба лежать по чотири у двох паралельних площинах (паралельних до площини Oxy), утворюючи в них два квадрати.
При цьому осі координат Ox, Oy та Oz збігаються з осями обертової симетрії 4-го порядку, а координатні площини Oxz, Oyz та Oxy є площинами дзеркальної симетрії куба. Центр багатогранника знаходиться в початку координат.
Для всіх внутрішніх точок (x0, x1, x2) цього куба виконується нерівність :
| Граф куба | |
|---|---|
 4-fold symmetry | |
| Вершин | 8 |
| Ребер | 12 |
| Радіус | 3 |
| Діаметр | 3 |
| Обхват | 4 |
| Автоморфізм | 48 |
| Хроматичне число | 2 |
| Властивості | Регулярний, планарний, багатогранний, простий, зв'язний, симетричний Гамільтонів, граф Келі, циклічний , кубічний, вершинно-транзитивний, реберно-транзитивний, дистанційно-транзитивний, двочастковий, дистанційно-регулярний, 3-вершинно-зв'язний граф |
В теорії графів граф куба — це граф з 8 вершинами та 12 ребрами, що має кістяк куба.[11]
Всі 8 вершин графа мають степінь 3, а отже, граф є кубічним.
Цей граф є окремим випадком графа гіперкуба.[12] Також він є одним з 5 платонових графів, кістяк якого є багатогранником Платона.
Узагальненням графа куба є тривимірний k-ARY граф Геммінга, який для k = 2 є кубічним графом. Графи такого типу зустрічаються в теорії паралельних обчислень в комп'ютерах.

Граф куба має 12 різних гамільтонових циклів. Гамільтонів цикл — замкнений шлях, що проходить через кожну вершину графа рівно один раз.
Граф куба не має ейлерових циклів.
Реберним графом для графа куба є граф кубооктаедра.
Куб має чотири спеціальні ортогональні проєкції, із центом, на одній з вершин, ребрі, грані і нормалі відносно її фігури вершин. Перша і друга відповідають A2 і B2 площинам Коксетера.
| Центровані по | Грані | Вершині |
|---|---|---|
| Площини Коксетера | B2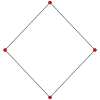
|
A2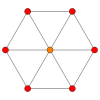
|
| Проєктивна симетрія |
[4] | [6] |
| Фронтальний вид та вид під нахилом |
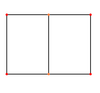
|

|
Куб може бути представлений як сферичний багатогранник і спроектований на площину за допомогою стереографічної проекції. Ця проекція є конформною, тобто зберігає кути, але не площі чи довжини. Прямі лінії на сфері проєктуються на площину як дуги кола.

|

|
| Ортографічна проєкція | Стереографічна проєкція |
|---|
Куб є єдиним правильним багатогранником, яким можна замостити тривимірний простір без проміжків та накладень.
Також тривимірний евклідів простір можна заповнити без проміжків за допомогою кубів в комбінації з багатогранниками Архімеда (і призмами) з однаковою довжиною ребра. Такі тривимірні паркети, що заповнюють простір, називаються стільниками. Наступні стільники містять куби:
-
Стільник з кубів
Куб в довільній розмірності простору n також називають n-вимірним кубом або гіперкубом, або просто n-кубом. Гіперкуби в кожній розмірності простору тако́ж є правильними політопами, а та́кож мірними політопами (по аналогії як у квадратах вимірюють площу, а в кубах — об'єм).
n-вимірний куб має гіперграней розмірності k , що його обмежують[15].
Наприклад:
- Нульвимірний куб (точка) має 1 вершину;
- Одновимірний куб (відрізок) має 2 вершини;
- Двовимірний куб (квадрат) має 4 вершини і 4 ребра;
- Чотиривимірний гіперкуб (тесеракт) має 16 вершин, 32 ребра, 24 грані (квадрати) і 8 комірок (куби);
- n-вимірний гіперкуб має:
Гіперплоща n-вимірного гіперкуба з довжиною ребра 2 дорівнює ;
Гіпероб'єм n-вимірного гіперкуба з довжиною ребра 2 дорівнює .[15]
Моделлю для n-вимірного куба є одиничний куб у векторному просторі . А саме, замкнений одиничний куб має вигляд
- , -кратний декартів добуток одиничного інтервалу
- Опукла оболонка вершин з координатами та
- Перетин множин півпросторів та
Одиничний куб — це паралельний координатним осям куб з довжиною ребра і вершиною у початку координат. Узагальненням цього поняття є кубоїди в , які відіграють важливу роль у багатовимірному аналізі. [15]
Куб можна розглядати як окремі випадки інших типів багатогранників. В цьому випадку куб буде мати не повну октаедричну симетрію[en] Oh , а симертії, які є підгрупами повної групи. Тобто куб, як частинний випадок призм, кубоїдів, трапецоедрів — є менш симетричним, ніж куб як правильний багатогранник. Це також можна побачити в розфарбовці його граней.
Куб має три однорідні розфарбування, названі за унікальними кольорами квадратних граней навколо кожної вершини: 111, 112, 123.
Куб має чотири класи симетрії, які можна представити за допомогою вершинно-транзитивного розфарбовування граней. Найвища октаедрична симетрія Oh має всі грані однакового кольору. Діедрична симетрія[en] D4h походить від куба,що є тілом,всі шість граней якого забарвлені в різні кольори. Призматична підмножина D2d має таке ж забарвлення, як і попередня, а D2h має почергове забарвлення граней — попарно протилежні грані забарвлені в три кольори. Кожна форма симетрії має свій символ Витгоффа[en].
| Назва | Правильний шестигранник | Квадратна призма | Прямокутна трапецієва призма | Прямокутний паралелепіпед | Прямокутна ромбічна призиа | Трикутний трапецоедр |
|---|---|---|---|---|---|---|
| Діаграми Коксетера — Динкіна | ||||||
| Символ Шлефлі | {4,3} | {4}×{ } rr{4,2} |
s2{2,4} | { }3 tr{2,2} |
{ }×2{ } | |
| символ Витгоффа[en] | 3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
| Симетрія | Oh [4,3] (*432) |
D4h [4,2] (*422) |
D2d [4,2+] (2*2) |
D2h [2,2] (*222) |
D3d [6,2+] (2*3) | |
| Порядок симетрії | 24 | 16 | 8 | 8 | 12 | |
| Зображення (з однорідним розфарбуванням) |
 (111) |
 (112) |
 (112) |
 (123) |
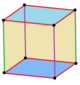 (112) |
 (111), (112) |
Куб можна розрізати на шість однакових квадратних пірамід. Якщо ці квадратні піраміди приєднати до граней іншого куба, то отримаємо багатогранник, візуально схожий на
ромбододекаедр (з парами компланарних трикутників, об'єднаних у ромбічні грані).
Однак багатогранник з таким способом побудови схожий лише візуально на ромбододекаедр, але топологічно він еквівалентний до тетракіс куба[en] (одного з напівправильних багатогранників Каталана), оскільки має додаткові вершини і ребра, що належать цим пірамідам (дві бічні грані пірамід знаходяться в одній площині і візуально створюють враження однієї ромбічної грані).
Геометрична операція зрізання, застосована до куба, утворює чотири однорідних багатогранники на певних стадіях процесу зрізання.
Зрізаний куб є опуклим однорідним багатогранником U09, одним з напівправильних багатогранників Архімеда що має діаграму Коксетера — Динкіна ![]()
![]()
![]()
![]()
![]() та символ Шлефлі t{4,3}. Утворюється при зрізанні вершин куба до моменту, коли всі грані стають правильними багатокутниками. Має 14 граней (8 правильних трикутників та 6 правильних восьмикутників), 36 ребер та 24 вершини.
та символ Шлефлі t{4,3}. Утворюється при зрізанні вершин куба до моменту, коли всі грані стають правильними багатокутниками. Має 14 граней (8 правильних трикутників та 6 правильних восьмикутників), 36 ребер та 24 вершини.
Кубооктаедр утворюється при повному зрізанні[en] (ректифікації) куба, коли зрізання вершин проводиться до точок, що лежать на серединах ребер багатогранника, тобто ребра початкового багатогранника фактично зникають.Він є опуклим однорідним багатогранником U07, одним з напівправильних багатогранників Архімеда. Має 14 граней (8 правильних трикутників та 6 квадратів), 24 ребер та 12 вершин.
Подальше зрізання (глибоке зрізання[en] або бітрункація) призводить до появи зрізаного октаедра, Процес зрізання проводиться до моменту, коли грані від зрізаних вершин початкового куба (трикутні грані) стануть правильними шестикутниками. Зрізаний октаедр є опуклим однорідним багатогранником U08, одним з напівправильних багатогранників Архімеда. Має 14 граней (8 правильних шестикутників та 6 квадратів), 36 ребер та 24 вершини.
Процес зрізання куба завершується (при повному глибокому зрізанні або біректифікації) утворенням двоїстого до нього багатогранника — правильного октаедра, коли грані початкового багатогранника зменшуються до точок, тобто фактично зникають.
| Назва | Куб | Зрізаний куб | Кубооктаедр | Зрізаний октаедр | Правильний октаедр |
|---|---|---|---|---|---|
| Діаграма Коксетера — Динкіна | x4o3o |
x4x3o |
o4x3o |
o4x3x |
x4x3o |
| Символ Шлефлі | {4,3} | t{4,3} | r{4,3} | t{3,4} | {3,4} |
| Зображення | 
|

|

|

|

|
| Однорідні октаедричні многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симетрія: [4,3], (*432)[en] | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Двоїсті многогранники | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
| Файл:RhombicDodecahedron.svg | Файл:DisdyakisDodecahedron.svg | |||||||||
Деякі багатогранники Джонсона можна утворити шляхом нарощення граней куба квадратними пірамідами (J1):
- Подовжена чотирикутна піраміда (J8 ) — нарощено одну грань;
- Подовжена чотирикутна біпіраміда (J15) — нарощено дві протилежні грані.
При застосуванні щодо куба геометричної операції Зрізання носів[en] (снубифікація), отримаємо напівправильний багатогранник Архімеда — кирпатий куб.
При застосуванні щодо куба геометричної операції Фаска[en] (зрізання ребер), отримаємо багатогранник Ґолдберга[en] — куб з фаскою[en].

|

|

|
| Кирпатий куб | Куб з малою фаскою | Куб з фаскою[en] |
|---|
Два однорідних з'єднання багатогранників складаються з кубів:
| З'єднання трьох кубів[en] | З'єднання п'яти кубів[en] |
|---|---|

|

|
| Симетрія n32 |
Сферична | Евклідова | Компактна гіперболічна |
Паракомп. | ||||
|---|---|---|---|---|---|---|---|---|
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Кирпаті фігури |

|

|

|

|

|

|

|

|
| Конфігурація | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Фігури | 
|

|

|

|

|

|

| |
| Конфігурація | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |

| Багатокутник Петрі[en] куба | ||||
|---|---|---|---|---|

|

|

|

|

|
| Просторовими багатокутниками Петрі[en] куба є 4 просторових шестикутників. | ||||
- Шестигранники
- Блазенський ковпак
- Кубічне число — вид фігурних чисел.
- Подвоєння куба — одна з класичних задач давнини.
- Кубик Рубика — головоломка у вигляді куба.
- Кубічна піраміда
- ↑ N. W. Johnson, 2018.
- ↑ Етимологічний словник української мови : в 7 т. / редкол.: О. С. Мельничук (гол. ред.) та ін. — К. : Наукова думка, 1989. — Т. 3 : Кора — М / Ін-т мовознавства ім. О. О. Потебні АН УРСР ; укл.: Р. В. Болдирєв та ін. — 552 с. — ISBN 5-12-001263-9.
- ↑ Gérard Villemin. Section du cube. Процитовано 3 octobre 2019..
- ↑ Edkins, Jo (2007). Cube. Solid shapes and their nets (англ.) . Архів оригіналу за 26 грудня 2019.
- ↑ а б Weisstein, Eric W. Cube(англ.) на сайті Wolfram MathWorld.
- ↑ Richard Goldstone, Robert Suzzi Valli, 2016.
- ↑ All 11 Folding Nets of the Cube - Wolfram Demonstrations Project. demonstrations.wolfram.com. Процитовано 30 травня 2024.
- ↑ Cube inertia tensor - Wolfram Alpha. www.wolframalpha.com (англ.) .
- ↑ Poo-Sung Park. Regular polytope distances. — Forum Geometricorum, 2016. — Т. 16. — С. 227-232. — ISSN 1534-1178. Архівовано з джерела 10 жовтня 2016.
- ↑ а б Meskhishvili, Mamuka (2020). Cyclic Averages of Regular Polygons and Platonic Solids. Communications in Mathematics and Applications. 11: 335—355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420.
- ↑ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs (англ.) . Oxford University Press.
- ↑ Harary, Frank; Hayes, John P.; Wu, Horng-Jyh (1988). A survey of the theory of hypercube graphs (PDF). Computers & Mathematics with Applications. 15 (4): 277—289. doi:10.1016/0898-1221(88)90213-1. MR 0949280.
- ↑ Eric Weisstein. Cubical Graph. mathworld.wolfram.com (англ.) .
- ↑ Cubical Graph. wolframalpha.com (англ.) .
- ↑ а б в Martin Henk, Jürgen Richter-Gebert, 1999.
- N. W. Johnson. Розділ 11: Finite symmetry groups — Дивись 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c. // Geometries and Transformations. — Cambridge University Press / United Kingdom, 2018. — P. 234. — ISBN 978-1-107-10340-5.
- Richard Goldstone, Robert Suzzi Valli. Unfoldings of the Cube. — 2016. — С. 17. — DOI:.
- Martin Henk, Jürgen Richter-Gebert, Günter M. Ziegler. Basic properties of convex polytopes. — Technische Universität Berlin, 1999. — С. 243-270. — DOI:.
- Куб // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 114. — ISBN 978-966-7407-83-4.
- Weisstein, Eric W. Cube(англ.) на сайті Wolfram MathWorld.
- Cube(англ.) на сайті Polytope Wiki.
- Cube (англ.) на сайті dmccooey.com.
- Klitzing, Richard. "cube".
- Quickfur. "The Cube"
- Wedd, N. "The Cube"
- Hi.gher.Space Wiki Contributors. "Cube"
- Paper Models of Polyhedra [Архівовано 26 лютого 2013 у Wayback Machine.]
- The Uniform Polyhedra [Архівовано 11 лютого 2008 у Wayback Machine.]
- Virtual Reality Polyhedra [Архівовано 23 лютого 2008 у Wayback Machine.]



































![{\displaystyle \Psi ={\sqrt[{3}]{\frac {\pi }{6}}}\approx 0.805995}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f301a2db3019fad8f5dd978b56b5ff814372e05e)





























![{\displaystyle I^{n}=[0,1]\times \cdots \times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fa17f870540204d44b501791c78c5cadd0f77f)






