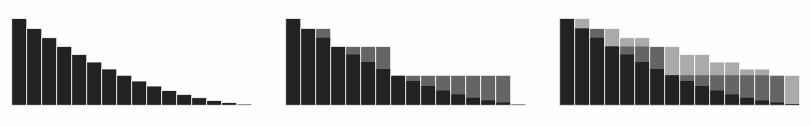Ознака стиснення Коші — названа на честь Огюстена-Луї Коші , є однією з ознак збіжності для нескінченних рядів .
Для незростаючої послідовності
f
(
n
)
{\displaystyle f(n)}
дійсних чисел , ряд
∑
n
=
1
∞
f
(
n
)
{\textstyle \sum \limits _{n=1}^{\infty }f(n)}
збігається тоді й лише тоді , коли «ущільнений» ряд
∑
n
=
0
∞
2
n
f
(
2
n
)
{\textstyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})}
∑
n
=
1
∞
f
(
n
)
≤
∑
n
=
0
∞
2
n
f
(
2
n
)
≤
2
∑
n
=
1
∞
f
(
n
)
,
{\displaystyle \sum _{n=1}^{\infty }f(n)\leq \sum _{n=0}^{\infty }2^{n}f(2^{n})\leq \ 2\sum _{n=1}^{\infty }f(n),}
Погрупуємо доданки в групи з довжиною рівною степеню двійки (1, 2, 4, …):
∑
n
=
1
∞
f
(
n
)
=
f
(
1
)
+
(
f
(
2
)
+
f
(
3
)
)
+
(
f
(
4
)
+
f
(
5
)
+
f
(
6
)
+
f
(
7
)
)
+
⋯
≤
f
(
1
)
+
(
f
(
2
)
+
f
(
2
)
)
+
(
f
(
4
)
+
f
(
4
)
+
f
(
4
)
+
f
(
4
)
)
+
⋯
=
f
(
1
)
+
2
f
(
2
)
+
4
f
(
4
)
+
⋯
=
∑
n
=
0
∞
2
n
f
(
2
n
)
{\displaystyle {\begin{array}{rcccccccl}\displaystyle \sum \limits _{n=1}^{\infty }f(n)&=&f(1)&+&{\Big (}f(2)+f(3){\Big )}&+&{\Big (}f(4)+f(5)+f(6)+f(7){\Big )}&+&\cdots \\&\leq &f(1)&+&{\Big (}f(2)+f(2){\Big )}&+&{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}&+&\cdots \\&=&f(1)&+&2f(2)&+&4f(4)&+&\cdots =\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})\end{array}}}
Погрупуємо доданки результату в групи з довжиною рівною степеню двійки по іншому (2, 4, 8, …):
∑
n
=
0
∞
2
n
f
(
2
n
)
=
f
(
1
)
+
(
f
(
2
)
+
f
(
2
)
)
+
(
f
(
4
)
+
f
(
4
)
+
f
(
4
)
+
f
(
4
)
)
+
⋯
=
(
f
(
1
)
+
f
(
2
)
)
+
(
f
(
2
)
+
f
(
4
)
+
f
(
4
)
+
f
(
4
)
)
+
⋯
≤
(
f
(
1
)
+
f
(
1
)
)
+
(
f
(
2
)
+
f
(
2
)
)
+
(
f
(
3
)
+
f
(
3
)
)
+
⋯
=
2
∑
n
=
1
∞
f
(
n
)
{\displaystyle {\begin{aligned}\sum _{n=0}^{\infty }2^{n}f(2^{n})&=f(1)+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}+\cdots \\&={\Big (}f(1)+f(2){\Big )}+{\Big (}f(2)+f(4)+f(4)+f(4){\Big )}+\cdots \\&\leq {\Big (}f(1)+f(1){\Big )}+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(3)+f(3){\Big )}+\cdots =2\sum _{n=1}^{\infty }f(n)\end{aligned}}}
Візуалізація подвійної нерівності. Часткові суми (інші мови) рядів
∑
f
(
n
)
,
∑
2
n
f
(
2
n
)
,
2
∑
f
(
n
)
{\textstyle \sum f(n),\;\sum 2^{n}f(2^{n}),\;2\sum f(n)}
Заміна
f
(
n
)
→
2
n
f
(
2
n
)
{\textstyle f(n)\rightarrow 2^{n}f(2^{n})}
x
→
e
x
{\textstyle x\rightarrow e^{x}}
f
(
x
)
d
x
→
e
x
f
(
e
x
)
d
x
{\textstyle f(x)\,\mathrm {d} x\rightarrow e^{x}f(e^{x})\,\mathrm {d} x}
По аналогії з інтегральною ознакою Маклорена — Коші , для монотонної функції
f
{\displaystyle f}
∑
n
=
1
∞
f
(
n
)
{\textstyle \sum \limits _{n=1}^{\infty }f(n)}
∫
1
∞
f
(
x
)
d
x
{\displaystyle \displaystyle \int _{1}^{\infty }f(x)\,\mathrm {d} x}
Підстановка
x
→
2
x
{\textstyle x\rightarrow 2^{x}}
log
2
∫
2
∞
2
x
f
(
2
x
)
d
x
{\displaystyle \displaystyle \log 2\ \int _{2}^{\infty }\!2^{x}f(2^{x})\,\mathrm {d} x}
log
2
∫
2
∞
2
x
f
(
2
x
)
d
x
<
log
2
∫
0
∞
2
x
f
(
2
x
)
d
x
{\displaystyle \displaystyle \log 2\ \int _{2}^{\infty }\!2^{x}f(2^{x})\,\mathrm {d} x<\log 2\ \int _{0}^{\infty }\!2^{x}f(2^{x})\,\mathrm {d} x}
∑
n
=
0
∞
2
n
f
(
2
n
)
{\textstyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})}
∑
n
=
1
∞
f
(
n
)
{\textstyle \sum \limits _{n=1}^{\infty }f(n)}
∑
n
=
0
∞
2
n
f
(
2
n
)
{\textstyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})}
Тест може бути корисним при наявності n у знаменнику f
Найпростіший приклад: гармонійний ряд
∑
n
=
1
∞
1
/
n
{\textstyle \sum _{n=1}^{\infty }1/n}
∑
1
{\textstyle \sum 1}
f
(
n
)
:=
n
−
a
(
log
n
)
−
b
(
log
log
n
)
−
c
.
{\displaystyle f(n):=n^{-a}(\log n)^{-b}(\log \log n)^{-c}.}
Ряд є розбіжним для a > 1a < 1a = 1
∑
n
−
b
(
log
n
)
−
c
.
{\displaystyle \sum n^{-b}(\log n)^{-c}.}
Тому за аналогією: ряд є розбіжним для b > 1b < 1b = 1c .
Аналогічним є алгоритм визначення збіжності для узагальненого ряду Бертрана
∑
n
≥
N
1
n
⋅
log
n
⋅
log
log
n
⋯
log
∘
(
k
−
1
)
n
⋅
(
log
∘
k
n
)
α
(
N
=
⌊
exp
∘
k
(
0
)
⌋
+
1
)
{\displaystyle \sum _{n\geq N}{\frac {1}{n\cdot \log n\cdot \log \log n\cdots \log ^{\circ (k-1)}n\cdot (\log ^{\circ k}n)^{\alpha }}}\quad \quad (N=\lfloor \exp ^{\circ k}(0)\rfloor +1)}
Де
f
∘
m
{\displaystyle f^{\circ m}}
m ітерація функції
f
{\displaystyle f}
f
∘
m
(
x
)
:=
{
f
(
f
∘
(
m
−
1
)
(
x
)
)
,
m
=
1
,
2
,
3
,
…
;
x
,
m
=
0.
{\displaystyle f^{\circ m}(x):={\begin{cases}f(f^{\circ (m-1)}(x)),&m=1,2,3,\ldots ;\\x,&m=0.\end{cases}}}
...