t-розподіл Стьюдента

t-Стьюдента
Щільність розподілу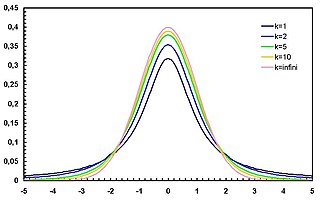
Функція розподілу ймовірностей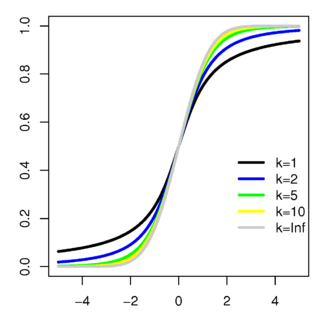
Параметри	$\nu >0$ ступені свободи (дійсне)
Носій функції	$x\in (-\infty ;+\infty )\!$
Розподіл імовірностей	${\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}\!$
Функція розподілу ймовірностей (cdf)	${\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma ({\frac {\nu }{2}})}}\end{matrix}}$ де 2F1 це гіпергеометрична функція
Середнє	$0$ для $\nu >1$, інакше невизначено
Медіана	$0$
Мода	$0$
Дисперсія	${\frac {\nu }{\nu -2}}$ для $\nu >2\!$, інакше невизначена
Коефіцієнт асиметрії	$0$ для $\nu >3$
Коефіцієнт ексцесу	${\frac {6}{\nu -4}}$ для $\nu >4\!$
Ентропія	${\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}$ $\psi$: дигамма-функція, $B$: Бета-функція
Твірна функція моментів (mgf)	(не визначена)
Характеристична функція	${\frac {K_{\nu /2}({\sqrt {\nu }}|t|)({\sqrt {\nu }}|t|)^{\nu /2}}{\Gamma (\nu /2)2^{\nu /2-1}}},\;\nu >0$ $K_{\nu }(x)$: бесселівська функція, див.

У теорії ймовірностей та статистиці t-розподіл чи t-розподіл Стьюдента — різновид розподілу ймовірностей, який виникає в задачі оцінення сподіваного значення нормально розподіленої популяції, коли розмір вибірки малий. Цей розподіл є основою популярного t-тесту Стьюдента статистичної значущості різниці математичних сподівань двох вибірок, та довірчого інтервалу різниці очікуваних значень двох вибірок. t-розподіл Стьюдента є також частковим випадком узагальненого гіперболічного розподілу. Розроблений В. С. Госсетом (псевдонім «Стьюдент»).

Як розподіл Стьюдента виникає з вибірки

Нехай X₁, …, X_n — це незалежні випадкові величини з розподілу N(μ, σ²), тобто це вибірка розміру n з популяції з нормальним розподілом з середнім значенням μ і дисперсією σ².

Нехай

${\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$

буде середнім вибірки і нехай

$S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}$

буде (виправлена згідно з Бесселем) дисперсія вибірки. Тоді випадкова величина

${\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}$

має стандартний нормальний розподіл (тобто, з середнім 0 і дисперсією 1), а випадкова величина

${\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}$

(де ми підставили S замість σ) має t-розподіл Стьюдента з n − 1 ступенями вільності. Через те що ми замінили $S$ на $\sigma ,$ єдина неспостережувана величина тут це $\mu ,$ отже ми можемо використати це, щоб знайти довірчі інтервали для $\mu .$ Зауважте, що незважаючи на те, що вони базуються на тій самій вибірці ${\textstyle X_{1},\ldots ,X_{n},}$ чисельник і знаменник у попередньому виразі — незалежні випадкові величини. Це можна побачити спостерігши, що ${\textstyle \operatorname {cov} ({\overline {X}},\,X_{i}-{\overline {X}})=0,}$ і згадавши, що ${\textstyle {\overline {X}}}$ і ${\textstyle X_{i}-{\overline {X}}}$ це дві лінійні комбінації тої самої множини н.о.р. нормально розподілених випадкових величин.

Означення

Щільність розподілу

Т-розподіл Стьюдента має функцію щільності розподілу, що задається формулою

$f(t)={\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {t^{2}}{\nu }}\right)^{-{\frac {\nu +1}{2}}},\!$

де $\nu$ — кількість ступенів вільності, $\Gamma$ — гамма-функція. Формула також може бути записана у вигляді

$f(t)={\frac {1}{{\sqrt {\nu }}\,B\left({\frac {1}{2}},{\frac {\nu }{2}}\right)}}\left(1+{\frac {t^{2}}{\nu }}\right)^{-{\frac {\nu +1}{2}}}\!,$

де B — бета-функція.

Для парних значень $\nu$

${\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}={\frac {(\nu -1)(\nu -3)\cdots 5\cdot 3}{2{\sqrt {\nu }}(\nu -2)(\nu -4)\cdots 4\cdot 2\,}}.$

Для непарних значень $\nu$

${\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}={\frac {(\nu -1)(\nu -3)\cdots 4\cdot 2}{\pi {\sqrt {\nu }}(\nu -2)(\nu -4)\cdots 5\cdot 3\,}}.\!$

Функція розподілу ймовірності

Функція розподілу може бути записана в термінах I, регуляризованої неповна бета-функція. Для t > 0

$\int _{-\infty }^{t}f(u)\,du=1-{\frac {1}{2}}I_{x(t)}\left({\frac {\nu }{2}},{\frac {1}{2}}\right),$

з

$x(t)={\frac {\nu }{t^{2}+\nu }}.$

Інші значення отримуються симетрично. Альтернативна формула дійсна для t² < ν, така

$\int _{-\infty }^{t}f(u)\,du={\frac {1}{2}}+t{\frac {\Gamma \left({\frac {\nu +1}{2}}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {t^{2}}{\nu }}\right)$

де ₂F₁ — певний випадок гіпергеометричної функції.

Особливі випадки

Для певних значень параметра $\nu$ розподіл Стьюдента має просту форму.

• $\nu =1$

Функція розподілу:

$F(x)={\tfrac {1}{2}}+{\tfrac {1}{\pi }}\arctan(x).$

Функція щільності:

$f(x)={\frac {1}{\pi (1+x^{2})}}.$

Див. Розподіл Коші

• $\nu =2$

Функція розподілу:

$F(x)={\tfrac {1}{2}}+{\frac {x}{2{\sqrt {2+x^{2}}}}}.$

Функція щільності:

$f(x)={\frac {1}{\left(2+x^{2}\right)^{\frac {3}{2}}}}.$

• $\nu =3$

Функція щільності:

$f(x)={\frac {6{\sqrt {3}}}{\pi \left(3+x^{2}\right)^{2}}}.$

• $\nu =\infty$

Функція щільності:

$f(x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}.$

Див. нормальний розподіл

Порівняння з нормальним розподілом

Загалом щільність t-розподілу схожа на дзвоноподібну функцію щільності нормального розподілу, з тією відмінністю, що у t-розподілу вона трохи нижча і ширша. За кількості ступенів свободи, що прямує до нескінченості, t-розподіл прямує до нормального розподілу з математичним сподіванням 0 і дисперсією 1.

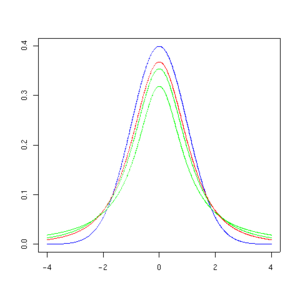
На графіках нижче показано щільності t-розподілу для зростаючих значень параметру $\nu$. Для порівняння, нормальний розподіл зображено синім. Можна помітити, що із збільшенням $\nu$ щільність t-розподілу наближається до нормального.

Щільність t-розподілу для 1, 3, 5, 30 ступенів вільності (зображено червоним) у порівнянні зі щільністю нормального розподілу (зображено синім). Зеленим показано щільності з меншою кількістю ступенів вільності."

• 
  1 ступінь вільності
• 
  3 ступені вільності
• 
  5 ступені вільності
• 
  30 ступенів вільності

Таблиця вибраних значень

Наступна таблиця містить кілька вибраних значень цього розподілу, з r ступенями свободи для інтервалів певності 90 %, 95 %, 97,5 % та 99,5 %. Ці числа «односторонні», тобто коли ми бачимо «90%», «4 ступенів свободи», та «1.533»,

це означає $\displaystyle Pr(T<1,533)=0,9;$

це не означає $\displaystyle Pr(-1,533<T<1,533)=0,9$

Тому, по симетрії розподілу, ми маємо

$\displaystyle Pr(T<-1,533)=Pr(T>1,533)=1-0,9=0,1$

та в результаті

$\displaystyle Pr(-1,533<T<1,533)=1-2\cdot 0,1=0,8.$

r	75 %	80 %	85 %	90 %	95 %	97.5 %	99 %	99.5 %	99.75 %	99.9 %	99.95 %
1	1.000	1.376	1.963	3.078	6.314	12.71	31.82	63.66	127.3	318.3	636.6
2	0.816	1.061	1.386	1.886	2.920	4.303	6.965	9.925	14.09	22.33	31.60
3	0.765	0.978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.21	12.92
4	0.741	0.941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0.727	0.920	1.156	1.476	2.015	2.571	3.365	4.032	4.773	5.893	6.869
6	0.718	0.906	1.134	1.440	1.943	2.447	3.143	3.707	4.317	5.208	5.959
7	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0.706	0.889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0.703	0.883	1.100	1.383	1.833	2.262	2.821	3.250	3.690	4.297	4.781
10	0.700	0.879	1.093	1.372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0.694	0.870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0.690	0.865	1.071	1.337	1.746	2.120	2.583	2.921	3.252	3.686	4.015
17	0.689	0.863	1.069	1.333	1.740	2.110	2.567	2.898	3.222	3.646	3.965
18	0.688	0.862	1.067	1.330	1.734	2.101	2.552	2.878	3.197	3.610	3.922
19	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861	3.174	3.579	3.883
20	0.687	0.860	1.064	1.325	1.725	2.086	2.528	2.845	3.153	3.552	3.850
21	0.686	0.859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0.685	0.858	1.060	1.319	1.714	2.069	2.500	2.807	3.104	3.485	3.767
24	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0.684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3.450	3.725
26	0.684	0.856	1.058	1.315	1.706	2.056	2.479	2.779	3.067	3.435	3.707
27	0.684	0.855	1.057	1.314	1.703	2.052	2.473	2.771	3.057	3.421	3.690
28	0.683	0.855	1.056	1.313	1.701	2.048	2.467	2.763	3.047	3.408	3.674
29	0.683	0.854	1.055	1.311	1.699	2.045	2.462	2.756	3.038	3.396	3.659
30	0.683	0.854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0.681	0.851	1.050	1.303	1.684	2.021	2.423	2.704	2.971	3.307	3.551
50	0.679	0.849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0.679	0.848	1.045	1.296	1.671	2.000	2.390	2.660	2.915	3.232	3.460
80	0.678	0.846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0.677	0.845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0.677	0.845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
$\infty$	0.674	0.842	1.036	1.282	1.645	1.960	2.326	2.576	2.807	3.090	3.291

Наприклад, якщо ми маємо вибірку з варіацією 2 та середнім значенням 10, вибраним з набору 11 елементів (10 ступенів свободи), використовуючи формулу:

${\overline {X}}_{n}\pm A{\frac {S_{n}}{\sqrt {n}}}$

Ми можемо визначити що з 90-відсотковою впевненістю ми маємо дійсне середнє значення, яке лежить в інтервалі:

$10+1.37218{\frac {\sqrt {2}}{\sqrt {11}}}=10.58510$

Та, знову з 90 % впевненістю, ми маємо дійсне середнє значення, яке лежить поза інтервалом:

$10-1.37218{\frac {\sqrt {2}}{\sqrt {11}}}=9.41490$

Так, з 80 % впевненістю, ми маємо дійсне середнє значення, яке лежить поміж:

$10\pm 1.37218{\frac {\sqrt {2}}{\sqrt {11}}}=[9.41490,10.58510]$

Література

• «Student» (W.S. Gosset) (1908) The probable error of a mean. Biometrika 6(1):1-25.
• M. Abramowitz and I. A. Stegun, eds. (1972) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. (See Section 26.7.)
• R.V. Hogg and A.T. Craig (1978) Introduction to Mathematical Statistics. New York: Macmillan.

Посилання

• VassarStats Density plot, critical values, etc., calculated for a user-specified number of d.f.
• Earliest Known Uses of Some of the Words of Mathematics (S) (Remarks on the history of the term «Student's distribution»)
• Distribution Calculator [Архівовано 29 січня 2007 у Wayback Machine.] Calculates probabilities and critical values for normal, t-, chi2- and F-distribution
• New Methods for Managing «Student's» T Distribution Surveys techniques for sampling with new techniques using the inverse CDF directly

Див. також

• Статистика
• Теорія ймовірностей