Фігури Ліссажу
| Фігури Ліссажу | |
 | |
| Названо на честь |
Жуль Антуан Ліссажу |
|---|---|
| Формула |
|
| Гештег |
LissajousCurve |
| Підтримується Вікіпроєктом |
Вікіпедія:Проєкт:Математика |
| | |
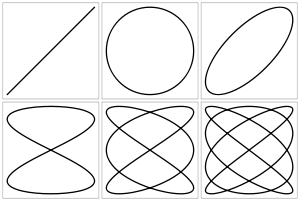
Фігури Ліссажу — замкнуті траєкторії, які прокреслюються точкою, що здійснює одночасно два гармонійних коливання у двох взаємно перпендикулярних напрямках. Вперше вивчені французьким науковцем Ж. Ліссажу (фр. J. Lissajous; 1822—1880). Вид фігур залежить від співвідношення між періодами (частотами), фазами і амплітудами обох коливань. У найпростішому випадку (за рівності обох періодів) фігури являють собою еліпси, які при різниці фаз 0 або π вироджуються у відрізки прямих, а при різниці фаз π/2 і рівності амплітуд перетворюються в коло. Якщо періоди обох коливань не точно збігаються, то різниця фаз весь час змінюється, внаслідок чого еліпс весь час деформується. При істотно різних періодах фігури Ліссажу не спостерігаються, оскільки еліпс деформується швидко, картина розмивається. Однак, якщо періоди відносяться як цілі числа, то через проміжок часу, рівний найменшому кратному обох періодів, точка, що рухається, знову повертається в те ж положення — виходять фігури Ліссажу складнішої форми. Фігури Ліссажу вписуються в прямокутник, центр якого збігається з початком координат, а сторони паралельні осям координат і розташовані по обидва боки від них на відстанях, рівних амплітудами коливань. При цьому кількість дотиків фігури до сторін прямокутника, в який вона вписана дає відношення періодів двох коливань.
де A,B — амплітуди коливань,a,b — частоти,δ — зсув фаз.
Вигляд кривої сильно залежить від співвідношення a/b. Коли співвідношення дорівнює 1, фігура Ліссажу має вигляд еліпсу, за певних умов вона має вигляд кола (A = B, δ = π/2 радіан) і лінії (δ = 0). Інший приклад фігури Ліссажу — парабола (a/b = 2, δ = π/2). Інші співвідношення продукують складніші фігури, які є замкненими за умови a/b — раціональне число. Припускається, що візуальна форма цих кривих є часто тривимірним вузлом, і насправді, проєкції на площину багатьох вузлів, включаючи вузли Ліссажу, є фігурами Ліссажу.
Фігури Ліссажу, де a = 1, b = N (N — натуральне число) і
є поліномами Чебишева першого роду степеня N.
Нижче наведені приклади фігур Ліссажу з δ = π/2, непарного натурального числа a, парного натурального числа b, і |a − b| = 1.
-
a = 1, b = 2 (1:2)
-
a = 3, b = 2 (3:2)
-
a = 3, b = 4 (3:4)
-
a = 5, b = 4 (5:4)
-
a = 5, b = 6 (5:6)
-
a = 9, b = 8 (9:8)
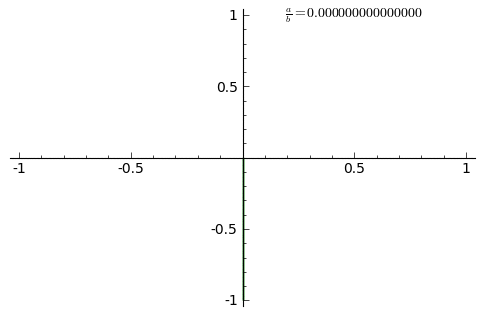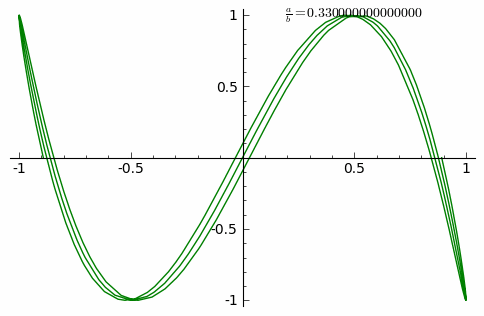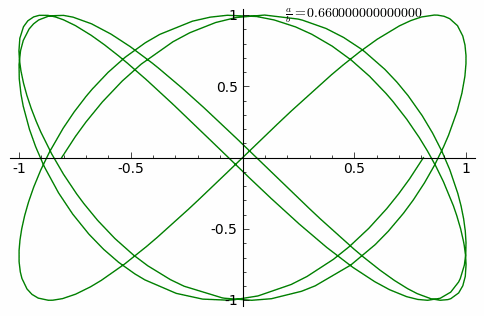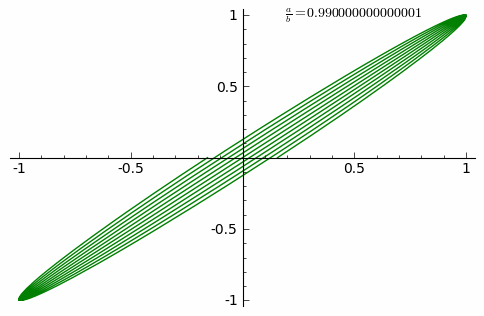
До початку періоду сучасної комп'ютерної графіки фігури Ліссажу зазвичай генерувались з допомогою спеціального механічного пристрою, що отримав назву гармонограф, пізніше — електронного осцилографа (на малюнку). Дві синусоїди, зсунуті по фазі, подавались на входи осцилоскопа в X-Y режимі і фазове взаємовідношення між сигналами являє собою фігуру Ліссажу.

Якщо подати на входи «X» і «Y» осцилографа сигнали кратних або рівних(близьких) частот, то на екрані можна побачити фігури Ліссажу. Цей метод широко використовується для порівняння частот і фаз двох джерел сигналів і для підлаштовування одного джерела під частоту іншого. Якщо коливання, які здійснює точка, відбуваються не за гармонійним, а за більш складним законом, але з однаковим періодом, то виходять замкнуті траєкторії, аналогічні фігурам Лісажу, але спотвореної форми. Коли частоти близькі, але не рівні одна одній, фігура на екрані обертається, причому період циклу обертання є величиною, оберненою різниці частот, наприклад, період обороту дорівнює 2с — різниця в частотах сигналів дорівнює 0,5 Гц. При рівності частот фігура застигає нерухомо, в будь-якій фазі, однак на практиці, за рахунок короткочасних нестабільностей сигналів, фігура на екрані осцилографа зазвичай трохи тремтить. Використовувати для порівняння можна не лише однакові частоти, але і ті, що знаходяться у кратному відношенні, наприклад, якщо зразкове джерело може видавати частоту тільки 5 МГц, а джерело, що налаштовуєтья — 2,5 МГц.
- Фігури Лісажу іноді використовуються в дизайні, як логотипи. Наприклад:
- Australian Broadcasting Corporation (a = 1, b = 3, δ = π/2)
- Лабораторія Лінкольна в MIT (a = 4, b = 3, δ = 0)[1]
- Університет електрокомунікацій, Японія (a = 3, b = 4, δ = π/2).
- ↑ Логотип Лабораторії Лінкольна. MIT Lincoln Laboratory. 2008. Архів оригіналу за 7 липня 2013. Процитовано 16 липня 2010.
- Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
- Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981
- гол.ред. А. М. Прохоров. Лиссажу фигуры Физическая энциклопедия. — Москва : "Советская энциклопедия", 1988. — Т. 2. — С. 597-598. — ISBN 5-85270-034-7.









