Еліпс

Еліпс утворений перетином конуса і нахиленої площини

Еліпс із фокусами

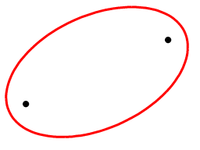
В геометрії, еліпс (від дав.-гр. ἔλλειψις (élleipsis) — «нестача», «упущення») — плоска замкнена алгебрична раціональна крива 2-го порядку без особливих точок.

Історично еліпс був означений як переріз прямого кругового конуса нахиленою площиною.

Назву «ἔλλειψις» (дав.-гр. ἔλλειψις — нестача, пропуск, випадіння (мається на увазі «неповнота» або «дефектність» еліпса порівняно з «повним» колом або кругом) кривій дав Аполлоній Перзький в своїй праці «Конічні перерізи».

В сучасній геометрії еліпс частіше означають як криву на площині, для кожної точки $P$ якої, сума відстаней до двох фіксованих точок $F_{1}$ та $F_{2}$ цієї площини (фокусів еліпса) є сталою величиною. А саме:

$PF_{1}+PF_{2}=2a.$

Окремим випадком еліпса є коло, в якого обидва фокуси збігаються в одній точці, що є центром цього кола.

Форма еліпса (ступінь його «витягнутості») визначається його ексцентриситетом — числом, що приймає будь-яке значення від 0 (граничний випадок для кола) до 1 (за винятком самої 1). Тобто еліпс є деформованим колом при його стисненні.

Еліпс — крива другого порядку, тобто в декартовій системі координат задається рівнянням другого степеня.

Еліпс є замкненим типом конічного перетину — двовимірною кривою, що утворюється внаслідок перетину прямого кругового конуса площиною (див. малюнок праворуч). Еліпси мають дуже багато спільного із іншими формами конічних перерізів: параболою і гіперболою, обидві з яких є відкритими і необмеженими кривими.

Перетином прямого кругового циліндра площиною також є еліпс, крім випадку, коли площина проходить паралельно осі обертання циліндра.

Еліпси широко використовуються в фізиці, астрономії та інженерії. Наприклад, орбіти планет нашої сонячної системи є дуже близькими до еліпсів, де однією із фокусних точок буде спільний барицентр планети і Сонця. Те саме є справедливим і для супутників, що обертаються довкола планет, і для інших систем, що складаються з двох астрономічних тіл. Форми планет і зірок часто добре описуються за допомогою еліпсоїдів.

Означення еліпса як геометричного місця точок

Еліпс: визначення

Еліпс можна визначити геометрично як множину точок (геометричне місце точок) у Евклідовому просторі:

• Еліпс — це множина точок, така, що для кожної точки $P$ цієї множини, сума відстаней $|PF_{1}|,\ |PF_{2}|$ до двох різних фіксованих точок $F_{1}$, $F_{2}$, що називаються фокусами, залишається сталою (зазвичай ця стала величина позначається як $2a,\ a>0$).
  

Для того, щоб виключити окремий випадок — лінійний відрізок, сталу величину $2a$ приймають більшою за відстань між точками $F_{1}$ та $F_{2}$:

$2a>|F_{1}F_{2}|.$

У більш формальному вигляді, для заданого $a$, еліпс є множиною

$E=\{P\in \mathbb {R} ^{2}\mid |PF_{2}|+|PF_{1}|=2a\}\ .$

Точки $F_{1}$ і $F_{2}$ називають фокусами еліпса.
Середню точку $O$ відрізку, що з'єднує між собою точки фокусів називають центром еліпса.
Відстань $c$ від фокуса до центра еліпса називають фокусною відстанню або лінійним ексцентриситетом. Отже, відстань між фокусами: $\left|F_{1}F_{2}\right|=2c$. Тоді за означенням маємо: $2a>2c,\ a>c$. Звідси можна сказати, що еліпс складається з таких і тільки таких точок $M$, які задовольняють умові: $\left|F_{1}M\right|+\left|F_{2}M\right|=2a$.

Пряма, що проходить через фокуси називається великою або головною віссю, а пряма, що проходить перпендикулярно до неї через центр називається малою віссю. На головній осі знаходяться вершини $V_{1},V_{2}$, відстань від яких до центра еліпса дорівнює $a$.

Відношення ${\frac {c}{a}}$ називають ексцентриситетом $e$ еліпса.

У випадку, коли $F_{1}=F_{2}$, еліпс приймає форму кола. Коло теж вважається еліпсом.

Еліпс: визначення із направляючим колом

Рівняння $|PF_{2}|+|PF_{1}|=2a$ можна розглянути в іншій формі (див. малюнок).

Якщо $c_{2}$ є колом із центром в точці $F_{2}$ і радіусом $2a$, тоді відстань від точки $P$ до кола $c_{2}$ дорівнює відстані до фокуса $F_{1}$:

$|PF_{1}|=|Pc_{2}|.$

$c_{2}$ називається круговою директрисою (що відноситься до фокуса $F_{2}$) еліпса. Цей випадок не треба плутати із визначенням еліпса за допомогою директриси, що є прямою лінією.

Інші означення еліпса

Еліпс в прямокутній системі координат

• Аналітичне означення
  Еліпсом називають лінію, яка в деякій декартовій прямокутній системі координат задається рівнянням:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Еліпс належить до кривих другого порядку.

• При розгляді куль Данделена можна довести наступне твердження:

Будь-який переріз прямого кругового конуса площиною, яка не проходить через вершину конуса і нахил якої менший ніж нахил твірних конуса до його основи, є еліпсом.

• Еліпс є перерізом прямого кругового циліндра похилою площиною;
• Еліпс є фігурою, що отримана з кола шляхом афінного перетворення;
• Еліпс є отрогональною проєкцією кола на площину.

Елементи еліпса

Вершини еліпса

Точки $A,\;A_{1},\;B,\;B_{1}$ перетину еліпса з осями прямокутної системи координат, вибраної так щоб початок координат був серединою відрізка $\left|F_{1}F_{2}\right|$, а вісь $Ox$ збігалася з прямою $\left(F_{1}F_{2}\right)$, називають вершинами еліпса.

Осі еліпса

Відрізок $\left|AA_{1}\right|=2a$, що проходить через обидва фокуси $F_{1}$ і $F_{2}$, називають великою віссю еліпса, а перпендикулярний йому відрізок $\left|BB_{1}\right|=2b$, що перетинається з великою віссю в центрі еліпса $O$ — відповідно його малою віссю. Довжина цих відрізків відповідає умові $a^{2}-b^{2}=c^{2}$. Еліпс симетричний відносно своїх осей та центра.

Директриса та ексцентриситет

Число $e={c \over a}$ — це ексцентриситет еліпса, величина, що характеризує його витягнутість; для еліпса ${\boldsymbol {e}}<1$.
Прямі, що мають рівняння $x=-{a \over e}$ та $x={a \over e}$ називають директрисами еліпса. Ці прямі характерні тим, що відношення відстані між будь-якою точкою еліпса та найближчим фокусом до відстані від цієї точки до найближчої директриси є сталим і дорівнює ексцентриситету.

Зауважимо, що величинами, які характеризують еліпс, є велика і мала півосі $a$ і $b$, відстань $c$ від фокуса до центру, ексцентриситет $e$. Залежність між ними виражається формулами: $a^{2}=b^{2}+c^{2},\;e={c \over a}$.

Тому, щоб скласти рівняння еліпса, досить знати або півосі $a$ і $b$, або одну піввісь і ексцентриситет і т. д.

Якщо точки $F_{1}$ і $F_{2}$ збігаються, то еліпс стає колом радіуса $a$. При цьому $a=b,\;e=0$. Отже, коло є окремим випадком еліпса.

Фокальний параметр

Довжина відрізку, що є половиною хорди, яка проходить через один із фокусів еліпса перпендикулярно до великої осі називається фокальним параметром $p$. Фокальний параметр моджна визначити за формулою:

$p={\frac {b^{2}}{a}}.$

Фокальний параметр $p$ також можна розглядати як радіус кривини стичного кола у вершинах $(\pm a,0)$.

Означення еліпса на основі властивості директриси

Еліпс: властивість директриси

Дві прямі, що лежать на відстані $d={\frac {a^{2}}{c}}$ від центра еліпса і паралельні малій осі еліпса називаються директрисами еліпса (див. рисунок).

• Для довільної точки $P$, що лежить на еліпсі відношення відстані від неї до одного з фокусів і до відповідної директриси (як на малюнку) дорівнює значенню ексцентриситета:

${\frac {|PF_{1}|}{|Pl_{1}|}}={\frac {|PF_{2}|}{|Pl_{2}|}}=e={\frac {c}{a}}\ .$

Доведення для пари $F_{1},l_{1}$ випливає із твердження, що $|PF_{1}|^{2}=(x-c)^{2}+y^{2},\ |Pl_{1}|^{2}=(x-{\tfrac {a^{2}}{c}})^{2}$ і $y^{2}={\tfrac {b^{2}}{a^{2}}}x^{2}-b^{2}$ задовольняють наступному рівнянню

$|PF_{1}|^{2}-{\frac {c^{2}}{a^{2}}}|Pl_{1}|^{2}=0\ .$

Аналогічним чином доводиться і другий випадок.

Обернене твердження є також вірним і його можна використовувати для означення еліпса (у спосіб аналогічний означенню параболи):

• Для будь-якої точки $F$ (що є фокусом), будь-якої прямої $l$ (директриса), що не проходить через точку $F$ і будь-якого дійсного числа $e$ такого що $0<e<1$ геометричне місце точок, для яких відношення відстані до даної точки і до прямої дорівнює $e$

$E=\{P\mid {\frac {|PF|}{|Pl|}}=e\}$

є еліпсом.

Вибір значення $e=0$, що відповідає значенню ексцентриситета для кола, в даному контексті не дозволяється. Можна вважати, що директрисою кола є пряма на нескінченності.

Пучок кривих конічних перетинів із спільною вершиною і спільною хордою, що проходить крізь фокус

(Вибір значення $e=1$ приводить до утворення параболи, а якщо $e>1$, то гіперболи.)

Доведення

Нехай $F=(f,0),\ e>0$ і припустимо, що $(0,0)$ є точкою кривої.

Директриса $l$ задана рівнянням $x=-{\tfrac {f}{e}}$. Якщо $P=(x,y)$, рівняння $|PF|^{2}=e^{2}|Pl|^{2}$ утворює наступні рівняння

$(x-f)^{2}+y^{2}=e^{2}(x+{\tfrac {f}{e}})^{2}=(ex+f)^{2}$ і $x^{2}(e^{2}-1)+2xf(1+e)-y^{2}=0.$

Після заміни $p=f(1+e)$ отримаємо

• $x^{2}(e^{2}-1)+2px-y^{2}=0.$

Це є рівняння еліпса ($e<1$) або параболи ($e=1$) або гіперболи ($e>1$). Всі ці невироджені конічні перетини мають спільний початок у вершині (див. малюнок).

Якщо $e<1$, введемо нові параметри $a,b$ такі, що $1-e^{2}={\tfrac {b^{2}}{a^{2}}}$, та $p={\tfrac {b^{2}}{a}}$, тоді вищезгадане рівняння стає

${\tfrac {(x-a)^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\ ,$

що є рівнянням еліпса із центром $(a,0)$, а вісь x є великою віссю, а довжини великої і малої півосей дорівнюють відповідно $a$ та $b$.

Загальний випадок

Якщо фокусом є $F=(f_{1},f_{2})$, а директрисою є $ux+vy+w=0$ отримаємо наступне рівняння:

$\left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}=e^{2}\cdot {\frac {(ux+vy+w)^{2}}{u^{2}+v^{2}}}$

(У правій частині рівняння використана нормальна форма Гессе для прямої, щоб розрахувати відстань $|Pl|$.)

Рівняння еліпса у декартовій системі координат

параметри, що описують форму еліпса:
a: велика піввісь,
b: мала піввісь
c: лінійний ексцентриситет,
p: фокальний параметр еліпса.

Канонічне рівняння еліпса

Якщо в Декартовій системі координат задати еліпс таким чином, що початок координат знаходитиметься в центрі еліпса, вісь x лежатиме на великій осі і

фокуси є точками, що задані як $F_{1}=(c,0),\ F_{2}=(-c,0)$,

вершинами є точки $V_{1}=(a,0),\ V_{2}=(-a,0)$.

Для довільної точки $(x,y)$ відстань до фокусу $(c,0)$ становитиме ${\sqrt {(x-c)^{2}+y^{2}}}$, а до другого фокусу ${\sqrt {(x+c)^{2}+y^{2}}}$. Точка $(x,y)$ знаходиться на еліпсі, якщо для неї виконується наступна рівність:

${\sqrt {(x-c)^{2}+y^{2}}}+{\sqrt {(x+c)^{2}+y^{2}}}=2a\ .$

Піднесемо обидві частини рівняння до квадрату і використаємо рівність $b^{2}=a^{2}-c^{2}$, в результаті чого отримаємо рівняння еліпса:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Якщо розв'язати його для y, то рівняння матиме вигляд:

$y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}.$

Параметри, які визначають форму еліпса $a,\;b$ називаються великою і малою півосями еліпса. Точки $V_{3}=(0,b),\;V_{4}=(0,-b)$ є вершинами еліпса на малій півосі.

З цього рівняння випливає, що еліпс є симетричним відносно обох осей координат і таким чином є симетричним відносно початку координат.

Параметричне рівняння еліпса

Еліпс в полярній системі координат.

За допомогою тригонометричних функцій $\cos ,\sin$, параметричне представлення еліпса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ можна задати так:

$\left\{{\begin{matrix}x=a\cos \alpha \\y=b\sin \alpha \end{matrix}}\right.,$ де $0\leqslant \alpha <2\pi .$

Параметр $\alpha$ (в астрономії його називають ексцентричною аномалією) по суті не є кутом $(x(\alpha ),y(\alpha ))^{T}$ утвореним із віссю x (як показано на діаграмі праворуч). Аби зрозуміти інтерпретацію параметру $\alpha$ необхідно розглянути розділ про методи креслення еліпсів.

Нормальне рівняння еліпса

${\frac {(x-x_{0})^{2}}{a^{2}}}+{\frac {(y-y_{0})^{2}}{b^{2}}}=1$

Дотична

Довільно обрана пряма $g$ може перетинати еліпс у 0, 1 або 2 точках. У першому випадку така пряма називається зовнішньою прямою, у другому випадку дотичною і січною у третьому випадку. Через одну точку еліпса можна провести лише одну дотичну.

Дотична в точці $(x_{0},y_{0})$ еліпса $\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ має наступне рівняння координат:

• $\ {\frac {x_{0}}{a^{2}}}x+{\frac {y_{0}}{b^{2}}}y=1\;.$

Рівняння дотичної у векторній формі є наступним:

• $\ {\vec {x}}={\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}}+s\;{\begin{pmatrix}-y_{0}a^{2}\\x_{0}b^{2}\end{pmatrix}}\quad$ із$\quad s\in \mathbb {R} \ .$

Доведення: Нехай $(x_{0},y_{0})$ буде точкою еліпса, а $\;{\vec {x}}={\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}}+s\;{\begin{pmatrix}u\\v\end{pmatrix}}\;$ є векторним рівнянням прямої $g$ (що містить $(x_{0},y_{0})$). Якщо додати рівняння прямої у рівняння еліпса і відповідно $\;{\tfrac {x_{0}^{2}}{a^{2}}}+{\tfrac {y_{0}^{2}}{b^{2}}}=1\;$ отримаємо:

${\frac {(x_{0}+su)^{2}}{a^{2}}}+{\frac {(y_{0}+sv)^{2}}{b^{2}}}=1\ ,\quad \longrightarrow \quad 2s\;\left({\frac {x_{0}u}{a^{2}}}+{\frac {y_{0}v}{b^{2}}}\right)+s^{2}\;\left({\frac {u^{2}}{a^{2}}}+{\frac {v^{2}}{b^{2}}}\right)=0\ .$

У випадку, коли ${\tfrac {x_{0}}{a^{2}}}u+{\tfrac {y_{0}}{b^{2}}}v=0\;(1)$ пряма $g$ і еліпс мають лише одну спільну точку $(x_{0},y_{0})$ і $g$ є дотичною. Напрям дотичної є ортогональним вектору $({\tfrac {x_{0}}{a^{2}}},{\tfrac {y_{0}}{b^{2}}})^{T}$, що є вектором нормалі відносно дотичної, а дотична має рівняння $\;{\tfrac {x_{0}}{a^{2}}}x+{\tfrac {y_{0}}{b^{2}}}y=k\;$ із досі не відомим $k$. Оскільки $(x_{0},y_{0})$ знаходиться і на дотичній і на еліпсі, отримаємо $k=1$.

У випадку, коли ${\tfrac {x_{0}}{a^{2}}}u+{\tfrac {y_{0}}{b^{2}}}v\neq 0\;(2)$ пряма $g$ має другу спільну точку із еліпсом.

із допомогою рівняння (1) можна легко перевірити, що $\;(-y_{0}a^{2},x_{0}b^{2})^{T}\;$ є вектором дотичної у точці $(x_{0},y_{0})$, що доводить векторне рівняння.

Примітка: Якщо $(x_{0},y_{0})$ і $(u,v)$ є двома точками на еліпсі, такими що виконується рівняння $\;{\tfrac {x_{0}u}{a^{2}}}+{\tfrac {y_{0}v}{b^{2}}}=0\;$, тоді точки знаходяться на двох спряжених діаметрах еліпса. У випадку коли $a=b$ еліпс є колом, а «спряженість» означатиме «ортогональність».

Нормаль є бісектрисою кута між прямими до точок фокусів

Еліпс: дотична до точки і нормаль, яка ділить навпіл кут між лініями до точок фокусів

промені із одного фокуса проходять через інший фокус

Для еліпса правдивим є наступне твердження:

• Нормаль, що проходить через точку $P$ є бісектрисою кута між прямими ${\overline {PF_{1}}},{\overline {PF_{2}}}$.

Доведення

Оскільки дотична є перпендикуляром до нормалі, твердження буде також вірним щодо дотичної і додаткових кутів до прямих, що проходять крізь фокуси (see diagram), too.

Нехай $L$ є точкою на прямій ${\overline {PF_{2}}}$, відстань від якої до фокусу $F_{2}$ дорівнює $2a$, $a$ є великою пів віссю еліпса. Пряма $w$ є бісектрисою кута між прямими ${\overline {PF_{1}}},{\overline {PF_{2}}}$. Для того, щоб довести що $w$ є дотичною прямою в точці $P$, перевіримо, що будь-яка точка $Q$ на прямій $w$, що є відмінною від точки $P$ не може знаходитися на еліпсі. Оскільки $w$ має одну єдину точку $P$ яка є спільною із еліпсом і є, таким чином, дотичною у точці $P$.

Із наведеного малюнку і нерівності трикутника можна встановити, що $2a=|LF_{2}|<|QF_{2}|+|QL|=|QF_{2}|+|QF_{1}|$ є вірним, що означає: $|QF_{2}|+|QF_{1}|>2a$. Але якщо $Q$ є точкою еліпса, сума повинна бути рівною $2a$.

Застосування

Промені, що проходять через один із фокусів відбиваються від кривої еліпса, так що вони проходять через другий фокус. Ця властивість має своє застосування у оптиці і акустиці, аналогічно як і аналогічна властивість відбивання променів у параболи (див. шепочуща галерея).

Діаметр еліпса

Спряжені діаметри еліпса (AB і CD).

Хордою еліпса називають відрізок, що сполучає дві точки еліпса.

Діаметром еліпса називають довільну хорду, що проходить через його центр. ^{:стор.88-89}

Також можливе означення діаметра еліпса (кола) — відрізок, що сполучає дві точки цього еліпса і проходить через його центр.

Діаметр, що відповідає хордам, паралельним малій осі еліпса, є його велика вісь, а діаметр, що відповідає хордам, паралельним великій осі, є мала вісь еліпса

Для еліпса ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ кутовий коефіціент $k$ паралельних хорд ($k\neq 0$) та кутовий коефіцієнт $k_{1}$ відповідного діаметра $y=k_{1}\cdot x$ пов'язані співвідношенням:

$k\cdot k_{1}=\varepsilon ^{2}-1=-{\frac {b^{2}}{a^{2}}}$

де $\varepsilon$ — ексцентриситет еліпса.

Спряженими діаметрами еліпса називають пару його діаметрів, що мають наступну властивість: середини хорд, паралельних першому діаметру, лежать на другому діаметрі. Тобто, діаметр еліпса ділить навпіл хорди, що паралельні до спряженого діаметра.

Два діаметри, спряжені один з одним і водночас взаємно перпендикулярні, називаються головними діаметрами. Вони є малою та великою осями еліпса та співпадають з його осями симетрії.

У кола кожен діаметр — головний. У еліпса, відмінного від кола, є лише одна пара головних діаметрів — велика і мала осі.

При обертанні діаметра його спряжений діаметр обертається у той самий бік.

Якщо еліпс є образом кола при афінному перетворенні, його спряжені діаметри є образами двох перпендикулярних діаметрів цього кола.

Спряжені діаметри і середні точки паралельних хорд

Ортогональні діаметри кола із квадратом, що утворений дотичними і показані середні точки паралельних хорд. Праворуч від кола афінне перетворення, що в результаті є еліпсом із спряженими діаметрами, паралелограмом із дотичних і середні точки хорд

Для кола вірною є наступна властивість:

(M) середні точки паралельних хорд знаходяться на діаметрі.

Діаметр і паралельні хорди є ортогональними. У загальному випадку афінне перетворення не зберігає ортогональність, але воно зберігає паралельність і середні точки лінійних відрізків. Звідси: властивість (M) (в якій пропущено термін ортогональність) є вірним для еліпса.

Визначення

Два діаметри $d_{1},\;d_{2}$ еліпса є спряженими якщо середні точки хорд, які є паралельними до $d_{1}$ лежать на $d_{2}.$

Із наведеної діаграми бачимо:

(T) Два діаметри $d_{1}={\overline {P_{1}Q_{1}}},d_{2}={\overline {P_{2}Q_{2}}}$, еліпса є спряженими, якщо дотичні в точках $P_{1}$ і $Q_{1}$ є паралельними до $d_{2}$ і навпаки.

Термін спряжені діаметри є свого роду узагальненням ортогональності.

Розглянемо параметричне рівняння:

${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t$

еліпса, будь-яка пара ${\vec {p}}(t),\ {\vec {p}}(t+\pi )$ точок належить діаметру, а пара ${\vec {p}}(t+\pi /2),\ {\vec {p}}(t-\pi /2)$ належить спряженому діаметру.

Метричні властивості

Нехай еліпс задано рівнянням:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$.

Тоді:

Площа

Площа $S$ області, що обмежена еліпсом, дорівнює:

$S=\pi \cdot ab$

де $a$ та $b$ — довжини великої і малої півосей, відповідно.

Формула площі $\pi \cdot ab$ є інтуїтивно зрозумілою:
площа кола радіусом $b$ дорівнює $\pi b^{2}$; стиснемо його із коефіцієнтом $a/b$ так, щоб утворити еліпс. Таке стисненняння маштабує його площу із тим самим коефіцієнтом: $\pi \cdot b^{2}\cdot {\frac {a}{b}}=\pi \cdot ab.$

Формулу площі еліпса легко довести, використавши інтегрування. Запишемо рівняння (1) еліпса у явному виді: $y(x)=b{\sqrt {1-x^{2}/a^{2}}}.$ На проміжку $x\in [-a,a],$ ця функція описує верхню половину еліпса.
Тому площа еліпса дорівнює подвоєному інтегралу від функції $y(x)$ на проміжку $[-a,a]$:

${\begin{aligned}S&=2\cdot \int _{-a}^{a}b{\sqrt {1-x^{2}/a^{2}}}\,dx\\&={\frac {b}{a}}\int _{-a}^{a}2{\sqrt {a^{2}-x^{2}}}\,dx.\end{aligned}}$

Другий інтеграл дорівнює площі круга із радіусом $a$, а саме, $\pi \cdot a^{2}.$ Тому

$S={\frac {b}{a}}\cdot \pi a^{2}=\pi \cdot ab.$

Площа еліпса, що заданий загальним рівнянням $Ax^{2}+Bxy+Cy^{2}=1$ дорівнює:

$S={\frac {2\pi }{\sqrt {4AC-B^{2}}}}$.

Довжина дуги еліпса

Довжина дуги еліпса обчислюється за формулою:

$l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt.$

Використавши параметричний запис рівняння еліпса, отримуємо наступний вираз:

$l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,dt.$

Після заміни $b^{2}=a^{2}\left(1-e^{2}\right)$ вираз довжини дуги приймає остаточний вигляд:

$l=a\int \limits _{t_{1}}^{t_{2}}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt,\;\;\;e<1.$

Отриманий інтеграл належить до родини еліптичних інтегралів, які не виражаються у елементарних функціях, і зводиться до еліптичного інтегралу другого роду $E\left(t,e\right)$. Зокрема, периметр еліпса дорівнює:

$l=4a\int \limits _{0}^{\pi /2}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt=4aE(e)$,

де $E\left(e\right)$ — повний еліптичний інтеграл Лежандра другого роду.

Наближені формули периметра

YNOT: $L=4\cdot \left(a^{x}+b^{x}\right)^{\left(1/x\right)}$, де $x={\frac {ln2}{ln({\frac {\pi }{2}})}}$. Максимальна похибка цієї формули становить близько 0,3619 % при ексцентриситеті еліпса близько 0,979811 (відношення осей ~1/5). Похибка завжди додатна.

Дуже наближена формула: $L=\pi \cdot \left(a+b\right)$

Дотична

Рівняння дотичної до еліпса через точку $\left.M_{0}\right.$(x₀;y₀), яка належить еліпсу

${\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.$

Методи креслення еліпсів

Центральна проєкція кіл (ворота)

Еліпси логічним чином виникають у нарисній геометрії як зображення (у паралельній чи центральній проєкції) кола. Тому дуже важливим є створення методів малювання еліпсів. До появи комп'ютерів, основними засобами для креслення були циркуль та лінійка, що використовувалися для побудови точок еліпса. А також існують інструменти (еліпсографи), які дозволяють малювати еліпси аналогічно, як циркулем малюють круги. Принцип роботи еліпсографа був відомий ще за часів давньогрецьких математиків (Архімеда, Прокла).

Якщо еліпсографа нема, найкращий і найшвидший спосіб — це намалювати еліпс з допомогою наближення за допомогою чотирьох кіл у вершинах еліпса.

Для використання будь-якого з наведених далі методів необхідно знати велику і малу осі еліпса (або: фокуси і велику піввісь). У випадку, якщо ця вимога не виконується, необхідно знати принаймні два його спряжені діаметри. Тоді за допомогою метода побудови Рітца можна знайти велику і малу осі.

Метод із канцелярськими кнопками і ниткою

Еліпс: Метод з ниткою і кнопками, або садовий метод

За визначенням еліпс є геометричним місцем точок для якого сума відстаней до фокусів є сталою. Це приводить до методу малювання із використанням двох канцелярських кнопок, нитки деякої довжини і олівця. За цим методом, кнопки закріплюються в двох точках, які є фокусами еліпса. Обидва кінці нитки закріплюються за допомогою цих двох кнопок кожний, а кінчик олівця відтягує нитку, так щоб утворився трикутник. Кінчик олівця буде окреслювати еліпс, якщо малювати фігуру так, щоб нитка була завжди натягнутою. Використовуючи цю техніку в саду, за допомогою кілків і мотузки, садівники таким чином розмічають еліптичні клумби, тому такий метод створення еліпсів іноді називають садовим.

За допомогою смужки паперу

Два наступних методи покладаються на параметричне представлення еліпса:

$(a\cos t,\;b\sin t)$

Це представлення можна змоделювати двома простими методами. В обох випадках необхідно знати велику і малу вісь $a,\;b$.

Метод 1

Перший метод починається з:

• маємо смужку з паперу довжиною $a+b$.

Точка, що розділяє довжини півосей позначена як $P$. Якщо смужка буде рухатися обома кінцями по осям бажаного еліпса, тоді точка P буде окреслювати еліпс. Для доказу покажемо точку $P$ у вигляді параметричного представлення $(a\cos t,\;b\sin t)$, де параметр $t$ є кутом нахилу паперової смужки.

Технічну реалізацію такого руху паперової смужки можна досягти за допомогою пристрою Тусі (див. анімацію). Цей пристрій дозволяє намалювати еліпс із фіксованою сумою $a+b$, що дорівнює радіусу більшого кола. Таке обмеження може бути недоліком для практичних задач. Більш гнучким є наступний метод.

Приклад: якщо хтось стоїть десь по середині сходів, які стоять на слизькій землі і опираються на слизьку стіну, така драбина почне ковзати вниз і ноги людини прослідують шляхом, що окреслює еліпс.

• 
  Побудова еліпса: метод 1 (за допомогою смужки паперу)
• 
  Еліпс за допомогою пристрою Тусі. Два приклади: червоний та блакитний.

Варіація методу 1 паперової смужки використовує спостереження, що середня точка $N$ паперової смужки рухається по колу із центром $M$ (еліпса) і радіусом ${\tfrac {a+b}{2}}$. Отже, паперову стрічку можна розрізати в точці $N$ на частини, що знову закріплюється з'єднанням в $N$ а рухомий кінець $K$ закріплюється в центрі $M$ (див. діаграму). Після цієї операції, рух незміненої частини стрічки залишається незмінним. Перевагою цього варіанту є те, що необхідно мати лише один ковзаючий елемент.

• 
  Варіація методу 1 (із паперовою смужкою)
• 
  Анімація варіації методу 1 (із паперовою смужкою)

Побудова еліпса: метод 2 (за допомогою смужки паперу)

Метод 2

Другий метод починається з:

• смужки паперу довжиною $a$.

Відмітимо точку, яка поділяє смужку на дві смужки, що мають довжини $b$ і $a-b$. Смужку розміщують на осі як показано на малюнку. Якщо смужку рухати, Тоді вільний кінець смужки буде окреслювати еліпс. Аби довести це, аналогічно можна описати точки, по яким рухається стрічка параметричним способом $(a\cos t,\;b\sin t)$, де параметр $t$ є кутом нахилу паперової смужки.

Цей метод лягає в основі декількох еліпсографів.

Примітка: Аналогічно до варіації із методом 1, інший варіант для другого методу із паперовою стрічкою можна отримати, якщо розрізати частину між двома осями на дві половини (див. діаграму).

• 
  Еліпсограф архімеда (принцип)
• 
  Еліпсограф Бенджаміна Брамера
• 
  Варіант методу 2 (із паперовою смужкою)

Наближення за допомогою кіл

Наближене креслення еліпса за допомогою кіл

Із метричних властивостей еліпса відомо, що:

• Радіус кола у вершинах $V_{1},V_{2}$ еліпса дорівнює: ${\tfrac {b^{2}}{a}}\ ,$

радіус кола у двох інших вершинах $V_{3},V_{4}$ становить: ${\tfrac {a^{2}}{b}}\ .$

На малюнку показано простий спосіб знаходження центрів $C_{1}=(a-{\tfrac {b^{2}}{a}},0),\;C_{3}=(0,b-{\tfrac {a^{2}}{b}})$ кола у вершинах $V_{1}$ і $V_{3}$, відповідно:

(1) відмітимо допоміжну точку $H=(a,b)$ і намалюємо відрізок $V_{1}V_{3}\ ,$

(2) намалюємо пряму через $H$, що є перпендикуляром до прямої $V_{1}V_{2}\ ,$

(3) точки перетину цієї прямої із віссю є центрами дотичних до еліпса кіл.

Центри для решти вершин можна знайти за допомогою симетрії.

Далі за допомогою лекала можна намалювати криву, яка плавно сполучаться із цими дотичними колами.

Генерування еліпса методом Штейнера

Еліпс: метод Штейнера

Еліпс: метод Штейнера

Наступний метод описує спосіб побудови окремих точок еліпса на основі генерації не вироджених конічних перетинів методом Штейнера:

• Маємо два пучки $B(U),B(V)$ прямих ліній, що виходять із двох точок $U,V$ (усі ці лінії містять $U$ або $V$, відповідно) і проективне, але не перспективне відображення $\pi$ пучка $B(U)$ у $B(V)$, тоді точки перетину відповідних прямих утворюють не вироджений конічний перетин.

Для генерації точок еліпса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ застосовують пучки, які виходять із вершин $V_{1},V_{2}$. Нехай $P=(0,b)$ є верхньою вершиною на малій осі еліпса і $A=(-a,2b),B=(a,2b)$. $P$ є центром прямокутника $V_{1},V_{2},B,A$. Сторону ${\overline {AB}}$ прямокутника поділено на однакові прямі відрізки і цей поділ проектується паралельно за допомогою діагоналі $AV_{2}$ на лінійний відрізок ${\overline {V_{1}B}}$, як це показано на малюнку. Паралельне проектування і обернення орієнтації є частиною необхідного проективного відображення між пучками в $V_{1}$ і $V_{2}$. Точка перетину будь-яких відповідних прямих $V_{1}B_{i}$ і $V_{2}A_{i}$ є точками, які однозначно задають еліпс. За допомогою цих точок $C_{1},\dotsc$ можна визначити точки другої чверті еліпса. Аналогічно можна отримати точки нижньої половини еліпса.

Примітки:

1. Генерація методом Штейнера існує також і для гіпербол і парабол.
2. Генерація Штейнера іноді називається методом паралелограма оскільки можна використати інші точки, а не вершити, які починаються з паралелограма, а не прямокутника.

Застосування

Фізика

Еліптичні рефлектори і акустика

Якщо в еліптичному резервуарі з водою поверхню води порушити в одному із його фокусів, кругові хвилі що утворяться, після відбиття від стінок, будуть збігатися одночасно в одну точку: другий фокус. Це є наслідком того, що загальна довжина будь-якого пройденого шляху між двома фокусами буде однаковою при відбитті від стінок.

Так само, якщо джерело світла розміщене в одному із фокусів еліптичного дзеркала, всі промені світла, що потрапляють на лощину еліпса відбиваються в точку другого фокуса. Оскільки жодна з гладких кривих не має такої властивості, її можна використовувати як альтернативне визначення еліпса. (Особливим випадком є коло, для якого усі промені із джерелом у центрі кола будуть відбиватися назад у центр кола.) Якщо еліпс обертати довкола його головної осі, що дозволяє отримати еліпсоїдальне дзеркало (зокрема, еліпсоїд обертання), ця властивість зберігається для всіх променів, що надходять з джерела. Як альтернативу, можна використати циліндричне дзеркало із еліптичним поперечним перерізом для того, щоб сфокусувати світло від прямої люмінесцентної лампи здовж прямої лінії на папері; такі дзеркала використовуються в деяких сканерах документів.

Звукові хвилі відбиваються аналогічним чином, тому у великій еліптичній кімнаті одна людина, знаходячись в одному із фокусів зможе надзвичайно добре чути іншу людину, що знаходиться в іншому фокусі. Цей ефект навіть більш відчутний під дахом із куполом, що має в основі форми має частину витягнутого сфероїда. Такі кімнати називають шепочущими галереями. Той самий ефект можна продемонструвати розмістивши на відповідній відстані два рефлектори, що мають форму кінців такого сфероїду. Прикладами таких споруджень є зал із скульптурами у Вашингтонському Капітолії (в якому, як кажуть, Джон Квінсі Адамс використовував цю властивість для підслуховування політичних розмов).

Планетарні орбіти

В 17-му столітті, Йоганн Кеплер відкрив, що орбіти по яким рухаються планети довкола Сонця є еліпсами, і Сонце знаходиться приблизно в одному із фокусів еліпса. Це відкриття називається першим законом планетарного руху. Згодом, Ісаак Ньютон пояснив це як наслідок свого закону всесвітнього тяжіння.

У загальному випадку, в рамках гравітаційної задачі двох тіл, якщо два тіла зв'язані одне з одним (так що, їх загальна енергія є негативною), їхніми орбітами будуть подібні еліпси із спільним барицентром, що буде знаходитися в одному їх фокусів кожного еліпса. Інші фокуси двох еліпсів не мають відомого фізичного значення. Цікаво, орбіта одного тіла в системі відліку другого тіла також буде еліпсом, де друге тіло знаходиться в тому ж фокусі.

Кеплерові еліптичні орбіти є результатом радіально спрямованої сили тяжіння, сила якої буде зворотньопропорційна квадрату відстані. Таким чином, в теорії, рух двох заряджених частинок у вільному просторі також буде здійснюватися по еліпсу. (Однак, таке припущення не бере до уваги втрати енергії через електромагнітного випромінення і квантових ефектів, що стають важливими при русі частинок на великій швидкості.)

Для еліптичних орбіт, корисними рівняннями, що пов'язані із ексцентриситетом $e$ є:

${\begin{aligned}e&={\frac {r_{a}-r_{p}}{r_{a}+r_{p}}}={\frac {r_{a}-r_{p}}{2a}}\\r_{a}&=(1+e)a\\r_{p}&=(1-e)a\end{aligned}}$

де

• $r_{a}$ є радіусом в апоцентрі (найбільша відстань)
• $r_{p}$ є радіусом в перицентрі (найменша відстань)
• $a$ це довжина великої півосі

Також, в термінах of $r_{a}$ і $r_{p}$, велика піввісь $a$ буде їхнім арифметичним середнім, мала піввісь $b$ буде їхнім геометричним середнім, а половина хорди фокусу еліпса $l$ дорівнює їх гармонійному середньому. Іншими словами,

${\begin{aligned}a&={\frac {r_{a}+r_{p}}{2}}\\b&={\sqrt {r_{a}\cdot r_{p}}}\\l&={\frac {2}{{\frac {1}{r_{a}}}+{\frac {1}{r_{p}}}}}={\frac {2r_{a}r_{p}}{r_{a}+r_{p}}}\end{aligned}}$.

Візуалізація фази сигналів

В електроніці, відносну фазу двох синусоїдних сигналів можна порівняти, якщо подати ці сигнали на вертикальний і горизонтальний входи осцилографа. Якщо на дисплеї буде видно еліпс, а не пряма лінія, два сигнали не в одній фазі.

Еліптичні коліщата

Два не круглих зубчатих колеса із однаковим еліптичним контуром, кожне з яких обертається довкола фокусу і розміщені під певним кутом, обертатимуться плавно зберігаючи контакт одне з одним. Альтернативним чином, вони можуть бути з'єднані ланцюгом або зубчастий ремінь, а у велосипеді основна ведуча зірка може мати еліптичну форму, або форму овалу подібного до еліпса. Такі еліптичні коліщата застосовують у механіці для того, щоб створити змінну кутову швидкість або момент сили при сталому обертанні привідної осі, або у випадку з велосипедом для того, щоб створити різну швидкість обертання кривошипа при оберненій зміні механічної переваги.

Еліптичні велосипедні шестерні полегшують рух ланцюга, коли його необхідно зняти при переключені передач.

Прикладом застосування такого механізму може бути пристрій, який намотує нитку на конічну котушку у прядильній машині. Котушку необхідно обертати швидше, коли нитка знаходиться біля вершини ніж, коли вона біля розширеної основи.

Оптика

У оптично анізотропному матеріалі (подвійне заломлення світла), показник заломлення залежить від напрямку падіння світла. Цю залежність можна описати за допомогою індексного еліпсоїда. Якщо матеріал є оптично ізотропним, цей еліпсоїд стає сферою.

Комп'ютерна графіка

Функціонал малювання еліпса як графічного примітиву є загальним у стандартних графічних бібліотеках, таких як QuickDraw API, і Direct2D в системі Windows. Джек Брезенхем із IBM є найбільш відомим за винайдення двовимірних графічних примітивів, включаючи лінію і коло, із використанням лише швидких операцій над цілими числами, такі як додавання та ін. Піттевей розширив алгоритми Брезенхема від ліній до конічних кривих в 1967. Інше ефективне узагальнення в зображенні еліпсів було винайдено в 1984 Джеррі Ван Акеном.

Денні Коен в 1970 р. на конференції «Комп'ютерна графіка 1970» в Англії представив лінійний алгоритм для малювання еліпсів і кіл. В 1971, Л. Б. Сміт опублікував подібні алгоритми для всіх конічних перетинів і довів, що він має хороші властивості. Ці алгоритми потребують лише декілька множень і додавань для розрахунку кожного з векторів.

Див. також

• Еліпсограф
• Коло
• Гіпербола (математика)
• Парабола
• Еліпс похибок

Література

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)
• Золотий логарифм і його застосування. Еліпс і рівняння його довжини / Є. П. Устянич. — Л. : Каменяр, 2011. — 76 с. : іл. — (Математичні новинки). — Бібліогр.: с. 73-74 (27 назв). — ISBN 978-966-607-177-7
• Еліпс // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
• Еліпс // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 109-110. — 594 с.