Пряма

Червона та блакитна прямі мають однаковий кутовий коефіцієнт; червона та зелена прямі мають спільний перетин з віссю y.

Геометрія
Проєкція сфери на площину
Історія
Галузі Евклідова Сферична Неевклідова еліптична гіперболічна Синтетична Аналітична Алгебрична арифметична діофантова Геометрія чисел Диференціальна диференціальна топологія конформна ріманова псевдоріманова симплектична фінслерова групи Лі Скінченна Проєктивна
Положення Властивості Виміри Побудова за допомогою циркуля та лінійки Кут Крива Діагональ Ортогональність перпендикулярність Паралельність Вершина Конгруентність Подібність Симетрія
Без- / одновимірна Точка Пряма відрізок промінь Довжина
Двовимірна Площина Площа Многокутник Трикутник Висота Гіпотенуза Теорема Піфагора Паралелограм Квадрат Прямокутник Ромб Ромбоїд Чотирикутник Трапеція Дельтоїд прямокутний Коло Діаметр Окружність Площа круга
Тривимірна Об'єм Куб прямокутний паралелепіпед Циліндр Піраміда (геометрія) Сфера
Чотири- / більше-вимірів Тесеракт Гіперсфера
Видатні геометри Айда Ясуакі Аріабхата I Ібн аль-Хайсам Аполлоній Архімед Майкл Атія Янош Бояї Брамагупта Елі Жозеф Картан Гарольд Коксетер Декарт Евклід Ейлер Гаусс Громов Гільберт Хаям Кляйн Бояї Лобачевський Манава Мінковський Мінггату Паскаль Піфагор Парамешвара Пуанкаре Ріман Насир ад-Дін ат-Тусі Вірасена Ян Хуей Чжан Хен
Категорія • Портал

Пряма́ або пряма́ лінія — одне з основних понять геометрії, введене античними математиками для позначення прямих об'єктів (тобто без кривини) з несуттєвою шириною та глибиною. Прямі є ідеалізаціями таких об'єктів.

Евклід описує пряму, як лінію нескінченної довжини, яка розташована однаково по відношенню до будь-якої своєї точки. Він визначив набір постулатів, як основних властивостей, що приймаються без доведень, а вже з них робляться логічні доведення, які і утворюють всю геометрію, яка зараз називається Евклідовою геометрією. Починаючи з кінці 19 сторіччя в активному вжитку знаходяться й інші геометрії, такі як неевклідові геометрії, проективна та афінна геометрії.

В сучасній математиці, в якій є багато геометричних концепцій, поняття лінії здебільшого залежить від способу, яким геометрія описується. Наприклад, в аналітичній геометрії, пряма визначається як множина точок, координати яких задовольняють лінійне рівняння. В більш абстрактних концепціях, таких, як геометрія інцидентності, пряма може бути незалежним об'єктом, відмінним від тих точок, з яких вона складається.

При аксіоматичному опису геометрії, поняття прямої лінії зазвичай залишається невизначеним, приймається за одне з вихідних понять (так зване неозначуване поняття), яке лише опосередковано визначається аксіомами геометрії. Перевагою такого підходу є гнучкість у використанні такої геометрії. Так у диференціальній геометрії, пряму можна розуміти як геодезичну лінію (найкоротший шлях між двома точками), а в проективній геометрії пряма є двовимірним векторним простором (всі лінійні комбінації двох незалежних векторів). Така гнучкість корисна не тільки математикам, а й іншим. Наприклад, фізики можуть мислити шлях проходження світла, як пряму лінію.

Означення та опис

Всі означення, зрештою, є циркулярними за своєю природою, оскільки вони залежать від понять, які також повинні мати означення, і цей ланцюг залежностей не можна продовжувати нескінченності без повернення назад до початкової точки. Тому, аби уникнути такого зациклювання, певні поняття мають бути прийняті як такі, що не потребують означення. В геометрії, таким поняттям часто є поняття прямої, що є одним із фундаментальних понять. В тих випадках, коли пряма може бути визначеним поняттям, як у аналітичній геометрії, за фундаментальні поняття обираються якісь інші примітиви. Якщо поняття прямої є фундаментальним невизначеним поняттям, тоді поведінка і властивості прямої визначаються за допомогою аксіом, яким вона повинна задовольняти.

При спрощеному або неаксиоматичному трактуванні геометрії, поняття або фундаментальне означення може бути занадто абстрактним, для уявлення. В таких випадках наводять описання або ментальний образ цього первісного поняття, аби сформувати основу для вибудовування поняття, яке формально буде базуватися на (невизначених) аксіомах. Деякі автори можуть наводити таке описання замість означення, користуючись цим неформальним стилем представлення. Але ці визначення не є вірними, і не можуть використовуватися в формальних виведеннях тверджень. «Означення» прямої в в математичних трактатах Евкліда підпадає під цю категорію. Навіть, при розгляді певної системи геометрії (наприклад, Евклідової геометрії), між авторами не існує загальноприйнятої згоди, щодо того яким повинно бути неформальне описання прямої, і те що воно не повинно розглядатися формально.

Властивості прямої в евклідовій геометрії

• Через будь-яку точку можна провести нескінченно багато прямих.
• Через будь-які дві незбіжні точки можна провести єдину пряму.
• Дві незбіжні прямі на площині або перетинаються в єдиній точці, або є паралельними (випливає з попереднього). У тривимірному просторі існують три варіанти взаємного розташування двох прямих.
• У тривимірному просторі існують три варіанти взаємного розташування двох прямих:
  • прямі перетинаються;
  • прямі паралельні;
  • прямі мимобіжні.

Алгебричне визначення

Три графіки ліній — червона та синя мають однаковий нахил k, а червона та зелена мають однаковий зсув b.

Пряма лінія — алгебрична лінія першого порядку: у декартовій системі координат пряма лінія задається на площині рівнянням першого степеня (лінійне рівняння):

$ax+by+c=0$

де $a\,$, $b\,$, $c\,$ — деякі числа, при чому $a\,$ або $b\,$ повинне бути відмінне від нуля. Це рівняння — загальне рівняння прямої. Його також називають «стандартним».

Натомість, рівняння прямої, що випливає з попереднього має вигляд лінійної функції в явному виді:

$y=kx+b$.

Це рівняння також називають рівнянням прямої з кутовим коефіцієнтом.

Пряма (а також пара пересічних прямих) є виродженим прикладом конічного перетину.

Загальне рівняння прямої

Загальне рівняння прямої лінії на площині в декартових координатах:

$Ax+By+C=0,\,$

де $A,B$ та $C$ — довільні сталі, причому числа $A$ та $B$ не дорівнюють нулю одночасно.

При $A=0$ пряма паралельна осі $Ox$, при $B=0$ — паралельна осі $Oy$.

Вектор з координатами $(A,B)$ називається нормальним вектором і є перпендикулярним до даної прямої.

При $C=0$ пряма проходить через початок координат.

Також рівняння можна переписати у вигляді:

$A(x-x_{0})+B(y-y_{0})=0.$

Рівняння прямої з кутовим коефіцієнтом

Рівняння прямої лінії, що перетинає вісь $Oy$ у точці $(0,\;b)$ і утворює кут $\varphi$ з додатним напрямком осі $Ox$:

$y=kx+b,\quad k=\mathrm {tg} \,\varphi .$

Коефіцієнт $k$ називається кутовим коефіцієнтом прямої.

У цьому вигляді неможливо представити пряму, паралельну координатній осі (іноді в цьому випадку формально кажуть, що кутовий коефіцієнт стає нескінченним).

Отримання рівняння прямої у відрізках

Рівняння прямої у відрізках

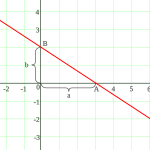
Рівняння прямої лінії, що перетинає вісь $Ox$ у точці $(a,\;0)$ та вісь $Oy$ у точці $(0,\;b)$:

${\frac {x}{a}}+{\frac {y}{b}}=1\quad (a\neq 0,\;b\neq 0).$

У цьому вигляді неможливо представити пряму, що проходить через початок координат.

Нормальне рівняння прямої

$x\cos \theta +y\sin \theta -p=0,\,$

де $p$ — довжина перпендикуляра, проведеного до прямої з початку координат, а $\theta$ — кут між нормальним до прямої вектором та додатним напрямом осі $Ox$. Якщо $p=0$, то пряма проходить через початок координат, а кут $\theta =\varphi +{\frac {\pi }{2}}$ задає кут нахилу прямої.

Якщо пряма задана загальним рівнянням $Ax+By+C=0,$ то відрізки $a$ та $b,$ що відсікаються нею на координатних осях, кутовий коефіцієнт $k,$ відстань до прямої від початку координат $p,$ $\cos \theta$ та $\sin \theta$  виражаються через коефіцієнти $A$, $B$ та $C$ наступним чином:

$a=-{\frac {C}{A}},\quad b=-{\frac {C}{B}},\quad k=\mathrm {tg} \,\varphi =-{\frac {A}{B}},\quad \varphi =\theta -{\frac {\pi }{2}},$

$p={\frac {C}{\pm {\sqrt {A^{2}+B^{2}}}}},\quad \cos \theta ={\frac {A}{\pm {\sqrt {A^{2}+B^{2}}}}},\quad \sin \theta ={\frac {B}{\pm {\sqrt {A^{2}+B^{2}}}}}.$

Щоб уникнути невизначеності, знак перед радикалом вибирається так, щоб дотримувалася умова $p>0.$ У цьому випадку $\cos \theta$ та $\sin \theta$ є напрямними косинусами нормалі прямої — перпендикуляра, проведеного з початку координат до прямої.

Якщо $C=0,$ то пряма проходить через початок координат і вибір позитивного напрямку довільний.

Рівняння прямої, що проходить через дві задані незбіжні точки

Якщо задано дві незбіжні точки з координатами $(x_{1},\;y_{1})$ та $(x_{2},\;y_{2})$, то пряма, що проходить через них задається рівнянням:

${\begin{vmatrix}x&y&1\\x_{1}&y_{1}&1\\x_{2}&y_{2}&1\end{vmatrix}}=0$

або

${\frac {y-y_{1}}{y_{2}-y_{1}}}={\frac {x-x_{1}}{x_{2}-x_{1}}}$

або у загальному вигляді

$\left(y_{1}-y_{2}\right)x+\left(x_{2}-x_{1}\right)y+\left(x_{1}y_{2}-x_{2}y_{1}\right)=0.$

Отримання векторного параметричного рівняння прямої

Векторне параметричне рівняння прямої

Векторне параметричне рівняння прямої задається вектором ${\vec {r}}_{0},$ кінець якого лежить на прямій, і напрямним вектором прямої ${\vec {u}}.$ Параметр $t$ пробігає всі дійсні значення.

${\vec {r}}={\vec {r_{0}}}+t{\vec {u}}.$

Параметричні рівняння прямої можуть бути записані у вигляді

${\begin{cases}x=x_{0}+a_{x}t,\\y=y_{0}+a_{y}t,\end{cases}}$

де $t$ — довільний параметр $a_{x},\;a_{y}$ — координати $x$ та $y$ напрямного вектора прямої. При цьому

$k={\frac {a_{y}}{a_{x}}},\quad a={\frac {a_{y}x_{0}-a_{x}y_{0}}{a_{y}}},\quad b={\frac {a_{x}y_{0}-a_{y}x_{0}}{a_{x}}},$

$p={\frac {a_{x}y_{0}-a_{y}x_{0}}{\pm {\sqrt {a_{x}^{2}+a_{y}^{2}}}}},\quad \cos \theta ={\frac {a_{x}}{\pm {\sqrt {a_{x}^{2}+a_{y}^{2}}}}},\quad \sin \theta ={\frac {a_{y}}{\pm {\sqrt {a_{x}^{2}+a_{y}^{2}}}}}.$

Сенс параметра $t$ аналогічний параметру в векторно-параметричному рівнянні.

Канонічне рівняння прямої

Канонічне рівняння виходить з параметричних рівнянь діленням одного рівняння на інше:

${\frac {x-x_{0}}{y-y_{0}}}={\frac {a_{x}}{a_{y}}}\Longleftrightarrow {\frac {x-x_{0}}{a_{x}}}={\frac {y-y_{0}}{a_{y}}}$

де $~a_{x},a_{y}$ — координати $~x$ та $~y$ напрямного вектора прямої, $~x_{0}$ та $~y_{0}$ координати точки, що належить прямій.

Рівняння прямої в полярних координатах $\rho$ та $\varphi$:

$\rho (A\cos \varphi +B\sin \varphi )+C=0$

або

$\rho \cos(\varphi -\theta )=p.\,$

Рівняння прямої у просторі

Векторне параметричне рівняння прямої в просторі:

${\vec {r}}={\vec {r}}_{0}+t{\vec {a}},\quad t\in (-\infty ,\;+\infty ),$

де ${\vec {r}}_{0}$ — радіус-вектор деякої фіксованої точки $M_{0},$ що лежить на прямій, ${\vec {a}}$ — ненульовий вектор, колінеарний цій прямій, ${\vec {r}}$ — радіус-вектор довільної точки прямої.

Параметричні рівняння прямої в просторі:

$x=x_{0}+t\alpha ,\;y=y_{0}+t\beta ,\;z=z_{0}+t\gamma ,\quad t\in (-\infty ,\;+\infty ),$

де $(x_{0},\;y_{0},\;z_{0})$ — координати фіксованої точки $M_{0},$ що лежить на прямій; $(\alpha ,\;\beta ,\;\gamma )$ — координати вектора, колінеарного цій прямій.

Канонічне рівняння прямої в просторі:

${\frac {x-x_{0}}{\alpha }}={\frac {y-y_{0}}{\beta }}={\frac {z-z_{0}}{\gamma }},$

де $(x_{0},\;y_{0},\;z_{0})$ — координати фіксованої точки $M_{0},$ що лежить на прямій; $(\alpha ,\;\beta ,\;\gamma )$ — координати вектора, колінеарного цій прямій.

Оскільки пряма є перетином двох різних площин заданих відповідно загальними рівняннями:

$({\vec {r}},\;{\vec {N}}_{1})+D_{1}=0$ і $({\vec {r}},\;{\vec {N}}_{2})+D_{2}=0,$

то рівняння прямої можна задати системою цих рівнянь:

${\begin{cases}({\vec {r}},\;{\vec {N}}_{1})+D_{1}=0,\\({\vec {r}},\;{\vec {N}}_{2})+D_{2}=0.\end{cases}}$

Векторне рівняння прямої в просторі :

Рівняння прямої в просторі можна записати у вигляді векторного добутку радіуса-вектора довільної точки цієї прямої ${\vec {r}}$ на фіксований вектор ${\vec {a}}$ прямої

$[{\vec {r}},{\vec {a}}]={\vec {M}},$

де фіксований вектор ${\vec {M}}$, ортогональний до вектора ${\vec {a}}$, можна знайти, підставляючи в це рівняння радіус-вектор якої-небудь однієї відомої точки прямої.

В n-вимірному просторі

Нехай задано вектор $k$ в n-вимірному Евклідовому просторі $E^{n}$, $k=(k_{i})\in E^{n}$, та $\alpha _{1},\dots ,\alpha _{n}$ — деякі фіксовані числа. Геометричне місце точок $x=x_{i}$ простору $E^{n}$, координати яких представлено у вигляді:

$x_{i}=k_{i}+\alpha _{i}t,\qquad -\infty <t<+\infty ,\quad i=1,\dots ,n$,

називається прямою в просторі $E^{n}$, що проходить через точку $k$ в «напрямі» $(\alpha _{1},\dots ,\alpha _{n})$.

Частина прямої, що відповідає зміні параметру $t$ в деякому відрізку $[a,b]$ називається прямолінійним відрізком, а її частина, що відповідає зміні параметру в проміжку $t\geq a$, — променем.

Якщо задано дві точки $(x'_{i})$, $(x''_{i})$ то рівняння прямої, що проходить через ці точки матиме вигляд:

$x_{i}=x'_{i}+(x''_{i}-x'_{i})t,\qquad -\infty <t<+\infty ,i=1,\dots ,n$.

Узагальнене визначення

• Прямою в афінному просторі ${\mathcal {A}}$ що задається точкою $M_{0}$ та відмінним від нуля вектором $\mathbf {a} \in {\mathcal {V}}$ називається множина точок $M$, для яких вектор ${\overrightarrow {M_{0}M}}$ колінеарний вектору $\mathbf {a}$, тобто, виконується рівність:

${\overrightarrow {M_{0}M}}=l\mathbf {a} .$

Таким чином, довільна пряма в просторі ${\mathcal {A}}$ має властивості афінного простору розмірності 1.

• В метричному просторі під «прямою» розуміють геодезичну лінію, тобто таку лінію, на якій досягається найменша відстань між двома точками.

Властивості

Пряма $m$ паралельна площині $\alpha$ тоді та лише тоді, коли в цій площині існує деяка пряма $p$ паралельна прямій $m$.

Якщо пряма $m$ паралельна кожній з площин $\alpha$ та $\beta$ що перетинаються, то вона паралельна лінії їхнього перетину.

Якщо три площини попарно перетинаються та не мають спільної прямої, то лінії їхнього перетину або паралельні або мають спільну точку.

В проективній геометрії

В багатьох моделях проективної геометрії, представлення прямої рідко відповідає поняттю «прямої лінії», як це є в Евклідовій геометрії. Типовий приклад цього, можна побачити в еліптичній геометрії. У випадку сферичного представлення еліптичної геометрії, прямі представлені як великі кола на сфері із визначеними на них діаметрально протилежними точками. У іншій моделі еліптичної геометрії, прямі задаються Евклідовими площинами, які проходять через початок системи координат. Хоча ці представлення візуально є відмінними, вони задовольняють властивостям проективної геометрії (наприклад, що дві точки визначають лише одну пряму), що роблять їх зручною відповідністю поняття прямої в цій геометрії.

Див. також

• Паралельні прямі
• Перпендикулярність прямих на площині
• Лінія Ейлера
• Лінійне рівняння
• Крива
• Кутовий коефіцієнт
• Гіперцикл (геометрія)
• Уявна пряма (математика)

Посилання

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)
• Пряма лінія на площині // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 88. — 594 с.
• Пряма лінія в просторі // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 134. — 594 с.